浙大数据结构第八周之08-图7 公路村村通

news2024/10/6 8:36:10

题目详情：

现有村落间道路的统计数据表中，列出了有可能建设成标准公路的若干条道路的成本，求使每个村落都有公路连通所需要的最低成本。

输入格式:

输入数据包括城镇数目正整数N（≤1000）和候选道路数目M（≤3N）；随后的M行对应M条道路，每行给出3个正整数，分别是该条道路直接连通的两个城镇的编号以及该道路改建的预算成本。为简单起见，城镇从1到N编号。

输出格式:

输出村村通需要的最低成本。如果输入数据不足以保证畅通，则输出−1，表示需要建设更多公路。

输入样例:

6 15
1 2 5
1 3 3
1 4 7
1 5 4
1 6 2
2 3 4
2 4 6
2 5 2
2 6 6
3 4 6
3 5 1
3 6 1
4 5 10
4 6 8
5 6 3

输出样例:

12

主要思路：

先补一下邻接表建图

邻接表的处理方法：

（1）图中顶点用一个一维数组存储，当然，顶点也可以用单链表来存储，不过，数组可以较容易的读取顶点的信息，更加方便。
（2）图中每个顶点vi的所有邻接点构成一个线性表，由于邻接点的个数不定，所以，用单链表存储，无向图称为顶点vi的边表，有向图则称为顶点vi作为弧尾的出边表。

例如，下图就是一个无向图的邻接表的结构：

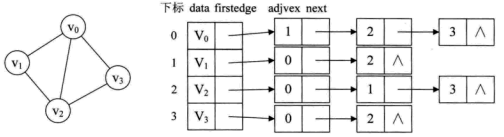
 从图中可以看出，顶点表的各个结点由data和firstedge两个域表示，

data是数据域，存储顶点的信息，

firstedge是指针域，指向边表的第一个结点，即此顶点的第一个邻接点。

边表结点由adjvex和next两个域组成。

adjvex是邻接点域，存储某顶点的邻接点在顶点表中的下标，（可以通过此下标在一维顶点数组中查询到这个顶点的信息）

next则存储指向边表中下一个结点的指针。


数据结构一：边：

typedef struct ENode *PtrToENode;
struct ENode{
    Vertex V1, V2;      /* 有向边<V1, V2> */
    WeightType Weight;  /* 权重 */
};
typedef PtrToENode Edge;

数据结构二：邻接点

/* 邻接点的定义 */
typedef struct AdjVNode *PtrToAdjVNode; 
struct AdjVNode{
    Vertex AdjV;        /* 邻接点下标 */
    WeightType Weight;  /* 边权重 */
    PtrToAdjVNode Next;    /* 指向下一个邻接点的指针 */
};

 数据结构三：顶点表头节点

/* 顶点表头结点的定义 */
typedef struct Vnode{
    PtrToAdjVNode FirstEdge;   /* 指向边表的第一个结点，即此顶点的第一个邻接点 */
    DataType Data;            /* 存顶点的数据 */
    /* 注意：很多情况下，顶点无数据，此时Data可以不用出现 */
} AdjList[MaxVertexNum];    /* AdjList是邻接表类型 */

数据结构四：图节点

/* 图结点的定义 */
typedef struct GNode *PtrToGNode;
struct GNode{  
    int Nv;     /* 顶点数 */
    int Ne;     /* 边数   */
    AdjList G;  /* 邻接表 */
};
typedef PtrToGNode LGraph; /* 以邻接表方式存储的图类型 */

初始化有顶点没有边的空图：

LGraph CreateGraph( int VertexNum )
{ /* 初始化一个有VertexNum个顶点但没有边的图 */
    Vertex V;
    LGraph Graph;
    
    Graph = (LGraph)malloc( sizeof(struct GNode) ); /* 建立图 */
    Graph->Nv = VertexNum;
    Graph->Ne = 0;
    /* 初始化邻接表头指针 */
    /* 注意：这里默认顶点编号从0开始，到(Graph->Nv - 1) */
       for (V=0; V<Graph->Nv; V++)
        Graph->G[V].FirstEdge = NULL;   //将每个顶点的邻接链表的头结点指针设置为 NULL。
            
    return Graph; 
}

插入边（插入的时候是头插法）

void InsertEdge( LGraph Graph, Edge E )
{    
    /* 插入边 <V1, V2> */
    /* 为V2建立新的邻接点 */
    PtrToAdjVNode NewNode = (PtrToAdjVNode)malloc(sizeof(struct AdjVNode));
    NewNode->AdjV = E->V2;
    NewNode->Weight = E->Weight;
    /* 将V2插入V1的表头，插入的边表示从v1指向v2 */
    NewNode->Next = Graph->G[E->V1].FirstEdge;
    Graph->G[E->V1].FirstEdge = NewNode;
        
    /* 若是无向图，还要插入边 <V2, V1> */
    /* 为V1建立新的邻接点 */
    NewNode = (PtrToAdjVNode)malloc(sizeof(struct AdjVNode));
    NewNode->AdjV = E->V1;
    NewNode->Weight = E->Weight;
    /* 将V1插入V2的表头 */
    NewNode->Next = Graph->G[E->V2].FirstEdge;
    Graph->G[E->V2].FirstEdge = NewNode;
}

建图 

LGraph BuildGraph()
{
    LGraph Graph;
    Edge E;
    Vertex V;
    int Nv, i;
    
    scanf("%d", &Nv);   /* 读入顶点个数 */
    Graph = CreateGraph(Nv); /* 初始化有Nv个顶点但没有边的图 */ 
    
    scanf("%d", &(Graph->Ne));   /* 读入边数 */
    if ( Graph->Ne != 0 ) { /* 如果有边 */ 
        E = (Edge)malloc( sizeof(struct ENode) ); /* 建立边结点 */ 
        /* 读入边，格式为"起点 终点 权重"，插入邻接矩阵 */
        for (i=0; i<Graph->Ne; i++) {
            scanf("%d %d %d", &E->V1, &E->V2, &E->Weight); 
            /* 注意：如果权重不是整型，Weight的读入格式要改 */
            InsertEdge( Graph, E );
        }
    } 

    /* 如果顶点有数据的话，读入数据 */
    for (V=0; V<Graph->Nv; V++) 
        scanf(" %c", &(Graph->G[V].Data));

    return Graph;
}

然后是Prim算法：

/* 邻接矩阵存储 - Prim最小生成树算法 */

Vertex FindMinDist( MGraph Graph, WeightType dist[] )
{ /* 返回未被收录顶点中dist最小者 */
    Vertex MinV, V; 
    WeightType MinDist = INFINITY;

    for (V=0; V<Graph->Nv; V++) {
        if ( dist[V]!=0 && dist[V]<MinDist) {
            /* 若V未被收录，且dist[V]更小 */
            MinDist = dist[V]; /* 更新最小距离 */
            MinV = V; /* 更新对应顶点 */
        }
    }
    if (MinDist < INFINITY) /* 若找到最小dist */
        return MinV; /* 返回对应的顶点下标 */
    else return ERROR;  /* 若这样的顶点不存在，返回-1作为标记 */
}

int Prim( MGraph Graph, LGraph MST )
{ /* 将最小生成树保存为邻接表存储的图MST，返回最小权重和 */
    WeightType dist[MaxVertexNum], TotalWeight;
    Vertex parent[MaxVertexNum], V, W;
    int VCount;
    Edge E;
    
    /* 初始化。默认初始点下标是0 */
       for (V=0; V<Graph->Nv; V++) {
        /* 这里假设若V到W没有直接的边，则Graph->G[V][W]定义为INFINITY */
           dist[V] = Graph->G[0][V];
           parent[V] = 0; /* 暂且定义所有顶点的父结点都是初始点0 */ 
    }
    TotalWeight = 0; /* 初始化权重和     */
    VCount = 0;      /* 初始化收录的顶点数 */
    /* 创建包含所有顶点但没有边的图。注意用邻接表版本 */
    MST = CreateGraph(Graph->Nv);
    E = (Edge)malloc( sizeof(struct ENode) ); /* 建立空的边结点 */
           
    /* 将初始点0收录进MST */
    dist[0] = 0;
    VCount ++;
    parent[0] = -1; /* 当前树根是0 */

    while (1) {
        V = FindMinDist( Graph, dist );
        /* V = 未被收录顶点中dist最小者 */
        if ( V==ERROR ) /* 若这样的V不存在 */
            break;   /* 算法结束 */
            
        /* 将V及相应的边<parent[V], V>收录进MST */
        E->V1 = parent[V];
        E->V2 = V;
        E->Weight = dist[V];
        InsertEdge( MST, E );
        TotalWeight += dist[V];
        dist[V] = 0;
        VCount++;
        
        for( W=0; W<Graph->Nv; W++ ) /* 对图中的每个顶点W */
            if ( dist[W]!=0 && Graph->G[V][W]<INFINITY ) {
            /* 若W是V的邻接点并且未被收录 */
                if ( Graph->G[V][W] < dist[W] ) {
                /* 若收录V使得dist[W]变小 */
                    dist[W] = Graph->G[V][W]; /* 更新dist[W] */
                    parent[W] = V; /* 更新树 */
                }
            }
    } /* while结束*/
    if ( VCount < Graph->Nv ) /* MST中收的顶点不到|V|个 */
       TotalWeight = ERROR;
    return TotalWeight;   /* 算法执行完毕，返回最小权重和或错误标记 */
}

其实本题可以只用邻接矩阵构建的图（或邻接表构建的图)也能解决，因为本题只要求MST的权值，并没有考察更多MST的性质，不过就当巩固所学吧 

代码实现：

#include <stdio.h>
#include <stdlib.h>
#define MAX_NODE_NUMS 1005
#define INFINITY 100000
#define TRUE 1
#define FALSE 0
#define NONE -1
#define ROOT 1
typedef int bool;
/*ListGraph的数据结构*/
/*边*/
typedef struct ENode ENode;
typedef ENode* PToEdgeNode;
struct ENode {
    int Start, End, Weight;
};
/*邻接点*/
typedef struct AdjVNode AdjVNode;
typedef AdjVNode* PToAdjVNode;
struct AdjVNode {
    int VertexIndex, Weight;
    PToAdjVNode Next;
};
/*头结点*/
typedef struct HeadNode HeadNode;
struct HeadNode {
    int Weight;
    PToAdjVNode FirstEdge;
};
/*图节点*/
typedef struct ListGraphNode ListGraphNode;
typedef ListGraphNode* ListGraph;
struct ListGraphNode {
    int EdgeNums, VertexNums;
    HeadNode AdjList[MAX_NODE_NUMS];
};
/*建一个空图*/
ListGraph CreateEmptyListGraph(int vertexNums) {
    ListGraph LGraph = (ListGraph)malloc(sizeof(ListGraphNode));
    LGraph->EdgeNums = 0; 
    LGraph->VertexNums = vertexNums;
    for(int i = 0; i <= vertexNums; i++) {
        LGraph->AdjList[i].FirstEdge = NULL;
    }
    return LGraph;
}
/*插入边*/
void InsertEdgeInLGraph(ListGraph LGraph, PToEdgeNode edge) {
    /*插入<start, end>的边*/
    PToAdjVNode newVertex = (PToAdjVNode)malloc(sizeof(AdjVNode));
    newVertex->VertexIndex = edge->End;
    newVertex->Weight = edge->Weight;
    newVertex->Next = LGraph->AdjList[edge->Start].FirstEdge;
    LGraph->AdjList[edge->Start].FirstEdge = newVertex;

    /*插入<end,start>的边，这是因为无向图，如果是有向图可以省略*/
    newVertex = (PToAdjVNode)malloc(sizeof(AdjVNode));
    newVertex->VertexIndex = edge->Start;
    newVertex->Weight = edge->Weight;
    newVertex->Next = LGraph->AdjList[edge->End].FirstEdge;
    LGraph->AdjList[edge->End].FirstEdge = newVertex;
    return;
}
ListGraph BuildListGraph(int vertexNums, int edgeNums) {
    ListGraph LGraph = CreateEmptyListGraph(vertexNums);
    for(int i = 0; i < edgeNums; i++) {
        PToEdgeNode newEdge = (PToEdgeNode)malloc(sizeof(ENode));
        scanf("%d %d %d", &(newEdge->Start), &(newEdge->End), &(newEdge->Weight));
        InsertEdgeInLGraph(LGraph, newEdge);
        free(newEdge);
    }
    return LGraph;
}

/*MatrixGraph的数据结构*/
typedef struct MatrixGraphNode MatrixGraphNode;
typedef MatrixGraphNode* MatrixGraph;
struct MatrixGraphNode {
    int VertexNums, EdgeNums;
    int Weight[MAX_NODE_NUMS][MAX_NODE_NUMS];
};
MatrixGraph CreateEmptyMatrixGraph(int vertexNums) {
    MatrixGraph MGraph = (MatrixGraph)malloc(sizeof(MatrixGraphNode));
    MGraph->VertexNums = vertexNums;
    MGraph->EdgeNums = 0;
    for(int i = 0; i <= vertexNums; i++) {
        for(int j = 0; j <= vertexNums; j++) {
            MGraph->Weight[i][j] = INFINITY;
        }
    }
    return MGraph;
}
void InsertEdgeInMGraph(int start, int end, int weight, MatrixGraph MGraph) {
    MGraph->Weight[start][end] = weight;
    MGraph->Weight[end][start] = weight;
    return;
}
MatrixGraph BuildMGraph(int vertexNums, int edgeNums) {
    MatrixGraph MGraph = CreateEmptyMatrixGraph(vertexNums);
    MGraph->EdgeNums = edgeNums;
    for(int i = 0; i < edgeNums; i++) {
        int start, end, weight;
        scanf("%d %d %d", &start, &end, &weight);
        InsertEdgeInMGraph(start, end, weight, MGraph);
    }
    return MGraph;
}
/*Prim算法*/
/*在剩余节点中找到与最小生成树权值最小的边*/
int FindMinDis(MatrixGraph MGraph, const int dis[]) {
    int minV = NONE;
    int minDist = INFINITY;
    for(int i = 1; i <= MGraph->VertexNums; i++) {
        if(dis[i] != FALSE && dis[i] < minDist) { //dist其实兼顾了Dijkstra中vis数组的作用
            minDist = dis[i];
            minV = i;
        }
    }
    return minV;
}
int Prim(MatrixGraph MGraph) {
    int dis[MAX_NODE_NUMS];     //dis[i]表示节点i到最小生成树的距离
    int parent[MAX_NODE_NUMS];
    int totalWeight = 0;
    int Vcount = 0;

    /*初始化dis和path数组，默认是从下标1开始，因为顶点从下标1开始*/
    for(int i = 1; i <= MGraph->VertexNums; i++) {
        dis[i] = MGraph->Weight[ROOT][i];  //由初始化可以看出，如果ROOT(定这个ROOT的原因是因为最小生成树只有一个根节点)~i两个节点之间有边，就初始化为权值，否则就初始化为INFINITY
        parent[i] = ROOT;    //假设所有顶点的上一级顶点都是ROOT
    }
    
    /*开始建立最小生成树*/
    ListGraph MST = CreateEmptyListGraph(MGraph->VertexNums);
    dis[ROOT] = 0;    //将顶点1作为最小生成树的根节点
    Vcount++;
    parent[ROOT] = NONE;

    while(TRUE) {
        int minV = FindMinDis(MGraph, dis);
        if(minV == NONE) break;
        /*将minV加入到最小生成树中*/
        PToEdgeNode newEdge = (PToEdgeNode)malloc(sizeof(ENode));
        newEdge->Start = parent[minV];
        newEdge->End = minV;
        newEdge->Weight = dis[minV];
        InsertEdgeInLGraph(MST, newEdge);
        Vcount++;
        totalWeight += dis[minV];
        dis[minV] = FALSE;    //防止重复加入

        /*更新dis和path数组*/
        for(int i = 1; i <= MGraph->VertexNums; i++) {
            if(dis[i] != FALSE && MGraph->Weight[minV][i] < INFINITY) {   //如果i是之前找到的最小顶点的邻接点并且没有收录
                if(dis[i] > MGraph->Weight[minV][i]) {  //如果收录最小的节点minV后使得节点i到最小生成树MST的距离变小
                    dis[i] = MGraph->Weight[minV][i];   
                    parent[i] = minV;
                }
            }
        }
        free(newEdge);
    }
    free(MST);
    if(Vcount < MGraph->VertexNums) return NONE;
    return totalWeight;
}
int main() {
    int vertexNums, edgeNums;
    scanf("%d %d", &vertexNums, &edgeNums);
    MatrixGraph MGraph = BuildMGraph(vertexNums, edgeNums);
    printf("%d", Prim(MGraph));
    free(MGraph);
    return 0;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/899060.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Linux 应急响应命令总结【持续更新】

Linux 应急响应命令总结【持续更新】

系统基本信息 CPU 信息 CPU 信息&#xff1a; lscpu操作系统信息 操作系统信息&#xff1a; uname -a操作系统信息&#xff1a; cat /proc/version模块信息 模块信息&#xff1a; lsmod账户信息 系统所有账户 系统所有账户&#xff1a; cat /etc/passwd超级权限账户…
阅读更多...
【leetcode 力扣刷题】快乐数/可被k整除的最小整数（可能存在无限循环的技巧题）

【leetcode 力扣刷题】快乐数/可被k整除的最小整数（可能存在无限循环的技巧题）

可能存在无限循环的技巧题 202. 快乐数数学分析 1015. 可被k整除的最小整数数学分析 202. 快乐数 题目链接&#xff1a;202. 快乐数 题目内容&#xff1a; 理解题意&#xff0c;快乐数就是重复每位数的平方之和得到的新数的过程&#xff0c;最终这个数能变成1。变成1以后&…
阅读更多...
STM32 串口复习

STM32 串口复习

按数据通信方式分类&#xff1a; 串行通信&#xff1a;数据逐位按顺序依次传输。传输速率较低&#xff0c;抗干扰能力较强&#xff0c;通信距离较长&#xff0c;I/O资源占用较少&#xff0c;成本较低。并行通信&#xff1a;数据各位通过多条线同时传输。 按数据传输方向分类&…
阅读更多...
04_Redis与mysql数据双写一致性案例

04_Redis与mysql数据双写一致性案例

04——redis与mysql数据双写一致性 一、canal 是什么 canal[ka’nel,中文翻译为水道/管道/沟渠/运河&#xff0c;主要用途是用于MySQL数据库增量日志数据的订阅、消费和解析&#xff0c;是阿里巴巴开发并开源的,采用Java语言开发&#xff1b; 历史背景是早期阿里巴巴因为杭州和…
阅读更多...
你知道CSGO转区内购吗？了解下内购系统！

你知道CSGO转区内购吗？了解下内购系统！

哈喽&#xff0c;大家好&#xff0c;我是童话姐姐&#xff0c;这两天群里很多人都在问关于内购的事情&#xff0c;今天就专门给大家讲一下关于内购的一些情况吧。 1、首先什么是转区内购? 顾名思义&#xff0c;内购就是在游戏内部的一个购买行为&#xff0c;csgo内购自然就是…
阅读更多...
MATLAB打开excel读取写入操作例程

MATLAB打开excel读取写入操作例程

本文使用素材含代码测试用例等 MATLAB读写excel文件历程含&#xff0c;内含有测试代码资源-CSDN文库 打开文件 使用uigetfile函数过滤非xlsx文件&#xff0c;找到需要读取的文件&#xff0c;首先判断文件是否存在&#xff0c;如果文件不存在&#xff0c;程序直接返回&#x…
阅读更多...
all in one之安装ubuntu-server系统（第二章）

all in one之安装ubuntu-server系统（第二章）

pve安装ubuntu-server系统 安装ubuntu-server系统 参考链接 在pve环境下安装ubuntu服务器版本&#xff0c;安装过程如下&#xff1a; ubuntu官方链接&#xff08;不推荐&#xff0c;下载慢&#xff09; 中科大开源库 阿里开源镜像库 兰州大学开源镜像站 … 自行选择进行下载&…
阅读更多...
韦东山-电子量产工具项目：页面系统

韦东山-电子量产工具项目：页面系统

代码结构 所有代码都已通过测试跑通&#xff0c;其中代码结构如下&#xff1a; 一、include文件夹 1.1 common.h #ifndef _COMMON_H #define _COMMON_Htypedef struct Region {int iLeftUpX; //区域左上方的坐标int iLeftUpY; //区域左下方的坐标int iWidth; //区域宽度…
阅读更多...
Nodejs沙箱逃逸--总结

Nodejs沙箱逃逸--总结

一、沙箱逃逸概念 JavaScript和Nodejs之间有什么区别&#xff1a;JavaScript用在浏览器前端&#xff0c;后来将Chrome中的v8引擎单独拿出来为JavaScript单独开发了一个运行环境&#xff0c;因此JavaScript也可以作为一门后端语言&#xff0c;写在后端&#xff08;服务端&#…
阅读更多...
Unity进阶–通过PhotonServer实现人物选择和多人同步–PhotonServer(四)

Unity进阶–通过PhotonServer实现人物选择和多人同步–PhotonServer(四)

文章目录 Unity进阶–通过PhotonServer实现人物选择和多人同步–PhotonServer(四)服务端客户端 Unity进阶–通过PhotonServer实现人物选择和多人同步–PhotonServer(四) 服务端 服务端结构如下&#xff1a; UserModel using System; using System.Collections.Generic; usin…
阅读更多...
houdini volume trail volume几种模式

houdini volume trail volume几种模式

1vdb from polygon 先 attribwrangle v 后vdbfrompolygon v 2 volume 3
阅读更多...
在 Transformer 之前生成文本 Text generation before transformers

在 Transformer 之前生成文本 Text generation before transformers

1. 在 Transformer 之前生成文本 重要的是要注意&#xff0c;生成算法并不是新的。先前的语言模型使用了一个叫做循环神经网络或RNN的架构。尽管RNN在其时代很强大&#xff0c;但由于需要大量的计算和内存来很好 地执行生成任务&#xff0c;所以它们的能力受到了限制。让我们看…
阅读更多...
好用的消售管理系统十大排行榜

好用的消售管理系统十大排行榜

销售管理是企业经营至关重要的一环。市场上有很多销售管理系统&#xff0c;对小企业来说&#xff0c;购买和实施CRM系统昂贵且复杂。这里有一份好用的10大免费销售管理系统榜单&#xff0c;让您既可以节省成本&#xff0c;又享受到高效的销售管理。 Zoho CRM&#xff1a; Zoh…
阅读更多...
Tesla Model S 3对比分析拆解图

Tesla Model S 3对比分析拆解图

文章来源&#xff1a;网络 需要特斯拉电驱样件的请&#xff1a;shbinzer &#xff08;拆车邦&#xff09; 5 款电机&#xff0c;其中扁线永磁同步电机最大功率从 202kW 提升至 220kW&#xff0c;最大扭矩从 404Nm提升至 440Nm。 Model S/X→Model 3/Y&#xff1a;双电机版本…
阅读更多...
软考A计划-系统集成项目管理工程师-收尾管理

软考A计划-系统集成项目管理工程师-收尾管理

点击跳转专栏>Unity3D特效百例点击跳转专栏>案例项目实战源码点击跳转专栏>游戏脚本-辅助自动化点击跳转专栏>Android控件全解手册点击跳转专栏>Scratch编程案例点击跳转>软考全系列点击跳转>蓝桥系列 &#x1f449;关于作者 专注于Android/Unity和各种游…
阅读更多...
2023河南萌新联赛第（五）场：郑州轻工业大学

2023河南萌新联赛第（五）场：郑州轻工业大学

A.买爱心气球 原题链接 : 登录—专业IT笔试面试备考平台_牛客网 博弈论 : #include <iostream> using namespace std; int t,n,m; string s1 "Alice",s2 "Bob"; int main() {cin>>t;while(t--){cin>>n>>m;if (n % 3 0) {cou…
阅读更多...
02_BigKey

02_BigKey

02——BigKey 一、MoreKey案例 大批量往redis里面插入2000w测试数据key 真实生产案例 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-LfbSfvNL-1692427337323)(https://you-blog.oss-accelerate.aliyuncs.com/2023/202303052248850.png)] 生产上严…
阅读更多...
购买steam余额有风险吗？以及N种被红锁的情况

购买steam余额有风险吗？以及N种被红锁的情况

购买steam余额有风险吗&#xff1f;以及N种被红锁的情况 无论是打游戏的玩家&#xff0c;还是像我们这类靠倒卖装备赚钱的小商贩&#xff0c;都面临充值美金余额的问题&#xff0c;我们现在主要是找的专业充值渠道做代充。 最近我发现群里有极个别学员通过自己的方法找到了一…
阅读更多...
Spring源码深度解析二(AOP)

Spring源码深度解析二(AOP)

书接上文 9. AOP源码深度剖析 概述 AOP&#xff08;Aspect Orient Programming&#xff09;&#xff1a;面向切面编程&#xff1b; 用途&#xff1a;用于系统中的横切关注点&#xff0c;比如日志管理&#xff0c;事务管理&#xff1b; 实现&#xff1a;利用代理模式&#x…
阅读更多...
【Java面试题】线程中start方法和run方法的区别？

【Java面试题】线程中start方法和run方法的区别？

start start作用是启动一个新线程。 当用start()开始一个线程后&#xff0c;线程就进入就绪状态&#xff0c;使线程所代表的虚拟处理机处于可运行状态&#xff0c;这意味着它可以由JVM调度并执行。但是这并不意味着线程就会立即运行。只有当CPU分配时间片时&#xff0c;这个线…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023