可能存在无限循环的技巧题
- 202. 快乐数
- 数学分析
- 1015. 可被k整除的最小整数
- 数学分析
202. 快乐数
题目链接：202. 快乐数
题目内容：
理解题意，快乐数就是重复每位数的平方之和得到的新数的过程，最终这个数能变成1。变成1以后，即便重复上述过程，也一直是1的循环，因此在重复得到新数的过程中，如果这个数等于1就停止。
问题：如果始终变不到1呢？题目中提到无限循环但始终变不到1，无限循环就意味着重复，如果重复找新数的过程中得到的数p在之前是出现过的，那么之后找到的数到下一次找到p前，都是重复出现的，直到变成p以后又继续循环。因此每次得到一个新数都要判断之前是否出现过，如果出现过就终止过程，返回false。
查找这个数是否出现过，用什么数据结构？ 哈希表！【快速查找一个元素是否存在】 用什么实现哈希表呢？前面的题目有用到数组、set和map。 对于此题，一个数n，将其每位数求平方再相加这个重复过程中会得到多少种数是不确定的，因此不能用数组；map存<key，value>此题我们不需要value，只需要key，因此直接用set。
每次得到一个新数首先判断其每位数平方之后是否为1，是直接返回true；如果不是再判断这个数是否已经出现在set中，如果是，直接返回false；如果不是重复寻找新数的过程并重复上述判断。
代码如下（C++）：
class Solution {
public:
//对整数n每位数求平方再相加求和的过程
int getsum(int n){
int sum = 0;
while(n){
sum+= (n%10) * (n%10);
n= n/10;
}
return sum;
}
bool isHappy(int n) {
//存出现过的数
unordered_set<int> count;
int sum = getsum(n);
//每位数平方和不等于1才进入循环，找新数
//如果等于1，即为快乐数
while(sum != 1){
//如果已经存在过，就进入循环了
if(count.count(sum))
return false;
else count.insert(sum);
//找新数
sum = getsum(sum);
}
return true;
}
};
数学分析
一个数不是快乐数，那么就进入无限循环，但是万一这个循环内的数字特别大特别多呢？
力扣这道题的官方题解中，分析了9，99，……，9999999等这些共i位数字的最大的情况，各位平方求和后的数字：
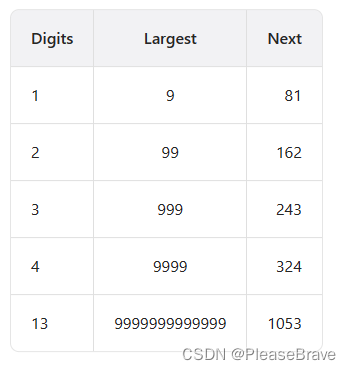
题目中n<=2^31-1，也就是2147483648-1，最多10的10次方，而只有13位的数字，其各位平方之和才能上千。就算各位数平方之和达到了四位数，再求和一次就变成了三位数，再求和一次就变成了243以内。因此再大的数字经过各位数平方求和操作后，大小都会迅速下降，最终控制在243以内，要么进行循环，要么最终变成1。
所以实际上用数组实现哈希表也是可以的，初始化数组长度为243，元素全是0。代码如下（C++）：
bool isHappy(int n) {
//用数组存出现过的数字
int count[243] = {0};
int sum = getsum(n);
//每位数平方和不等于1才进入循环，找新数
//如果等于1，即为快乐数
while(sum != 1){
//如果已经存在过，就进入循环了
if( sum<=243 && count[sum-1])
return false;
//注意控制下标不要越界
if( sum<= 243 )
count[sum-1]++;
//找新数
sum = getsum(sum);
}
return true;
}
1015. 可被k整除的最小整数
题目链接：1015. 可被k整除的最小整数
题目内容：
理解题意：①正整数需要满足：能够被k整除的【即n%k=0】，仅包含数字1【比如11，1111，111…111等】；②满足①中的条件的n可能不止一个，那么要找其中最小的；③返回n的长度而不是数字n本身。
如何表示这样的n？ 假设n初始化为1，然后逐渐增大n = n*10 + 1，直到找到n满足题意。但是这样的int类型的n最多只能有10位，继续增大n就超出了int类型的范围，即便是64位的带符号的整数（最大为18446744073709551616），n的长度也只有20。 因此不能直接用上式表示n，并且本题本身也不要求返回n而是n的长度。
解法
- 用余数r来代替n：
假设：n%k = r （即：n = k*i + r ，i≥1）
那么：n’%k = (n*10+1)%k = (k*i*10 +r*10 +1) %k = (r*10+1)%k
因此可以用 r*10+1代替n*10+1
并且因需要求出n的长度，不需要记录n，因此用余数r来代替n； - 如果无解就会出现循环，存在a>b（都是由数字1组成的），a%k = b%k ≠ 0，用哈希表（set）存出现过的余数，如果重复出现就表示进入循环无解：
【解法①】用哈希表存出现过的余数，如果再次出现说明进入循环无解：
class Solution {
public:
int smallestRepunitDivByK(int k) {
int res = 1 % k;
int len = 1;
//存出现过的余数
unordered_set <int> set_res;
//余数=0就不进入循环，直接返回结果
while(res){
//如果余数≠0且出现了重复，就直接返回
if(set_res.count(res))
return -1;
set_res.insert(res);
res = (res * 10 + 1) % k;
len++;
}
return len;
}
};
【优化】实际上余数r的范围是0~k-1，总共k个数字，那么如果有解，循环k次内，一定会找到结果：
class Solution {
public:
int smallestRepunitDivByK(int k) {
int res = 1%k, len = 1;
//最多循环k次
for(int i = 0 ;i < k ;i++){
if(!res) return len;
res = (res*10 + 1)%k;
len++;
}
return -1;
}
};
数学分析
- 能够直观的知道k是否有解？
如果k是2或者5的倍数，因为n是奇数肯定不能被2整除，因为n的末尾是1而不是0或者5，肯定不能被5整除。 - 除2和5以外的k一定有解吗？
假设有全是1的数字a和b对k同余，即a%k = b%k ，那么(a - b)%k = 0，而a - b = 11…1100…00，可以表示成a - b = (11…11)*(10^x)，k不等于2和5的倍数，即k和10是互质的，a-b能够整除k的话，只能是（11…11）能够整除k，11…11恰好全是由1构成的，即11…11就是解，因此k如果不是2和5的倍数，就一定有解。
代码实现（C++）：因为k除2和5的倍数外一定有解，那么就一直寻找就行，直到余数=0
int smallestRepunitDivByK(int k) {
//如果是2或者5的倍数无解直接返回-1
if(k%2==0||k%5==0) return -1;
//n=1，初始长度len=1
int len=1;
//r表示余数，初始n=1，r=n%k=1%k
int r=1%k;
//只要余数r不为0，就没有找到可以整除k的数，继续循环
while(r){
len++;
//末尾增加1
r=r*10+1;
//求余
r=r%k;
}
return len;
}
