1. 计算器问题

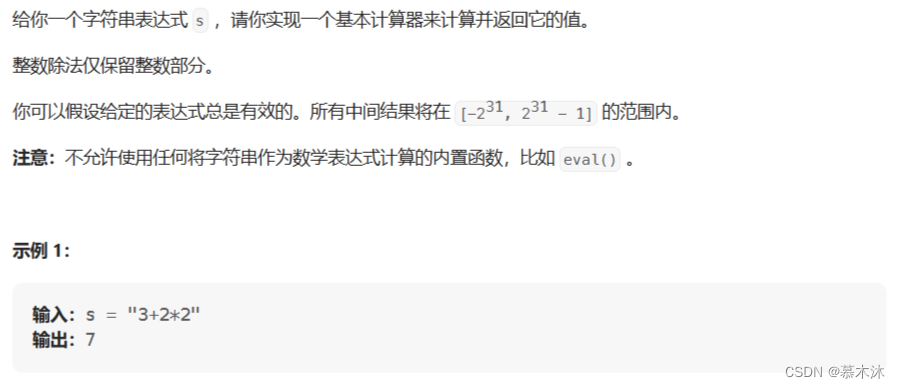
思路：此题不考虑括号和负数情况，单纯使用栈即可解决。注意的是数字可能是多位数需要保留完整的num， 保留数字的前缀符号，当碰到加号，存进去；当碰到减号，存相反数进去；当碰到乘除就弹出栈顶元素运算后把结果存进去；最后相加就是结果

class Solution {
    public int calculate(String s) {
        Deque<Integer> stack = new ArrayDeque<Integer>();
        char preSign = '+';
        int num = 0;
        int n = s.length();
        for (int i = 0; i < n; ++i) {
            char c = s.charAt(i);
            if(c >= '0' && c <= '9'){
                num = num*10 + c - '0';
            } 
            if((!(c >= '0' && c <= '9')&&c != ' ') || i==n-1 ){
                switch(preSign){
                    case '+' :
                        stack.push(num);
                        break;
                    case '-' :
                        stack.push(-num);
                        break;
                    case '/':
                        stack.push(stack.pop()/num);
                        break;
                    case '*':
                        stack.push(stack.pop()*num);
                        break;
                }
                preSign = c;
                num=0;
            }
        }
        num = 0;
        while(!stack.isEmpty()){
            num += stack.pop();
        }
        return num;
    }
}

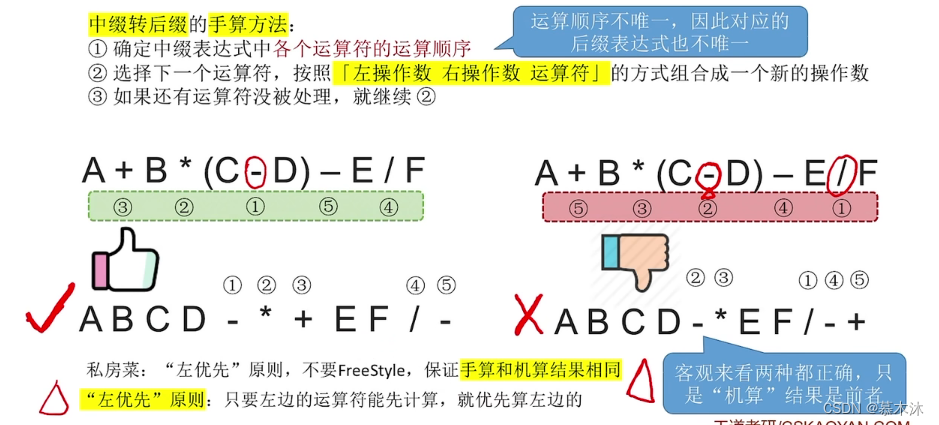
 2.逆波兰表达式

• 中缀表达式
  • 运算符在两个操作数中间
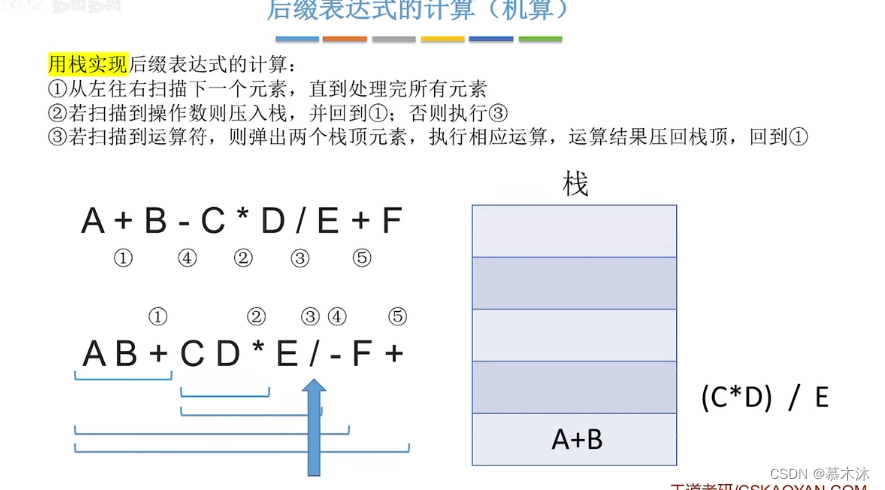
• 后缀表达式
  • 运算符在两个操作数后面
• 前缀表达式
  • 运算符在两个操作数前面

class Solution {
    public int evalRPN(String[] tokens) {
        Deque<Integer> stack = new LinkedList<>();
        for(int i = 0;i<tokens.length;i++){
            if(!Character.isDigit(tokens[i].charAt(0)) && tokens[i].length() == 1){
                 int num2 = stack.pop();
                int num1 = stack.pop();
                switch (tokens[i]) {
                    case "+":
                        stack.push(num1 + num2);
                        break;
                    case "-":
                        stack.push(num1 - num2);
                        break;
                    case "*":
                        stack.push(num1 * num2);
                        break;
                    case "/":
                        stack.push(num1 / num2);
                        break;
                    default:
                }
            }else{
                stack.push(Integer.parseInt(tokens[i]));
            }
        }
        return stack.pop();
    }
}