1 不同路径

题目：

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。

问总共有多少条不同的路径？

题解：
动态规划。想要计算[m - 1][n - 1]，需要计算[m - 2][n - 1]和[m - 1][n - 2]。从[0][0]开始递推即可。

class Solution {
public:
	int uniquePaths(int m, int n) {
		vector<vector<int>> results(m,vector<int>(n,1));
		for (int i = 1; i < m; i++) {
			for (int j = 1; j < n; j++) {
				results[i][j] = results[i - 1][j] + results[i][j - 1];
			}
		}
		return results[m - 1][n - 1];
	}
};

2 最长公共子序列

题目：

给定两个字符串 text1 和 text2，返回这两个字符串的最长 公共子序列 的长度。如果不存在
公共子序列 ，返回 0 。

一个字符串的 子序列 是指这样一个新的字符串：它是由原字符串在不改变字符的相对顺序的情
况下删除某些字符（也可以不删除任何字符）后组成的新字符串。

例如，"ace" 是 "abcde" 的子序列，但 "aec" 不是 "abcde" 的子序列。
两个字符串的 公共子序列 是这两个字符串所共同拥有的子序列。

题解：
动态规划。下图为官方的说明。
在这里插入图片描述

class Solution {
public:
    int longestCommonSubsequence(string text1, string text2) {
        int m = text1.length(), n = text2.length();
        vector<vector<int>> dp(m + 1, vector<int>(n + 1));
        for (int i = 1; i <= m; i++) {
            char c1 = text1.at(i - 1);
            for (int j = 1; j <= n; j++) {
                char c2 = text2.at(j - 1);
                if (c1 == c2) {
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                } else {
                    dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
                }
            }
        }
        return dp[m][n];
    }
};

3 买卖股票的最佳时机含手续费

题目：

给定一个整数数组 prices，其中 prices[i]表示第 i 天的股票价格 ；整数 fee 代表了
交易股票的手续费用。

你可以无限次地完成交易，但是你每笔交易都需要付手续费。如果你已经购买了一个股票，
在卖出它之前你就不能再继续购买股票了。

返回获得利润的最大值。
注意：这里的一笔交易指买入持有并卖出股票的整个过程，每笔交易你只需要为支付一次手续费。

题解：
贪心。将手续费计算在买入的时候。
当买入时，将价格prices[i]和费用fee求和存于buy。
如果遇到价格prices[j]+fee低于buy，则得买这一天的，更新下buy。
如果遇到价格prices[k]高于buy，则可以得卖出。但这个卖出的时刻不一定是最佳的，所以需要将prices[k]存入buy，如果遇到更大的prices[l]，则在这一天卖更好。

待证明的一点：如果遇到高于buy的prices[k]，然后再遇到prices[m],它小于prices[k]但大于prices[k]-fee，此时是未买入的，这是否合理？
证明：如下图两种情况。第一种：如果存在prices[m]，然后prices又继续往上升，则按算法逻辑会更新卖出时刻，改为在第二个峰值点卖出。第二种：如果存在prices[m]，然后就再也没有超过prices[k]的值，则再次买入是不合理的，因为不管怎么交易的价格差异都小于fee，赚不到钱。
在这里插入图片描述

class Solution {
public:
    int maxProfit(vector<int>& prices, int fee) {
        int n = prices.size();
        int buy = prices[0] + fee;
        int profit = 0;
        for (int i = 1; i < n; ++i) {
            if (prices[i] + fee < buy) {
                buy = prices[i] + fee;
            }
            else if (prices[i] > buy) {
                profit += prices[i] - buy;
                buy = prices[i];
            }
        }
        return profit;
    }
};

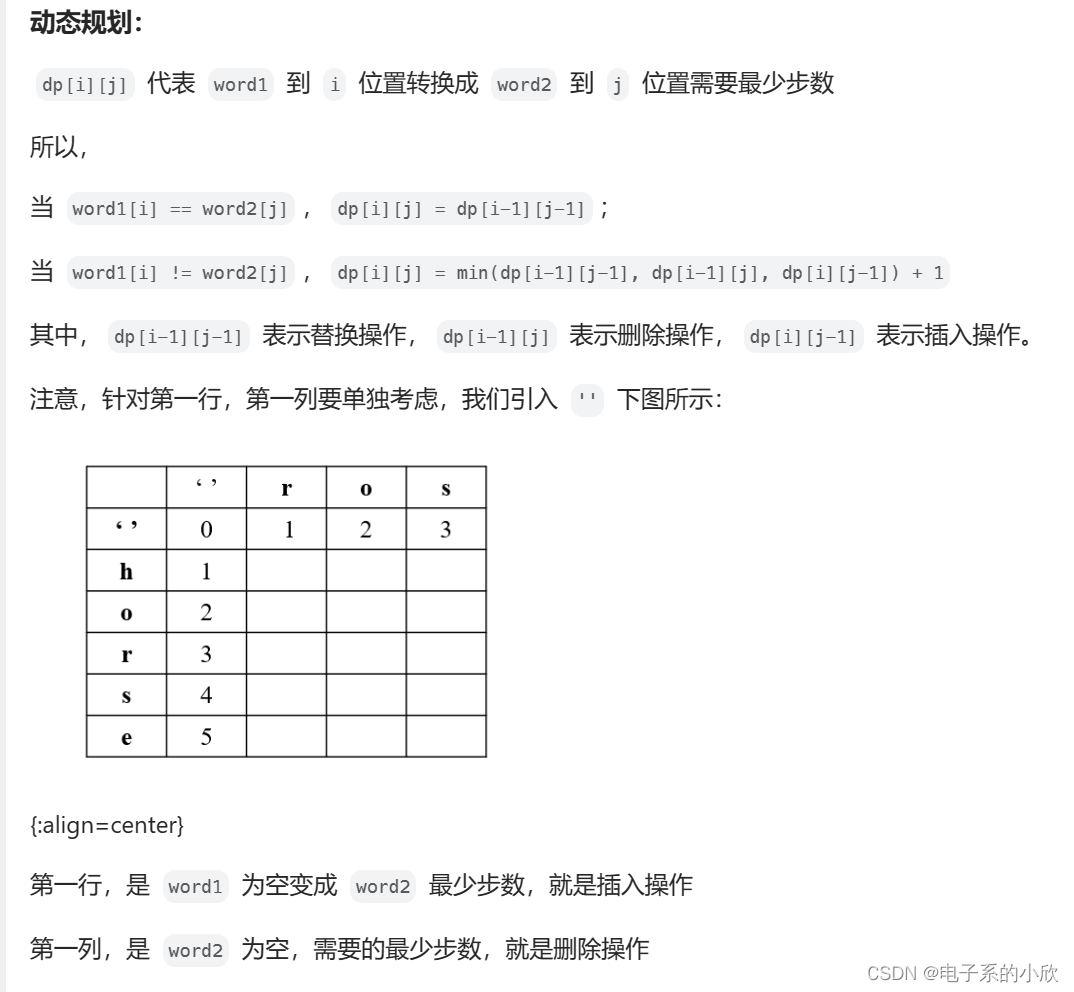
4 编辑距离

题目：

给你两个单词 word1 和 word2， 请返回将 word1 转换成 word2 所使用的最少操作数  。

你可以对一个单词进行如下三种操作：
插入一个字符
删除一个字符
替换一个字符

题解：
这道题的阶梯思路与题目2相似，但更困难，下图为评论区@自底向上和自顶向下的解释。
在这里插入图片描述

class Solution {
public:
    int minDistance(string word1, string word2) {
        int n = word1.length();
        int m = word2.length();

        // 有一个字符串为空串
        if (n * m == 0) return n + m;

        // DP 数组
        vector<vector<int>> D(n + 1, vector<int>(m + 1));

        // 边界状态初始化
        for (int i = 0; i < n + 1; i++) {
            D[i][0] = i;
        }
        for (int j = 0; j < m + 1; j++) {
            D[0][j] = j;
        }

        // 计算所有 DP 值
        for (int i = 1; i < n + 1; i++) {
            for (int j = 1; j < m + 1; j++) {
                int left = D[i - 1][j] + 1;//删除
                int down = D[i][j - 1] + 1;//插入
                int left_down = D[i - 1][j - 1];//修改
                if (word1[i - 1] != word2[j - 1]) left_down += 1;
                D[i][j] = min(left, min(down, left_down));

            }
        }
        return D[n][m];
    }
};