Vue渲染器（四）：双端diff算法

news2024/11/26 8:46:28

渲染器（四）：双端diff算法

在上一章中，我们介绍了简单diff算法的实现原理。它利用vnode的key属性，尽可能多地复用DOM，并通过移动DOM的方式来完成更新，从而减少不断地创建和销毁DOM元素带来的性能开销。但是仍然存在不少缺陷，接下来就介绍双端diff算法来解决。

1.双端比较的原理：

这里主要通过一个例子来说明原理，所以废话会比较多（不是）。如果原理已经了解的朋友，可以直接跳到这节的后面看结论和代码。

先看上一章的例子：

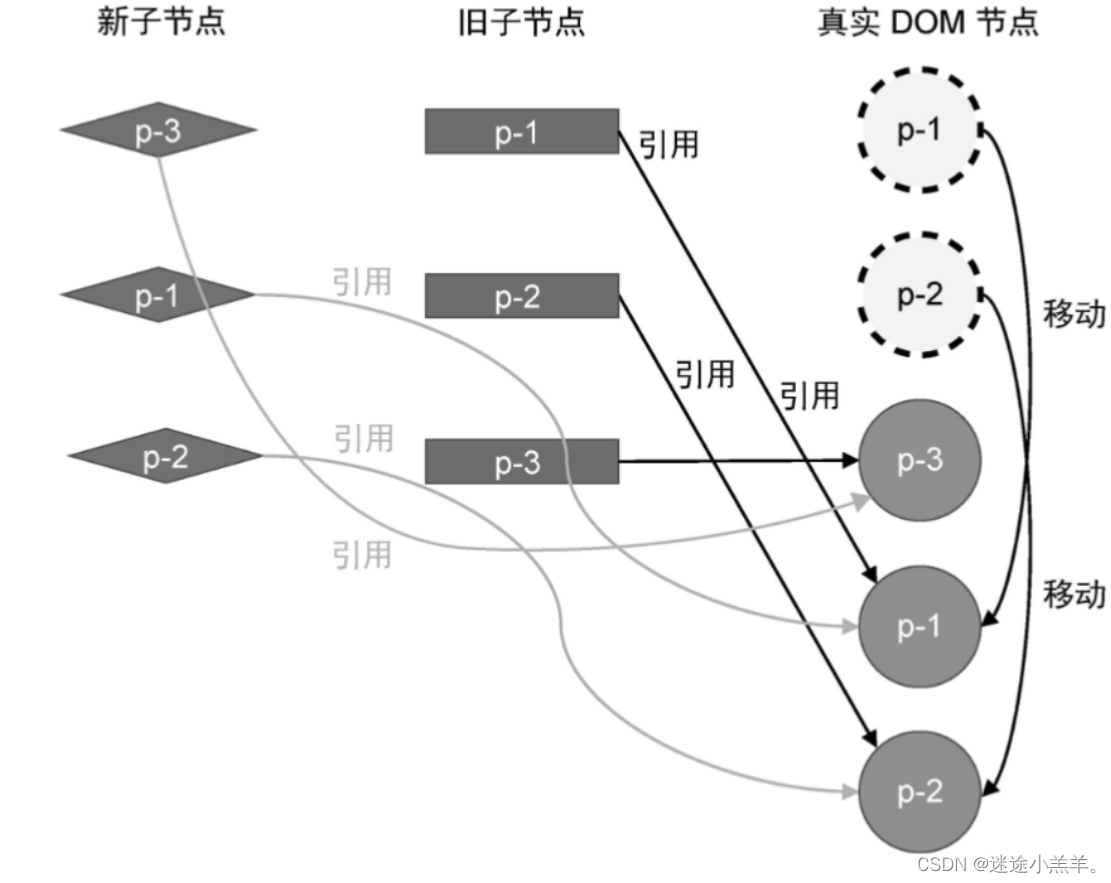
在这里插入图片描述

它会发生两次DOM移动操作来完成更新，但是它不是最优解，因为通过观察我们可以最优解应该是：把真实DOM节点 p-3移动到 真实DOM节点 p-1前面，这样就只需要一次DOM移动操作即可完成更新。
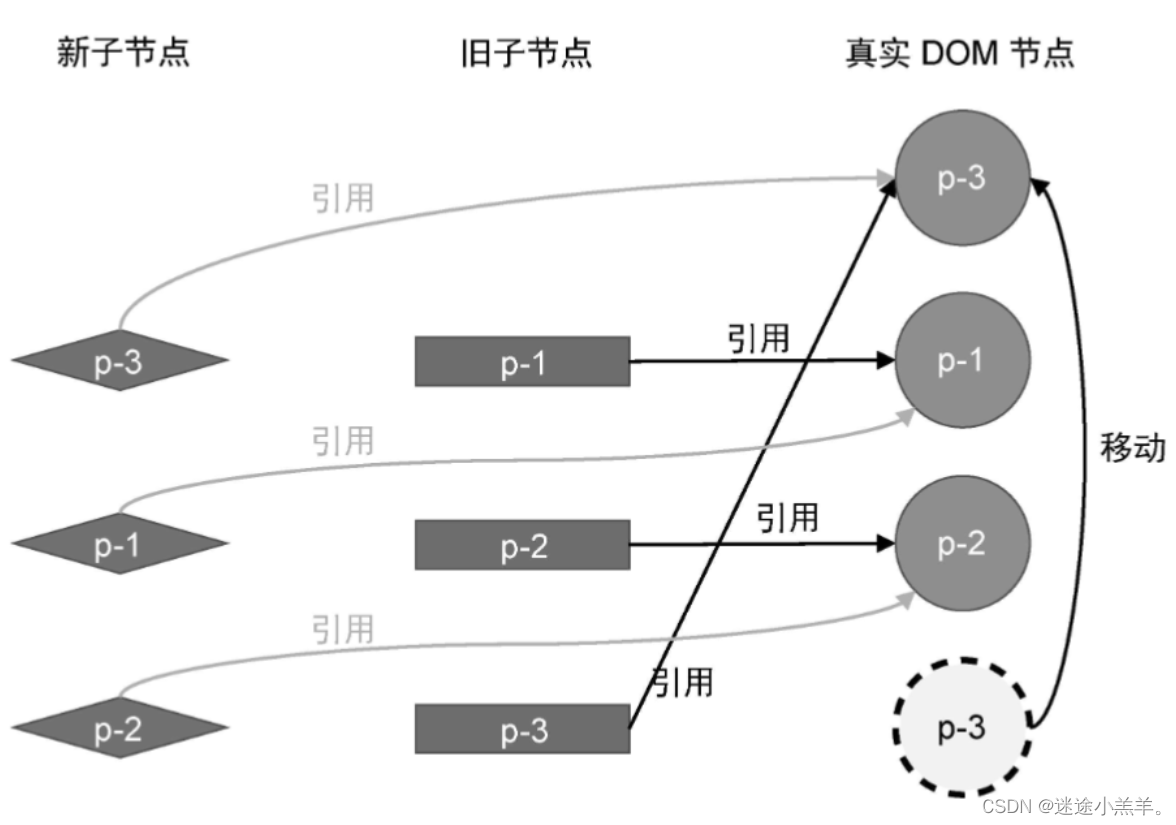
在这里插入图片描述

简单diff算法做不到这点，但是双端diff算法可以做到。接下来就让我们来认识下它。

先下定义：双端diff算法是一种同时对新旧vnode的两个端点进行比较的算法。它的优势在于比起简单Diff算法，可以减少DOM移动次数。

我们需要四个索引值，分别指引新旧vnode的端点，如图：
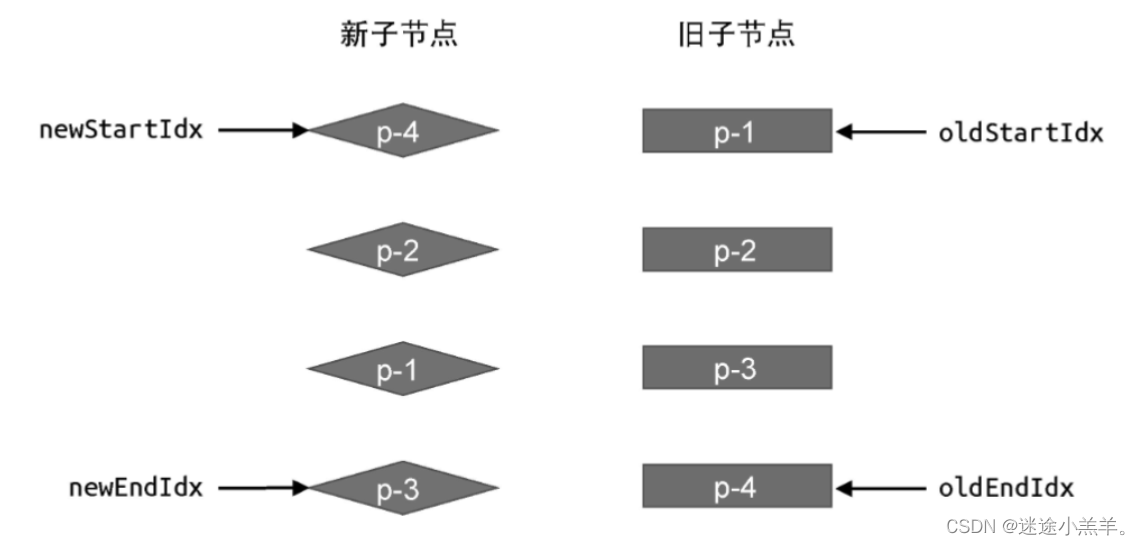
在这里插入图片描述

封装 patchKeyChildren函数：

function patchKeyedChildren(n1, n2, container) {
    const oldChildren = n1.children
    const newChildren = n2.children
    // 四个索引值 
    let oldStartIdx = 0
    let oldEndIdx = oldChildren.length - 1
    let newStartIdx = 0
    let newEndIdx = newChildren.length - 1
    // 四个索引指向的 vnode 节点 
    let oldStartVNode = oldChildren[oldStartIdx]
    let oldEndVNode = oldChildren[oldEndIdx]
    let newStartVNode = newChildren[newStartIdx]
    let newEndVNode = newChildren[newEndIdx]
}

有了这些后，就可以开始进行双端比较了。怎么比较呢？如下图所示：
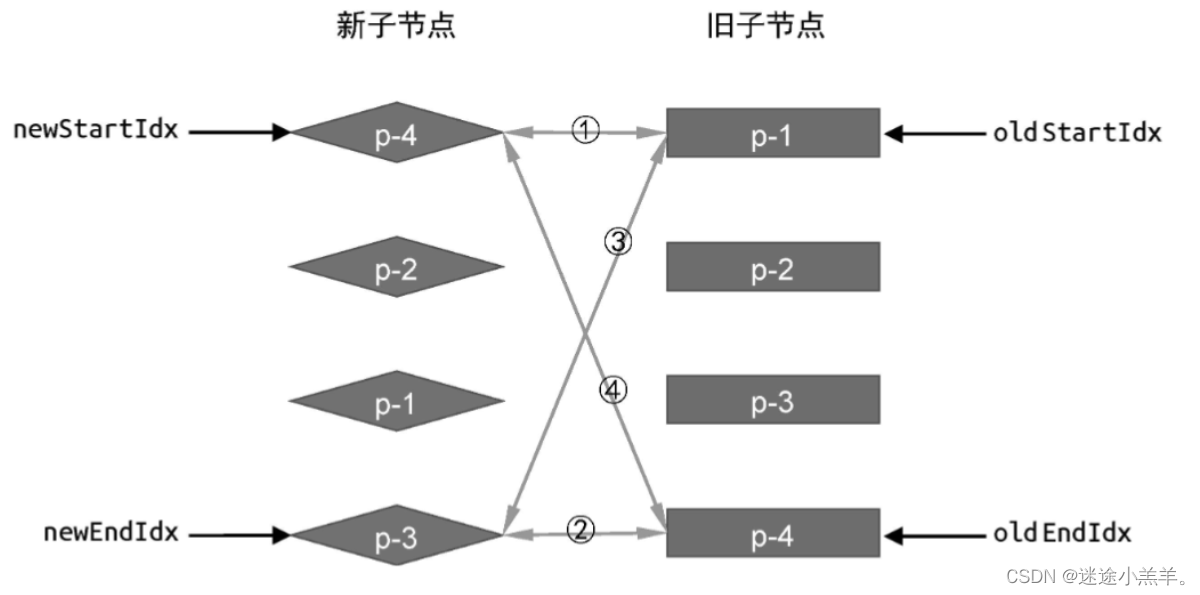
在这里插入图片描述

每一轮比较都分为四个步骤，如上图1234所示：

  • 第一步：比较旧vnode的第一个子节点p-1 和 新vnode的第一个子节点p-4，key值不同，所以什么也不做；
  • 第二步、第三步同上；
  • 第四步：比较旧vnode中的最后一个子节点p-4 和新vnode中的第一个子节点p-4，key相同，可以进行DOM复用。

可以看到，在第四步找到了相同节点，通过移动DOM元素来进行真实DOM节点的复用。那么该怎么复用呢？

观察一下，可以发现 旧vnode中p-4原本是最后一个子节点，在新vnode中变成了第一个子节点。对应到程序逻辑：将旧vnode的 oldEndIdx索引指向的vnode所对应的真实DOM，移动到索引 oldStartIdx指向的vnode所对应的真实DOM前面。如下代码：

function patchKeyedChildren(n1, n2, container) {
    const oldChildren = n1.children
    const newChildren = n2.children
    // 四个索引值 
    let oldStartIdx = 0
    let oldEndIdx = oldChildren.length - 1
    let newStartIdx = 0
    let newEndIdx = newChildren.length - 1
    // 四个索引指向的 vnode 节点 
    let oldStartVNode = oldChildren[oldStartIdx]
    let oldEndVNode = oldChildren[oldEndIdx]
    let newStartVNode = newChildren[newStartIdx]
    let newEndVNode = newChildren[newEndIdx]
    if (oldStartVNode.key === newStartVNode.key) {
        // 第一步比较
    } else if (oldEndVNode.key === newEndVNode.key) {
        // 第二步比较
    } else if (oldStartVNode.key === newEndVNode.key) {
        // 第三步比较
    } else if (oldEndVNode.key === newStartVNode.key) {
        // 第四步比较
        // 仍然调用patch函数进行打补丁
        patch(oldEndVNode, newStartVNode, container);
        // 移动DOM操作
        insert(oldEndVNode.el, container, oldStartVNode.el);
        // 移动DOM完成后,更新索引值,并指向下一个位置
        oldEndVNode = oldChildren[--oldEndIdx];
        newStartVNode = newChildren[++newStartIdx];
    }
}

在这段代码中，增加了一系列的 if...else if语句，用来实现四个索引指向的vnode之间的比较。但是我们只实现了第四步的，后面再慢慢完善。在第四步DOM移动操作完成后，新旧vnode以及真实DOM节点的状态如下图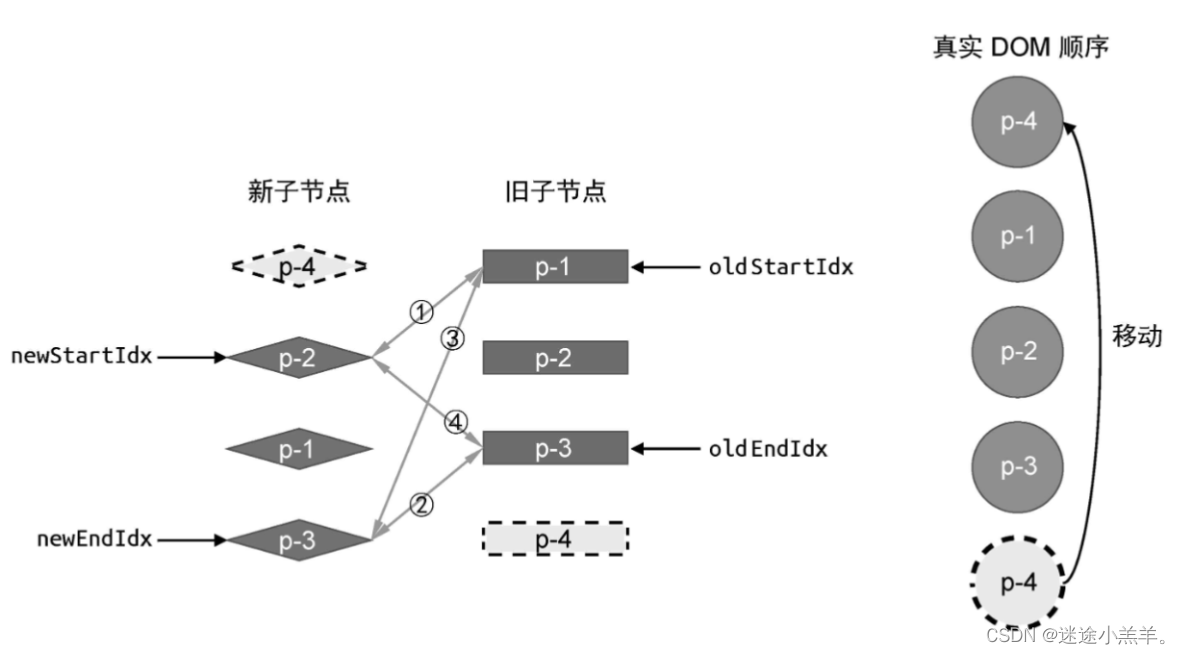：在这里插入图片描述

此时，真实DOM节点顺序为 p-4 、p-1、p-2、p-3，这与新vnode子节点顺序不同。因为diff算法还没有结束，还需要进行下一轮更新。因此将更新逻辑封装到一个while循环中，如下代码：

    while (oldStartIdx <= oldEndIdx && newStartIdx <= newEndIdx) {
        if (oldStartVNode.key === newStartVNode.key) {
            // 第一步比较
        } else if (oldEndVNode.key === newEndVNode.key) {
            // 第二步比较
        } else if (oldStartVNode.key === newEndVNode.key) {
            // 第三步比较
        } else if (oldEndVNode.key === newStartVNode.key) {
            // 第四步比较
            // 仍然调用patch函数进行打补丁
            patch(oldEndVNode, newStartVNode, container);
            // 移动DOM操作
            insert(oldEndVNode.el, container, oldStartVNode.el);
            // 移动DOM完成后,更新索引值,并指向下一个位置
            oldEndVNode = oldChildren[--oldEndIdx];
            newStartVNode = newChildren[++newStartIdx];
        }
    }

在第一轮更新结束后循环条件仍然成立，因此需要进行下一轮比较，如上图所示，第二轮更新：

  • 第一步：比较旧vnode中的头部节点 p-1与新vnode中的头部节点p-2，key不同不可复用。
  • 第二步：比较旧vnode中的尾部节点 p-3与新vnode中的尾部节点p-3，key相同可以复用。

此时的代码：

    while (oldStartIdx <= oldEndIdx && newStartIdx <= newEndIdx) {
        if (oldStartVNode.key === newStartVNode.key) {
            // 第一步比较
        } else if (oldEndVNode.key === newEndVNode.key) {
            patch(oldEndVNode, newEndVNode, container);
            // 节点在新的顺序中仍然处于尾部,不需要insert来移动
            oldEndVNode = oldChildren[--oldEndIdx];
            newEndVNode = newChildren[--newEndIdx];
        } else if (oldStartVNode.key === newEndVNode.key) {
            // 第三步比较
        } else if (oldEndVNode.key === newStartVNode.key) {
            patch(oldEndVNode, newStartVNode, container);
            insert(oldEndVNode.el, container, oldStartVNode.el);
            oldEndVNode = oldChildren[--oldEndIdx];
            newStartVNode = newChildren[++newStartIdx];
        }
    }

第二轮更新完成后，此时新旧vnode与真实DOM的状态：

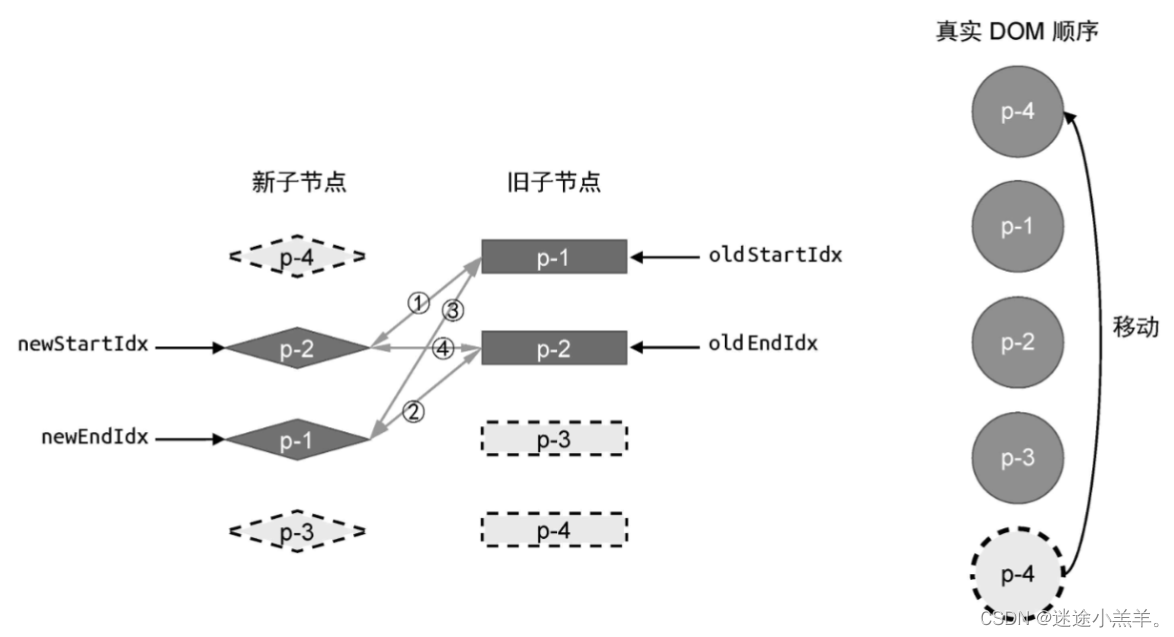
在这里插入图片描述

真实DOM的顺序相比上一轮没有变化，因为在这一轮的比较中没有对DOM节点进行移动，只是对p-3节点打补丁。

接下来继续进行下一轮的比较，具体步骤与前面类似，省略了，直接看图吧：
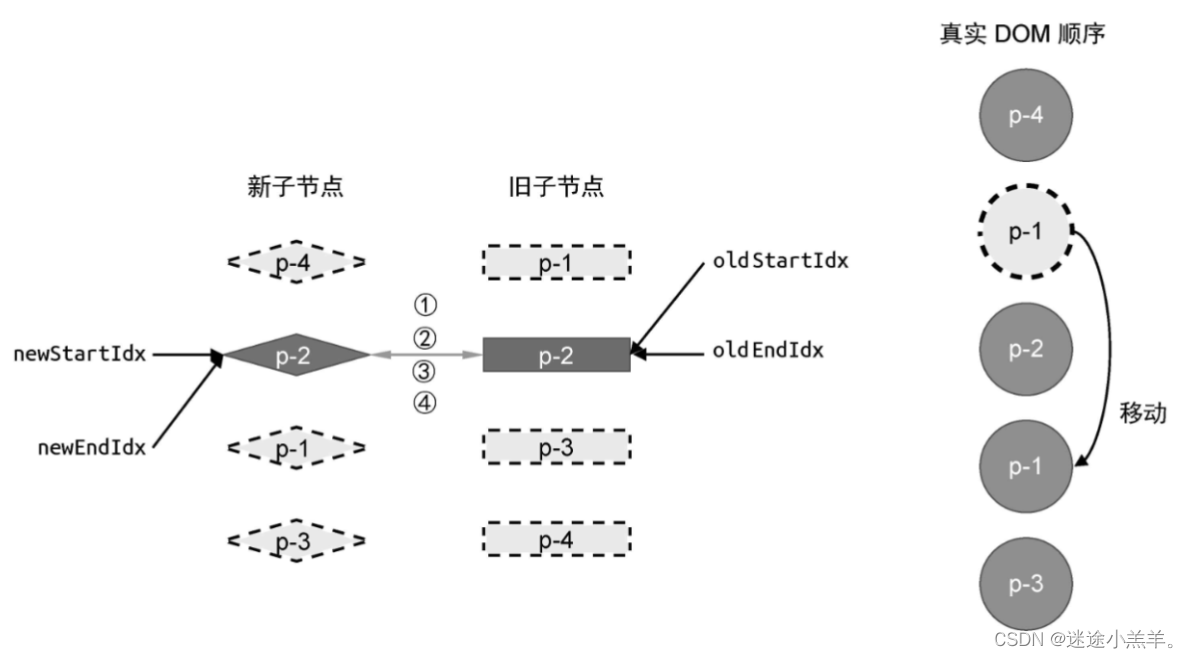
在这里插入图片描述

这是在第三步的比较中找到了相同的节点，即比较旧vnode的头部节点与新vnode的尾部节点p-1（在第二轮比较中，尾部节点自减发生了变化），两者的key相同，可以复用。

因此需要将节点p-1 对应的真实DOM移动到旧vnode的尾部节点p-2 所对应的真实DOM后面，并且更新索引，如图：
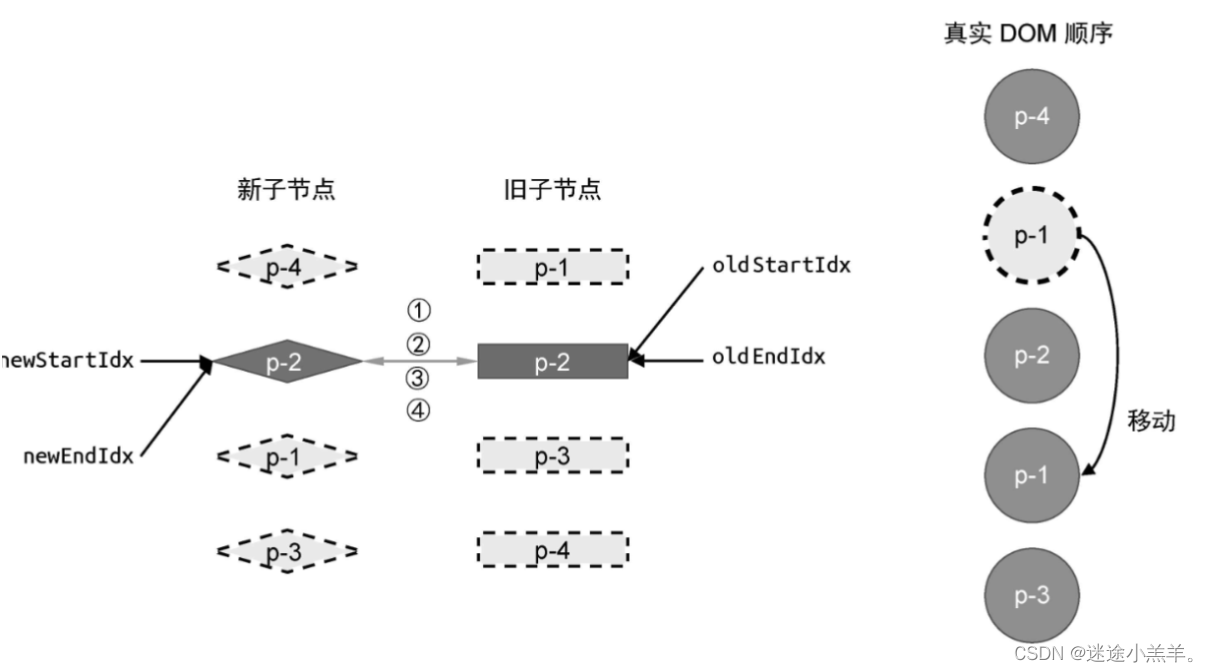
在这里插入图片描述

如下代码：

    while (oldStartIdx <= oldEndIdx && newStartIdx <= newEndIdx) {
        if (oldStartVNode.key === newStartVNode.key) {
            // 第一步比较
        } else if (oldEndVNode.key === newEndVNode.key) {
            patch(oldEndVNode, newEndVNode, container);
            // 节点在新的顺序中仍然处于尾部,不需要insert来移动
            oldEndVNode = oldChildren[--oldEndIdx];
            newEndVNode = newChildren[--newEndIdx];
        } else if (oldStartVNode.key === newEndVNode.key) {
            patch(oldStartVNode, newEndVNode, container);
            // 移动DOM到旧vnode的尾部节点对应的真实DOM节点后面
            insert(oldStartVNode.el, container, oldEndVNode.el.nextSibling);
            oldStartVNode = oldChildren[++oldStartIdx];
            newEndVNode = newChildren[--newEndIdx];
        } else if (oldEndVNode.key === newStartVNode.key) {
            patch(oldEndVNode, newStartVNode, container);
            insert(oldEndVNode.el, container, oldStartVNode.el);
            oldEndVNode = oldChildren[--oldEndIdx];
            newStartVNode = newChildren[++newStartIdx];
        }
    }

如上面代码所示，如果旧vnode的头部节点与新vnode的尾部节点匹配，则说明要将旧vnode所对应的真实DOM移动到尾部。因此需要获取当前尾部节点的下一个兄弟节点作为锚点，即 oldEndVNode.el.nextSibling。最后更新相关索引到下一个位置。

最后一步，看上图可知，新旧vnode的头/尾索引发生重合，但仍然满足循环条件，所以还会进行下一轮更新。

直接上代码了，详细解释就不说了，挺简单的，把握一点即可：主要通过新旧vnode的前后指针来判断，有四种命中情况，命中一种则不再进行判断。

    while (oldStartIdx <= oldEndIdx && newStartIdx <= newEndIdx) {
        if (oldStartVNode.key === newStartVNode.key) {
            patch(oldStartVNode, newStartVNode, container);
            oldStartVNode = oldChildren[++oldStartIdx];
            newStartVNode = newChildren[++newStartIdx];
        } else if (oldEndVNode.key === newEndVNode.key) {
            patch(oldEndVNode, newEndVNode, container);
            oldEndVNode = oldChildren[--oldEndIdx];
            newEndVNode = newChildren[--newEndIdx];
        } else if (oldStartVNode.key === newEndVNode.key) {
            patch(oldStartVNode, newEndVNode, container);
            insert(oldStartVNode.el, container, oldEndVNode.el.nextSibling);
            oldStartVNode = oldChildren[++oldStartIdx];
            newEndVNode = newChildren[--newEndIdx];
        } else if (oldEndVNode.key === newStartVNode.key) {
            patch(oldEndVNode, newStartVNode, container);
            insert(oldEndVNode.el, container, oldStartVNode.el);
            oldEndVNode = oldChildren[--oldEndIdx];
            newStartVNode = newChildren[++newStartIdx];
        }
    }

此时新旧vnode与真实DOM节点如图所示：
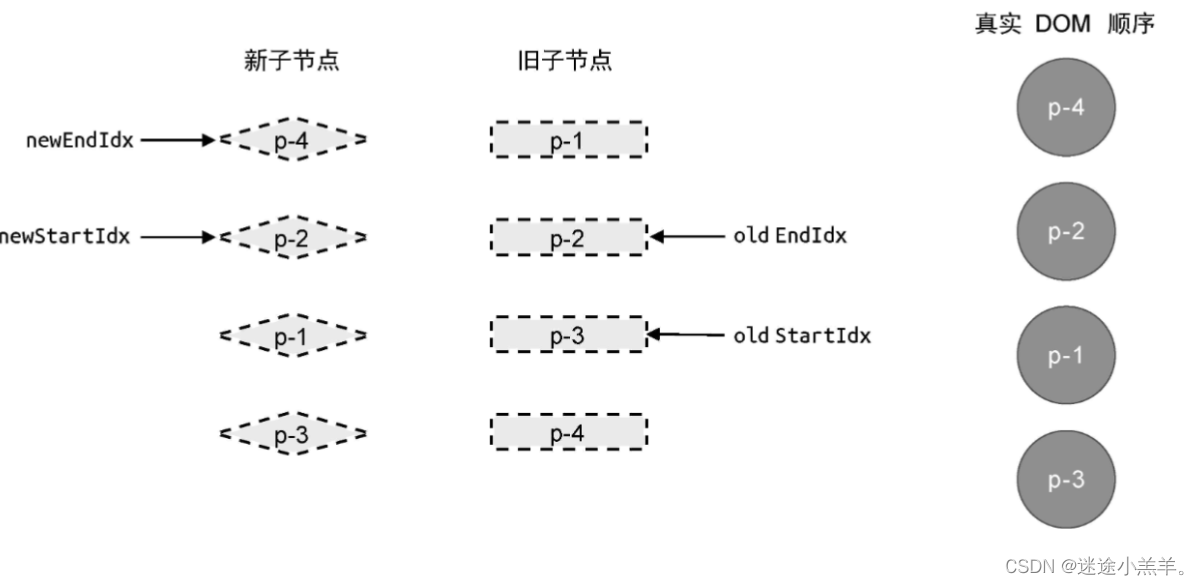
在这里插入图片描述

2.非理想状况的处理方式：

根据前面的讲解，每一轮比较都会命中四个步骤中的一个，这是比较理想的情况。那么如果没有命中呢？如下图所示：
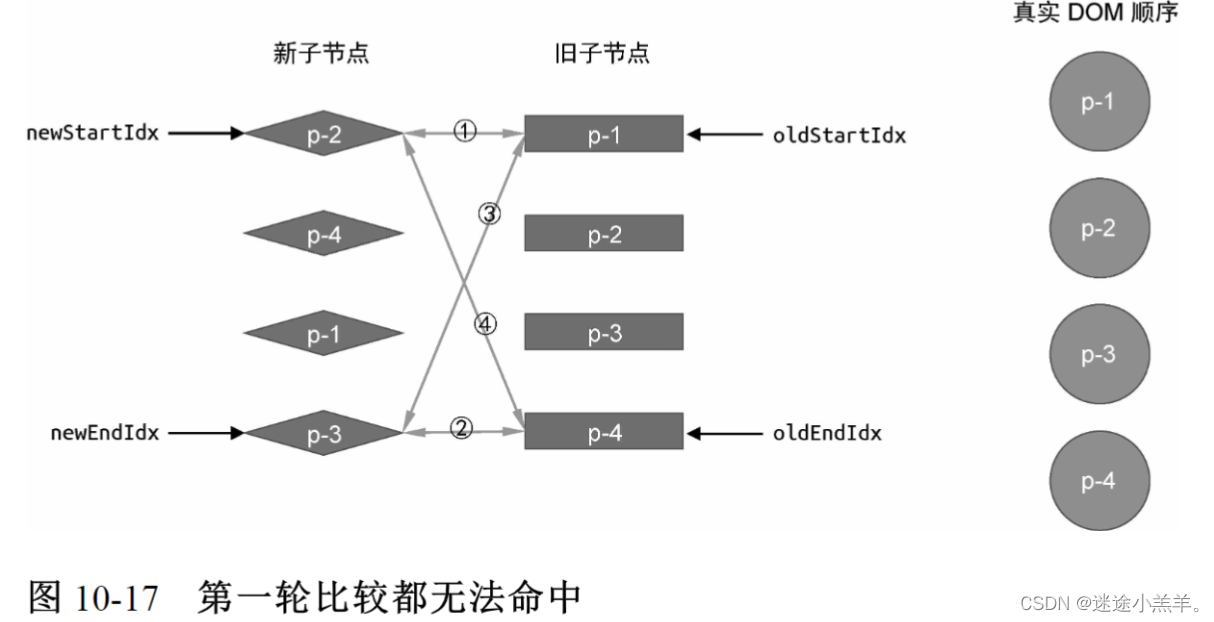
在这里插入图片描述

当尝试按照双端diff算法思路进行第一轮比较时，会发现无法命中四个步骤中的任何一步。我们只能通过额外增加的处理步骤来处理这种非理想情况。即，拿新vnode的头部节点去旧vnode的一组子节点中寻找，如下代码：

    while (oldStartIdx <= oldEndIdx && newStartIdx <= newEndIdx) {
        if (oldStartVNode.key === newStartVNode.key) {
            patch(oldStartVNode, newStartVNode, container);
            oldStartVNode = oldChildren[++oldStartIdx];
            newStartVNode = newChildren[++newStartIdx];
        } else if (oldEndVNode.key === newEndVNode.key) {
            patch(oldEndVNode, newEndVNode, container);
            oldEndVNode = oldChildren[--oldEndIdx];
            newEndVNode = newChildren[--newEndIdx];
        } else if (oldStartVNode.key === newEndVNode.key) {
            patch(oldStartVNode, newEndVNode, container);
            insert(oldStartVNode.el, container, oldEndVNode.el.nextSibling);
            oldStartVNode = oldChildren[++oldStartIdx];
            newEndVNode = newChildren[--newEndIdx];
        } else if (oldEndVNode.key === newStartVNode.key) {
            patch(oldEndVNode, newStartVNode, container);
            insert(oldEndVNode.el, container, oldStartVNode.el);
            oldEndVNode = oldChildren[--oldEndIdx];
            newStartVNode = newChildren[++newStartIdx];
        } else {
            // 遍历旧vnode,寻找与 newStartVnode有相同key的节点
            // idxInOld就是新vnode的头部节点在旧vnode中的索引
            const idxInOld = oldChildren.findIndex(
                node => node.key === newStartVNode.key
            )
        }
    }

上面增加的代码在注释里面写了，先遍历旧vnode，然后寻找与 newStartVnode 有相同key的节点，idxInOld 就是新vnode的头部节点在旧vnode中的索引。这么做的目的是啥？

先来搞清楚：在旧vnode中，找到与新vnode的头部节点具有相同key的节点意味着啥？如下图所示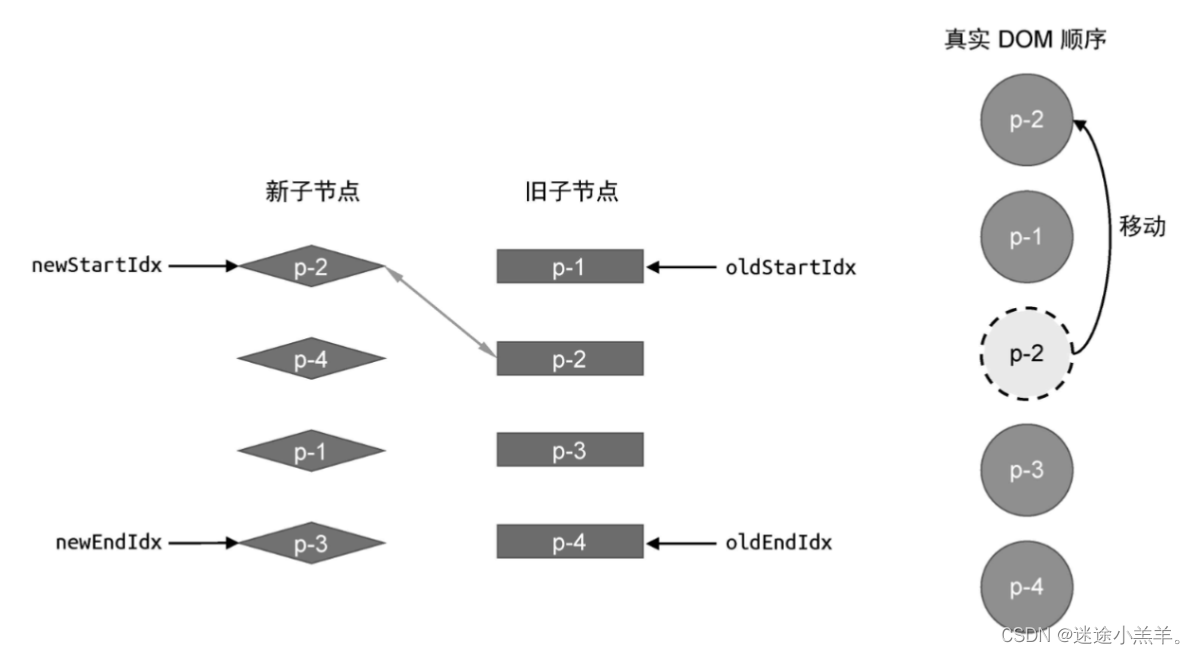：在这里插入图片描述

当我们拿新vnode的头部节点在旧vnode中寻找适，会在索引为1的位置找到可复用节点。

这意味着更新后 p-2应该变成头部节点，所以要将 p-2对应的真实DOM移动到当前旧vnode的头部节点p-1所对应的真实DOM之前。具体实现如下：

    while (oldStartIdx <= oldEndIdx && newStartIdx <= newEndIdx) {
        if (oldStartVNode.key === newStartVNode.key) {
            patch(oldStartVNode, newStartVNode, container);
            oldStartVNode = oldChildren[++oldStartIdx];
            newStartVNode = newChildren[++newStartIdx];
        } else if (oldEndVNode.key === newEndVNode.key) {
            patch(oldEndVNode, newEndVNode, container);
            oldEndVNode = oldChildren[--oldEndIdx];
            newEndVNode = newChildren[--newEndIdx];
        } else if (oldStartVNode.key === newEndVNode.key) {
            patch(oldStartVNode, newEndVNode, container);
            insert(oldStartVNode.el, container, oldEndVNode.el.nextSibling);
            oldStartVNode = oldChildren[++oldStartIdx];
            newEndVNode = newChildren[--newEndIdx];
        } else if (oldEndVNode.key === newStartVNode.key) {
            patch(oldEndVNode, newStartVNode, container);
            insert(oldEndVNode.el, container, oldStartVNode.el);
            oldEndVNode = oldChildren[--oldEndIdx];
            newStartVNode = newChildren[++newStartIdx];
        } else {
            // 遍历旧vnode,寻找与 newStartVnode有相同key的节点
            // idxInOld就是新vnode的头部节点在旧vnode中的索引
            const idxInOld = oldChildren.findIndex(
                node => node.key === newStartVNode.key
            )
            // idxInOld>0,说明找到了可复用节点,并且需要将其对应的真实DOM移动到头部
            if (idxInOld > 0) {
                // idxInOld 对应的 vnode就是需要移动的节点
                const vnodeToMove = oldChildren[idxInOld];
                // 移除操作外还应该打补丁
                patch(vnodeToMove, newStartVNode, container);
                // 将 vnodeToMove.el移动到头部节点 oldStartVnode.el之前,因此使用后者作为锚点
                insert(vnodeToMove.el, container, oldStartVNode.el);
                // 由于idxInOld处所对应的真实DOM已经移动到了别处,因此将其设置为 undefined
                oldChildren[idxInOld] = undefine;
                // 最后更新 newStartIdx到下一个位置
                newStartVNode = newChildren[++newStartIdx];
            }
        }
    }

上面代码的解释卸载了注释里了。经过上面步骤操作后，新旧vnode以及真实DOM的状态如图所示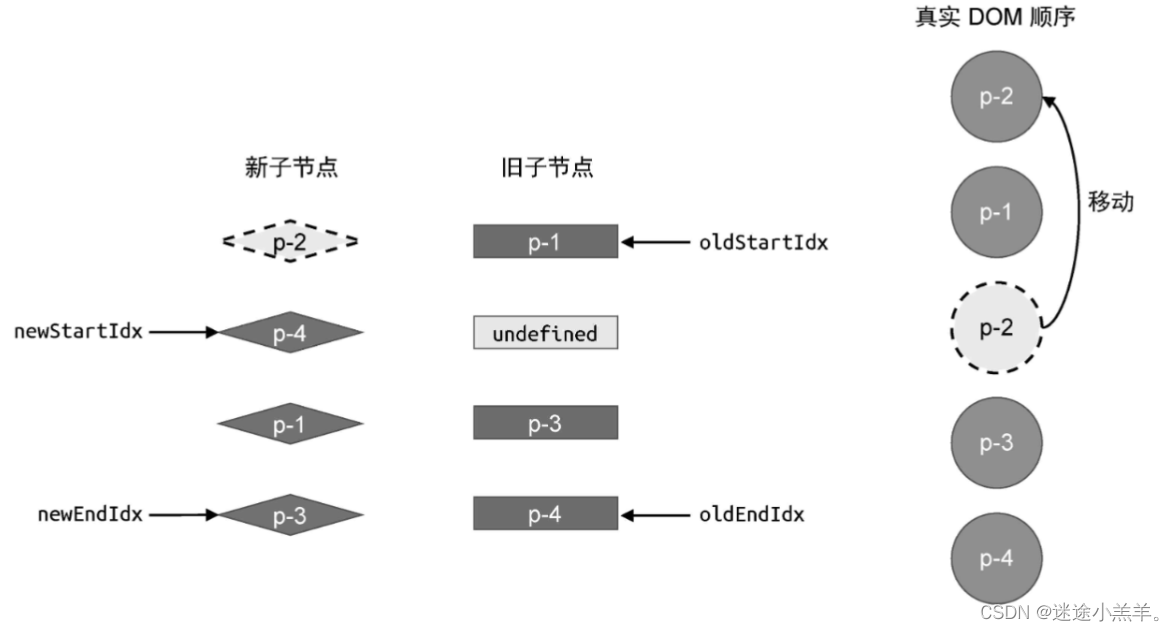：在这里插入图片描述

此时真实DOM顺序为：p-2、p-1、p-3、p-4。然后双端diff算法将继续执行（步骤跟前面一样），逻辑将变成这样：

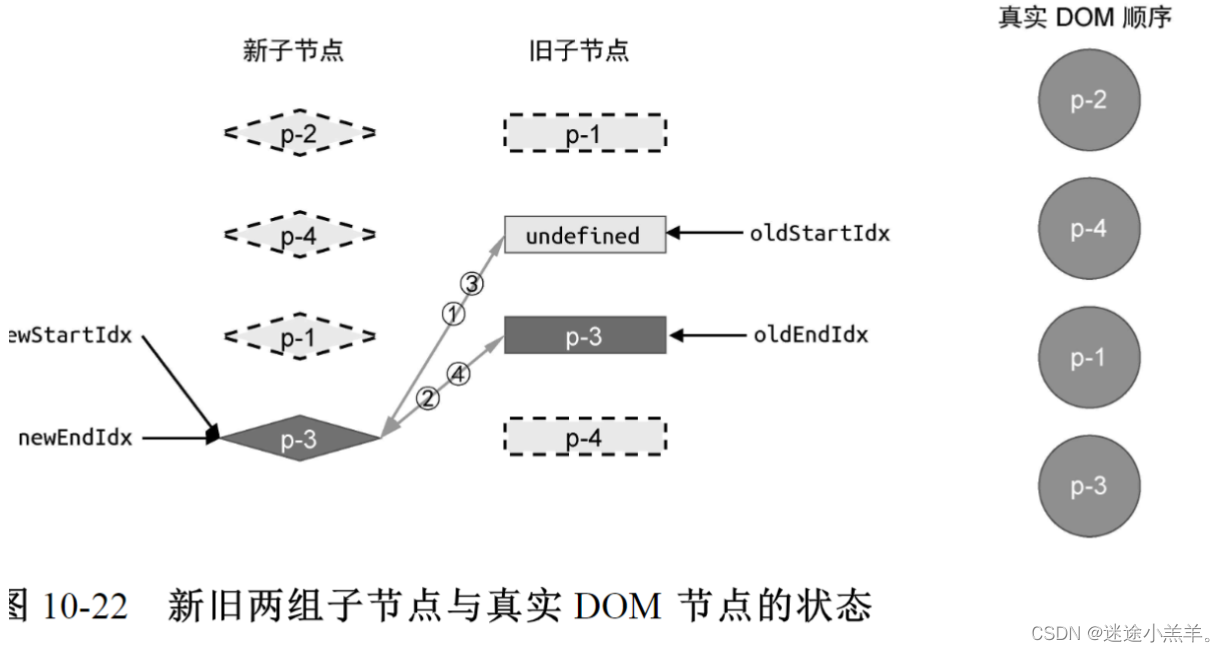
在这里插入图片描述

需要注意的是，当旧vnode的头部节点为 undefined适，说明该节点被处理过了，因此直接跳过即可。补充这部分的逻辑代码：

    while (oldStartIdx <= oldEndIdx && newStartIdx <= newEndIdx) {
        // 增加两个判断分支,如果头尾节点为undefined,则说明该节点已经被处理了,跳过
        if (!oldStartVNode) {
            oldStartVNode = oldChildren[++oldStartIdx];
        } else if (!oldEndVNode) {
            oldEndVNode = oldChildren[--oldEndIdx];
        } else if (oldStartVNode.key === newStartVNode.key) {
            patch(oldStartVNode, newStartVNode, container);
            oldStartVNode = oldChildren[++oldStartIdx];
            newStartVNode = newChildren[++newStartIdx];
        } else if (oldEndVNode.key === newEndVNode.key) {
            patch(oldEndVNode, newEndVNode, container);
            oldEndVNode = oldChildren[--oldEndIdx];
            newEndVNode = newChildren[--newEndIdx];
        } else if (oldStartVNode.key === newEndVNode.key) {
            patch(oldStartVNode, newEndVNode, container);
            insert(oldStartVNode.el, container, oldEndVNode.el.nextSibling);
            oldStartVNode = oldChildren[++oldStartIdx];
            newEndVNode = newChildren[--newEndIdx];
        } else if (oldEndVNode.key === newStartVNode.key) {
            patch(oldEndVNode, newStartVNode, container);
            insert(oldEndVNode.el, container, oldStartVNode.el);
            oldEndVNode = oldChildren[--oldEndIdx];
            newStartVNode = newChildren[++newStartIdx];
        } else {
            const idxInOld = oldChildren.findIndex(
                node => node.key === newStartVNode.key
            )
            if (idxInOld > 0) {
                const vnodeToMove = oldChildren[idxInOld];
                patch(vnodeToMove, newStartVNode, container);
                insert(vnodeToMove.el, container, oldStartVNode.el);
                oldChildren[idxInOld] = undefine;
                newStartVNode = newChildren[++newStartIdx];
            }
        }
    }

只是增加了两个判断分支，在这一轮比较过后，新旧vnode与真实DOM节点的状态如图：

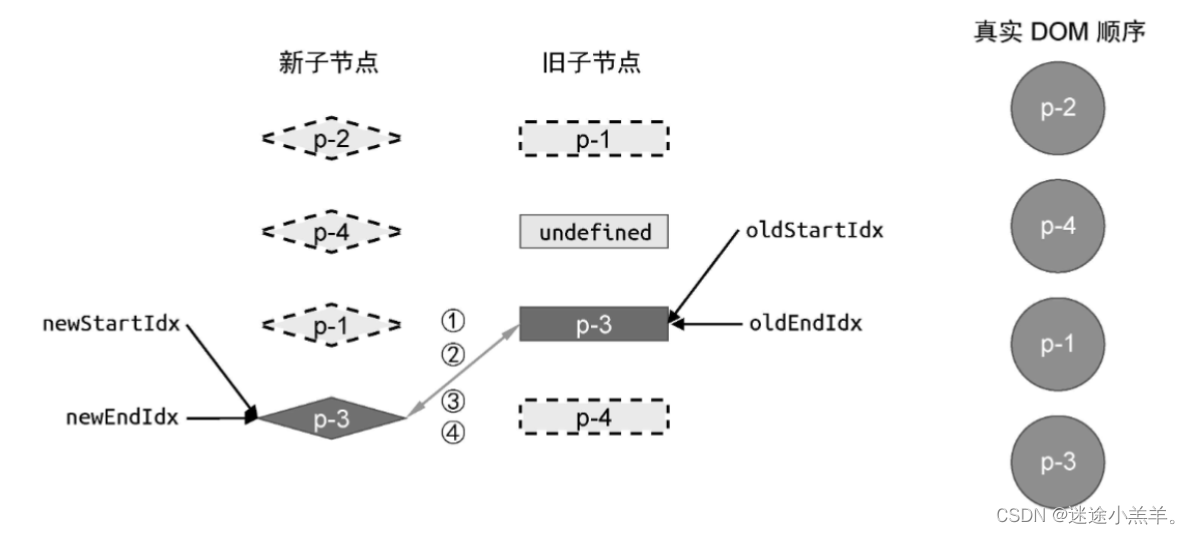
在这里插入图片描述

至此四个步骤又重合了，接着进行最后一轮的比较。

  • 第一步：比较旧vnode中的头部节点 p-3 与新vnode中的头部节点p-3，两者key值相同，进行复用。

此时不需要进行DOM移动操作，直接打补丁即可。在这一轮比较过后，最后状态如图所示：
在这里插入图片描述

这样，更新就完成了。

3.添加新元素：

在前面我们讲解了非理想情况的处理，即在一轮比较过程中，不会命中四个步骤的任何一步，这时会拿新vnode的头节点去旧vnode中寻找可复用的节点。

但是有可能存在找不到的情况，看个图就明白了：
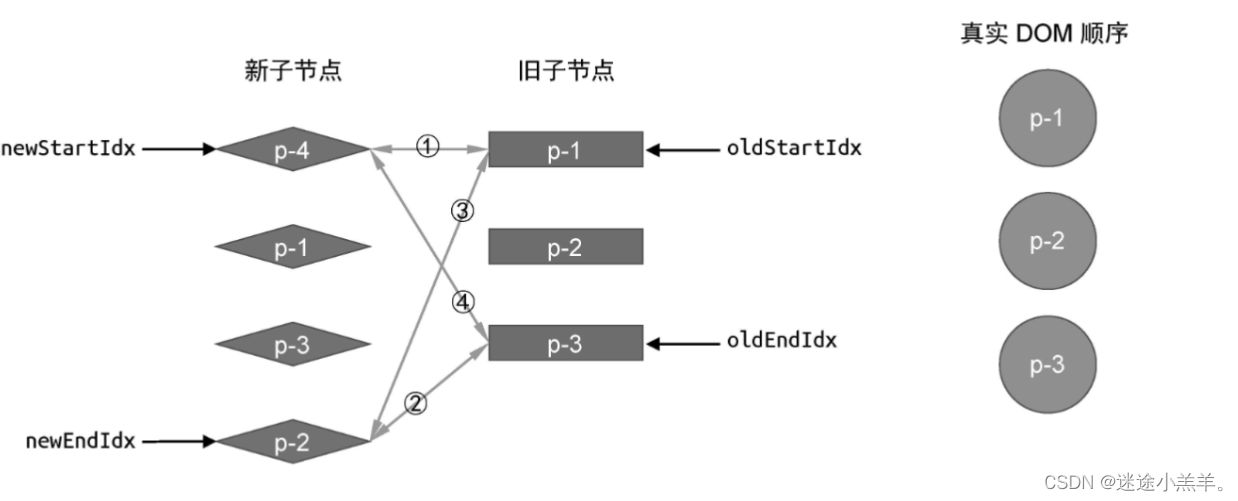
在这里插入图片描述

上图中新vnode p-4 在旧vnode中找不到可复用的节点，这说明它是一个新增节点，需要将它挂载。那么应该挂载到哪里？很简单，因为p-4是新的一组子节点中的头部节点，所以将它挂载到当前头部节点之前即可。当前头部节点：旧vnode头部节点p-1所对应的真实DOM节点。

老规矩，注释部分代表新增代码：

    while (oldStartIdx <= oldEndIdx && newStartIdx <= newEndIdx) {
        if (!oldStartVNode) {
            oldStartVNode = oldChildren[++oldStartIdx];
        } else if (!oldEndVNode) {
            oldEndVNode = oldChildren[--oldEndIdx];
        } else if (oldStartVNode.key === newStartVNode.key) {
            patch(oldStartVNode, newStartVNode, container);
            oldStartVNode = oldChildren[++oldStartIdx];
            newStartVNode = newChildren[++newStartIdx];
        } else if (oldEndVNode.key === newEndVNode.key) {
            patch(oldEndVNode, newEndVNode, container);
            oldEndVNode = oldChildren[--oldEndIdx];
            newEndVNode = newChildren[--newEndIdx];
        } else if (oldStartVNode.key === newEndVNode.key) {
            patch(oldStartVNode, newEndVNode, container);
            insert(oldStartVNode.el, container, oldEndVNode.el.nextSibling);
            oldStartVNode = oldChildren[++oldStartIdx];
            newEndVNode = newChildren[--newEndIdx];
        } else if (oldEndVNode.key === newStartVNode.key) {
            patch(oldEndVNode, newStartVNode, container);
            insert(oldEndVNode.el, container, oldStartVNode.el);
            oldEndVNode = oldChildren[--oldEndIdx];
            newStartVNode = newChildren[++newStartIdx];
        } else {
            const idxInOld = oldChildren.findIndex(
                node => node.key === newStartVNode.key
            )
            if (idxInOld > 0) {
                const vnodeToMove = oldChildren[idxInOld];
                patch(vnodeToMove, newStartVNode, container);
                insert(vnodeToMove.el, container, oldStartVNode.el);
                oldChildren[idxInOld] = undefine;
                newStartVNode = newChildren[++newStartIdx];
            } else {
                // 将 newStartVNode作为新节点挂载到头部,
                // 使用当前头部节点 oldStartVNode.el作为锚点
                patch(null, newStartVNode, container, oldStartVNode.el);
            }
            newStartVNode = newChildren[++newStartIdx];
        }
    }

如上代码所示，当条件 idxInOld > 0不成立时，说明newStartVNode节点是全新的节点，又由于这个索引表示的是新头部节点，所以需要将其进行挂载。这一步操作完成后，新旧vnode以及真实DOM节点状态如图：

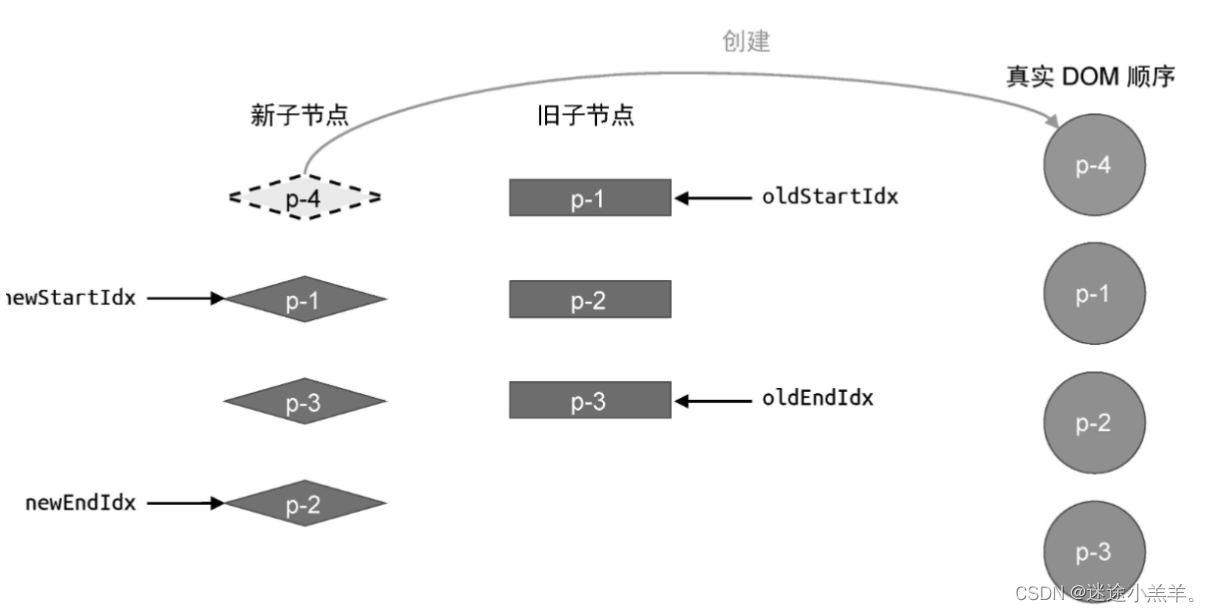
在这里插入图片描述

但是其实还是不够完美，有一个缺陷，来看一个例子：

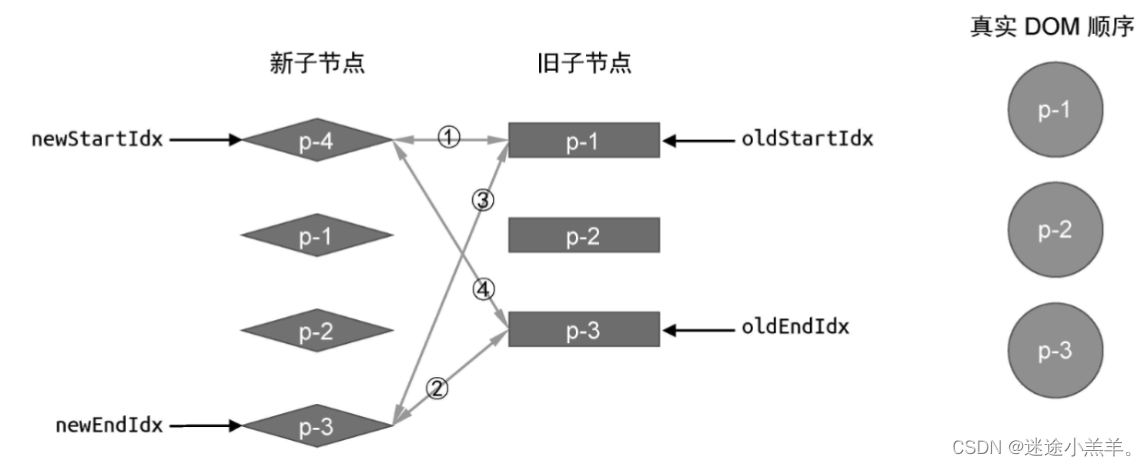
在这里插入图片描述

这个例子和前面的不同，此时新vnode的顺序是： p-4 、p-1、p-2、p-3。下面按照双端diff算法的思路来执行更新，看看会发生什么。

  • 第一轮更新：在第二步比较旧vnode的p-3 与新vnode的 p-3 中发现了可复用节点。
  • 第二轮更新：在第二步比较旧vnode的p-2 与新vnode的 p-2 中发现了可复用节点。
  • 第三轮更新…（也是在第二步）

最后更新完后的状态：（具体移动步骤啥的就省略啦，跟前面一样）
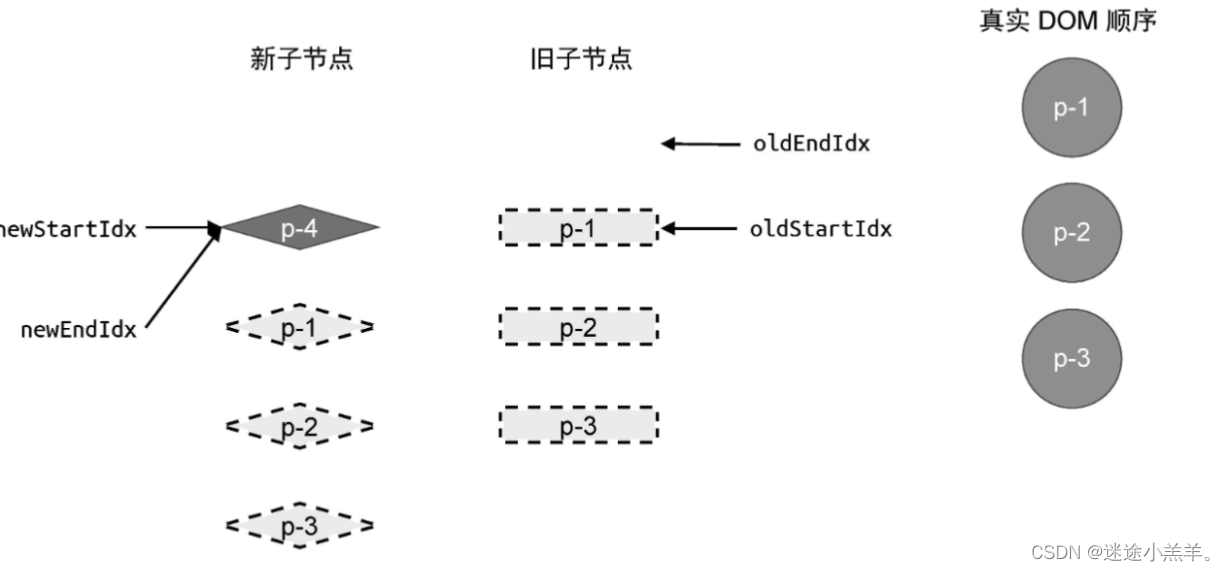
在这里插入图片描述

注意旧vnode的两个前后指针，这时满足了更新停止的 条件，但是节点p-4在整个更新过程中被遗漏了，这时就需要弥补这个缺陷，添加额外处理代码：

while (oldStartIdx <= oldEndIdx && newStartIdx <= newEndIdx) {
	// ...省略
}
// 循环结束后检查索引值的情况:
if (oldEndIdx < oldStartIdx && newStartIdx <= newEndIdx) {
	// 满足条件则说明有新节点遗留,需要进行挂载
	for (let i = newStartIdx; i <= newEndIdx; i++) {
		patch(null, newChildren[i], container, oldStartVNode.el);
        }
    }

代码解释都写在注释里了，注意一点：如何说明新vnode中有遗留的节点需要作为新vnode挂载？位于 索引值 newStartIdx 和 newEndIdx这个区间内的节点都是新节点。

4.移除不存在的元素：

解决了新增节点的问题，来思考如何移除旧vnode中多余的元素，如图：

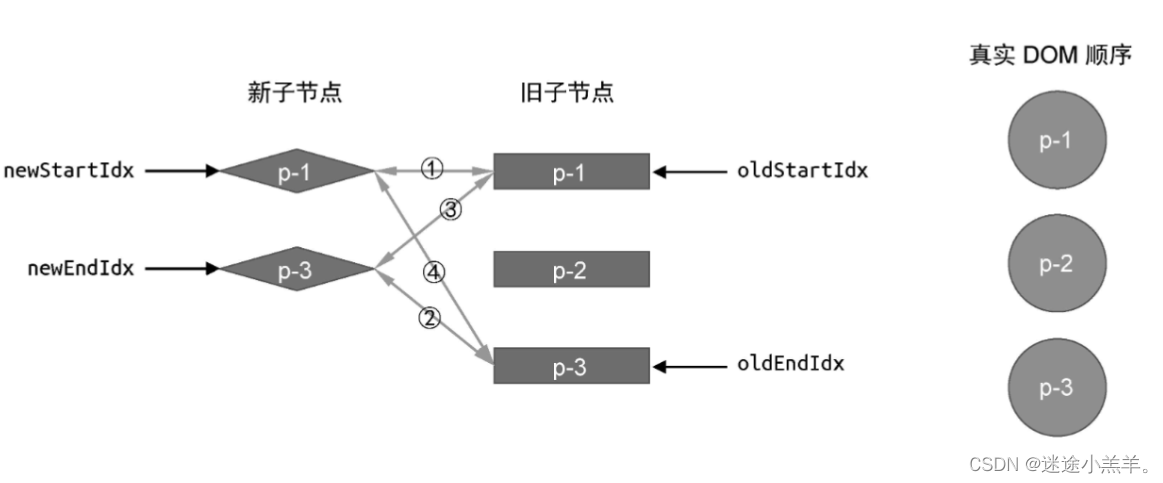
在这里插入图片描述

按照我们前面实现的diff算法来完成更新后，最后的状态应该是这样：
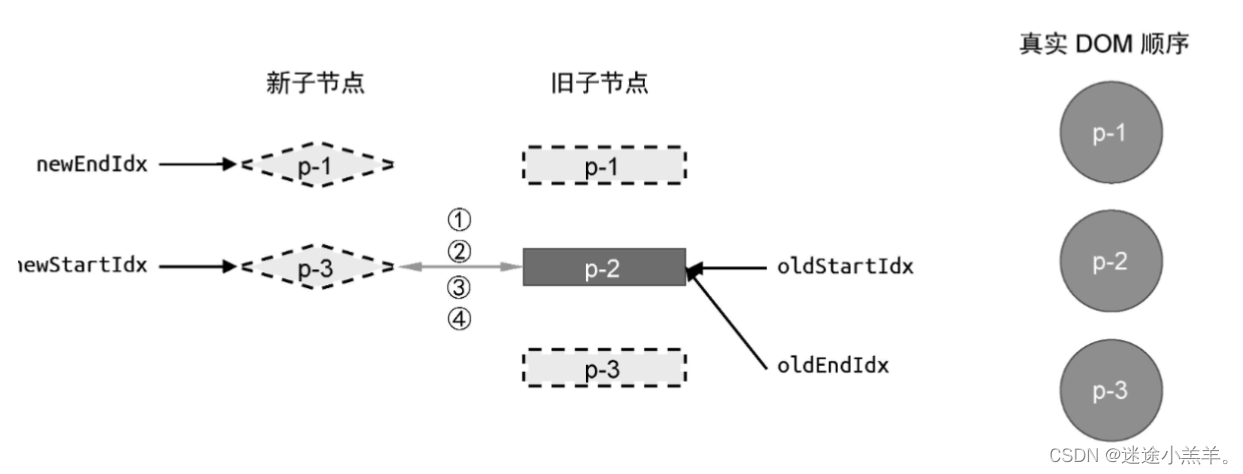
在这里插入图片描述

此时变量 newStartIdx > newEndIdx的值，满足更新停止的条件。但是看上图，旧vnode中还存在未被处理的节点，应该将其移除。所以我们需要增加额外的代码来处理它，如下图：

while (oldStartIdx <= oldEndIdx && newStartIdx <= newEndIdx) {
	// ...省略
}
// 循环结束后检查索引值的情况:
if (oldEndIdx < oldStartIdx && newStartIdx <= newEndIdx) {
	// ...省略(添加新节点)
} else if (newEndIdx < newStartIdx && oldStartIdx <= oldEndIdx) {
	// 移除操作
	for (let i = oldStartIdx; i <= oldEndIdx; i++) {
		unmount(oldChildren[i]);
	}
}

5.总结：

这章介绍了双端Diff算法的原理和优势，简单来说主要通过新旧vnode的前后指针来判断，有四种命中情况，命中一种则不再进行判断。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/88992.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

（python + 雷电模拟器）frida下载与安装

（python + 雷电模拟器）frida下载与安装

frida下载 我这边是用pycharm下载的 我是直接下载最新的&#xff0c;暂时没发现什么异常 在安装成功界面查看frida版本 此时电脑端frida下载完成。打开github&#xff0c;搜索到frida&#xff0c;点击发行版 根据你的frida版本&#xff0c;对url进行修改进入你需要的版本…
阅读更多...
方格涂色（冬季每日一题 30）

方格涂色（冬季每日一题 30）

给定一个 nnnnnn 的方格矩阵&#xff0c;最初所有方格都是白色的。 现在需要将矩阵边界上的一些方格涂成黑色&#xff0c;从而使得&#xff1a; 最上一行恰好有 UUU 个方格是黑色的。最右一列恰好有 RRR 个方格是黑色的。最下一行恰好有 DDD 个方格是黑色的。最左一列恰好有 …
阅读更多...
Android入门第47天-Fragment的基本使用

Android入门第47天-Fragment的基本使用

简介 我们的Android入门一步步已经进入中级。我们讲完了所有的基本组件的基本使用、Activity、Service、BroadCast。今天我们来到了Fragment篇章。Fragment和Activity比到底是一个什么样的存在呢&#xff1f;我们以一个很小的例子来说通Fragment。 Fragment是什么 Fragment可…
阅读更多...
智能家居DIY系列之智能灯泡

智能家居DIY系列之智能灯泡

一、什么是智能灯 传统的灯泡是通过手动打开和关闭开关来工作。有时&#xff0c;它们可以通过声控、触控、红外等方式进行控制&#xff0c;或者带有调光开关&#xff0c;让用户调暗或调亮灯光。 智能灯泡内置有芯片和通信模块&#xff0c;可与手机、家庭智能助手、或其他智能…
阅读更多...
浅析JWT Attack

浅析JWT Attack

前言 在2022祥云杯时遇到有关JWT的题&#xff0c;当时没有思路&#xff0c;对JWT进行学习后来对此进行简单总结&#xff0c;希望能对正在学习JWT的师傅们有所帮助。 JWT JWT&#xff0c;即JSON WEB TOKEN&#xff0c;它是一种用于通信双方之间传递安全信息的简洁的、URL安全…
阅读更多...
创新研发负载分担机制，天翼云IPv6网络带宽再升级！

创新研发负载分担机制，天翼云IPv6网络带宽再升级！

网络作为社会信息化的基础&#xff0c;已成为人们日常生活不可或缺的一部分。网络通过模拟信号将信息转为电流进行传播&#xff0c;在这个过程中&#xff0c;网卡便充当了解码器的作用&#xff0c;能够将电信号转换为计算机能够识别的数字信号。 网卡&#xff0c;即网络接口卡&…
阅读更多...
关于LabVIEW大作业/课设/论文的写作框架整理（主体三部曲）

关于LabVIEW大作业/课设/论文的写作框架整理（主体三部曲）

文章目录 一、前言二、写作框架2.1 介绍函数以及工具箱2.2 介绍相关原理2.3 系统设计和案例演示三、总结一、前言 因为在Labview临近要交大作业，发现自己根本不会写，程序等的已经准备好了，但是对于写作一直不知道查了查知网文章，让我有了个大概了解，在此帖出来，希望能帮…
阅读更多...
1569_AURIX_TC275_电源管理与系统控制单元

1569_AURIX_TC275_电源管理与系统控制单元

全部学习汇总&#xff1a; GreyZhang/g_TC275: happy hacking for TC275! (github.com) 之前看了不少类似的寄存器信息&#xff0c;总体来说阅读价值不是很大&#xff0c;查询的价值多一些。如果是进行编码&#xff0c;这样的寄存器信息需要查一下&#xff0c;在功能了解的时候…
阅读更多...
java面试强基（22）

java面试强基（22）

为什么要使用多线程呢? 先从总体上来说&#xff1a; 从计算机底层来说&#xff1a; 线程可以比作是轻量级的进程&#xff0c;是程序执行的最小单位,线程间的切换和调度的成本远远小于进程。另外&#xff0c;多核 CPU 时代意味着多个线程可以同时运行&#xff0c;这减少了线程…
阅读更多...
漏洞丨实例分析cve2012-0158

漏洞丨实例分析cve2012-0158

作者&#xff1a;黑蛋 作者&#xff1a;黑蛋 一、漏洞简介 CVE-2012-0158是一个office栈溢出漏洞&#xff0c;Microsoft Office 2003 sp3是2007年9月18日由微软公司创作的一个办公软件&#xff0c;他的MSCOMCTL.ocx中的MSCOMCTL.ListView控件检查失误&#xff0c;由于读取长…
阅读更多...
MySQL数据库Linux系统安装tar包

MySQL数据库Linux系统安装tar包

MySQL数据库Linux系统安装tar包 使用的远程工具是mabaxterm,使用此工具连接linux服务器&#xff0c; 第一步先把mysql安装包拖到远程工具的目录里&#xff1a;/usr/local 第二步&#xff1a;cd到local目录下解压数据库mysql 命令&#xff1a; cd …/usr/local 解压数据库masq…
阅读更多...
endo BCN-PEG4-COOH,1881221-47-1,endo BCN-四聚乙二醇-羧酸特点分享

endo BCN-PEG4-COOH,1881221-47-1,endo BCN-四聚乙二醇-羧酸特点分享

●外观以及性质&#xff1a; endo BCN-PEG4-acid含有BCN基团和羧酸基团&#xff0c;酸基团可以在偶联条件下与胺反应形成酰胺键。BCN基团可以发生点击化学反应。 【产品理化指标】&#xff1a; ●中文名&#xff1a;endo BCN-四聚乙二醇-羧酸 ●英文名&#xff1a;endo BCN-P…
阅读更多...
APS智能排产帮助LNG船舶生产厂家充分利用产能，提升生产效益

APS智能排产帮助LNG船舶生产厂家充分利用产能，提升生产效益

前一段时间&#xff0c;由于欧洲各国集中储备天然气准备过冬&#xff0c;引发全球对LNG船舶&#xff0c;也就是液化天然气运输船的需求持续增加。一艘LNG船单日租金成本已跃升至近40万美元&#xff08;约合人民币283万元&#xff09;&#xff0c;同比增长340%以上&#xff0c;一…
阅读更多...
测试面试 | 某 BAT 大厂测试开发面试真题与重点解析

测试面试 | 某 BAT 大厂测试开发面试真题与重点解析

image1080677 64.8 KB 本文作者 J2W 为霍格沃兹测试学院《测试开发实战进阶》班优秀学员&#xff0c;4 个多月从初出茅庐、勉勉强强的初级测试开发快速成长&#xff0c;成功拿下某 BAT 大厂中级测试开发岗位 Offer&#xff0c;并获得学院奖学金。助教老师对其一致评价是「学习非…
阅读更多...
程序人生：自学上岸自动化测试薪资20K，我的经验值得想进阶的朋友借鉴...

程序人生：自学上岸自动化测试薪资20K，我的经验值得想进阶的朋友借鉴...

经常有人问过这样一个问题&#xff1a;‘’自动化测试是真的这么厉害吗&#xff1f;如何从零成为自动化测试工程师&#xff1f;” 我之前写过这样一篇文章【从功能测试进阶自动化测试&#xff0c;熬夜7天整理出这一份超全学习指南【附网盘资源】】 厉害不厉害在于你有没有扎实…
阅读更多...
java-爬虫-es

java-爬虫-es

文章目录1.数据来源&#xff1a;数据库、mq、爬虫2.爬虫&#xff1a;获取想要的页面数据1.导入依赖2.爬取核心部分编码3.测试解析成功4.封装对象5.引入es配置类6.将HtmlParseUtil注册到spring7.爬取的数据入es库8.空白文件初始化vue文献&#xff1a;https://www.kuangstudy.com…
阅读更多...
Java程序员的技术进阶成长路线

Java程序员的技术进阶成长路线

据不完全统计&#xff0c;截至目前(2017.07)为止&#xff0c;中国Java程序员的数量已经超过了100万。而且&#xff0c;随着IT培训业的持续发展和大量的应届毕业生进入社会&#xff0c;Java程序员面临的竞争压力越来越大。那么&#xff0c;作为一名Java初级程序员&#xff0c;怎…
阅读更多...
【财务】FMS财务管理系统：礼品卡管理

【财务】FMS财务管理系统：礼品卡管理

本文总结了FMS财务管理系统中的礼品卡管理&#xff0c;以及如何根据不同类型卡的流程和管理&#xff0c;进行相应的账务处理。 目前在各大电子商务网站或APP购买商品时&#xff0c;在支付时有很多网站都可以使用礼品卡&#xff0c;对于礼品卡的管理也是公司及财务部重点关注的&…
阅读更多...
[附源码]Nodejs计算机毕业设计基于WEB的心理测评系统Express(程序+LW)

[附源码]Nodejs计算机毕业设计基于WEB的心理测评系统Express(程序+LW)

该项目含有源码、文档、程序、数据库、配套开发软件、软件安装教程。欢迎交流 项目运行 环境配置&#xff1a; Node.js Vscode Mysql5.7 HBuilderXNavicat11VueExpress。 项目技术&#xff1a; Express框架 Node.js Vue 等等组成&#xff0c;B/S模式 Vscode管理前后端分…
阅读更多...
Django期末考试复习

Django期末考试复习

目录一、Django复习内容二、建立一个项目1.进入环境2.建立项目3.打开文件三、建立APP1.进入View文件2.进入Django环境3.建立App四、注册超级用户1.INSTALLED_APPS配置2.建立模型3.数据库的迁移4.进入环境注册超级用户5.开启服务器五、配置数据库一、Django复习内容 二、建立一个…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023