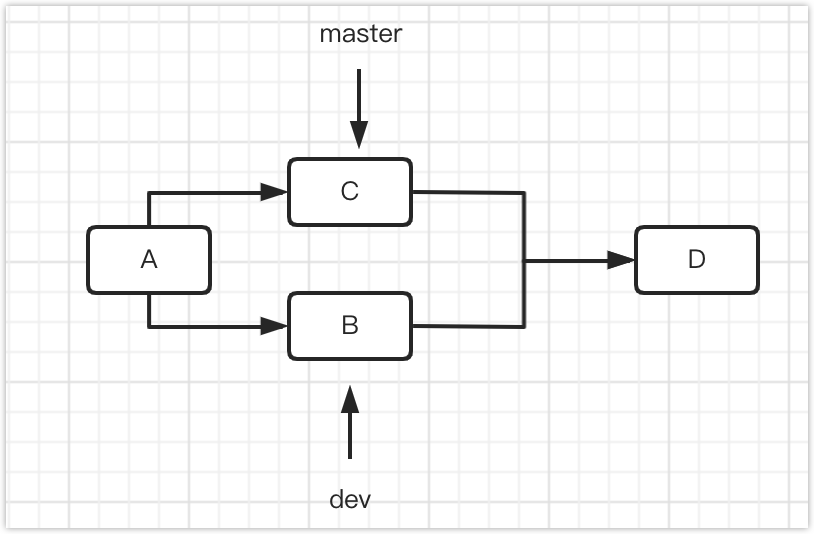
给定一个 $n\times n$ 的方格矩阵，最初所有方格都是白色的。

现在需要将矩阵边界上的一些方格涂成黑色，从而使得：

• 最上一行恰好有 $U$ 个方格是黑色的。
• 最右一列恰好有 $R$ 个方格是黑色的。
• 最下一行恰好有 $D$ 个方格是黑色的。
• 最左一列恰好有 $L$ 个方格是黑色的。

注意，你可以选择不进行任何涂色，让所有方格都保持白色。

请问，是否存在满足所有要求的合理涂色方案。

输入格式
第一行包含整数 $T$，表示共有 $T$ 组测试数据。

每组数据占一行，包含 $5$ 个整数 $n,U,R,D,L$。

输出格式
每组数据输出一行结果，如果存在合理方案，则输出 YES，否则输出 NO。

数据范围
$1\le t\le 1000,$
$2\le n\le 100,$
$0\le U,R,D,L\le n$

输入样例：

4
5 2 5 3 1
3 0 0 0 0
4 4 1 4 0
2 1 1 1 1

输出样例：

YES
YES
NO
YES

样例解释
下面是样例 $1,2,4$ 的可行方案：

---

#include<iostream>

using namespace std;

int n;
int u, r, d, l;
// 2 5 3 1
bool check(int state){
    
    int a = state >> 0 & 1, b = state >> 1 & 1;
    int x = state >> 2 & 1, y = state >> 3 & 1;
    
    if(!(u >= a + b && u <= n - 2 + a + b)) return false;
    if(!(r >= b + x && r <= n - 2 + b + x)) return false;
    if(!(d >= x + y && d <= n - 2 + x + y)) return false;
    if(!(l >= y + a && l <= n - 2 + y + a)) return false;
    
    return true;
}

int main(){
    
    int t;
    
    cin >> t;
    while(t--){
        
        cin >> n >> u >> r >> d >> l;
        
        bool flag = false;
        for(int i = 0; i < 16; i++){
            if(check(i)){
                flag = true;
                break;
            }
        }
        if(flag) puts("YES");
        else puts("NO");
    }
    
    return 0;
}