目录

数据结构之动态内存管理机制

占用块和空闲块

系统的内存管理

可利用空间表

分配存储空间的方式

空间分配与回收过程产生的问题

边界标识法管理动态内存

分配算法

回收算法

伙伴系统管理动态内存

可利用空间表中结点构成

分配算法

回收算法

总结

无用单元收集（垃圾回收机制）

总结

内存紧缩（内存碎片化处理）

分配内存空间

回收算法

总结

---

数据结构之动态内存管理机制

通过前面的学习，介绍很多具体的数据结构的存储以及遍历的方式，过程中只是很表面地介绍了数据的存储，而没有涉及到更底层的有关的存储空间的分配与回收，从本节开始将做更深入地介绍。

在使用早期的计算机上编写程序时，有关数据存储在什么位置等这样的问题都是需要程序员自己来给数据分配内存。而现在的高级语言，大大的减少了程序员的工作，不需要直接和存储空间打交道，程序在编译时由编译程序去合理地分配空间。

本章重点解决的问题是：

• 对于用户向系统提出的申请空间的请求，系统如何分配内存？
• 当用户不在使用之前申请的内存空间后，系统又如何回收？

这里的用户，不是普通意义上的用户，可能是一个普通的变量，一个应用程序，一个命令等等。只要是向系统发出内存申请的，都可以称之为用户。

占用块和空闲块

对于计算机中的内存来说，称已经分配给用户的的内存区统称为“占用块”；还未分配出去的内存区统称为“空闲块”或者“可利用空间块”。

系统的内存管理

对于初始状态下的内存来说，整个空间都是一个空闲块（在编译程序中称为“堆”）。但是随着不同的用户不断地提出存储请求，系统依次分配。

整个内存区就会分割成两个大部分：低地址区域会产生很多占用块；高地址区域还是空闲块。如图 1 所示：
 

图 1 动态分配过程中的内存状态

但是当某些用户运行结束，所占用的内存区域就变成了空闲块，如图 2 所示：
 

图 2 动态分配过程中的内存变化

此时，就形成了占用块和空闲块犬牙交错的状态。当后续用户请求分配内存时，系统有两种分配方式：
 

1. 系统继续利用高地址区域的连续空闲块分配给用户，不去理会之前分配给用户的内存区域的状态。直到分配无法进行，也就是高地址的空闲块不能满足用户的需求时，系统才会去回收之前的空闲块，重新组织继续分配；
2. 当用户运行一结束，系统马上将其所占空间进行回收。当有新的用户请求分配内存时，系统遍历所有的空闲块，从中找出一个合适的空闲块分配给用户。

合适的空闲块指的是能够满足用户要求的空闲块，具体的查找方式有多种，后续会介绍。

可利用空间表

当采用第 2 种方式时，系统需要建立一张记录所有空闲块信息的表。表的形式有两种：目录表和链表。各自的结构如图 3 所示：
 

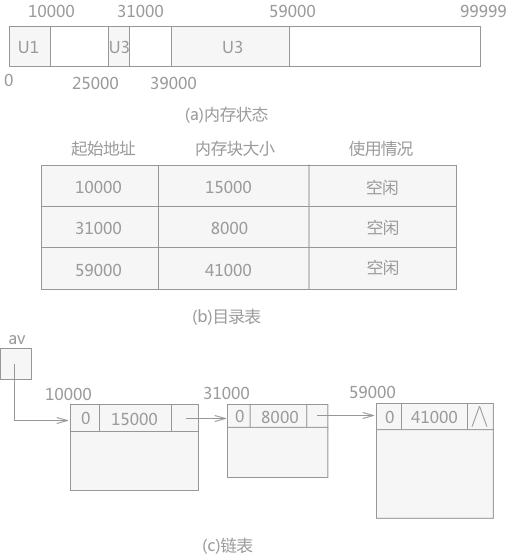
图 3 目录表和链表

目录表：表中每一行代表一个空闲块，由三部分组成：
 

• 初始地址：记录每个空闲块的起始地址。
• 空闲块大小：记录每个空闲块的内存大小。
• 使用情况：记录每个空闲块是否存储被占用的状态。

链表：表中每个结点代表一个空闲块，每个结点中需要记录空闲块的使用情况、大小和连接下一个空闲块的指针域。

由于链表中有指针的存在，所以结点中不需要记录各内存块的起始地址。

系统在不同的环境中运行，根据用户申请空间的不同，存储空闲块的可利用空间表有以下不同的结构：
 

1. 如果每次用户请求的存储空间大小相同，对于此类系统中的内存来说，在用户运行初期就将整个内存存储块按照所需大小进行分割，然后通过链表链接。当用户申请空间时，从链表中摘除一个结点归其使用；用完后再链接到可利用空间表上。
2. 每次如果用户申请的都是若干种大小规格的存储空间，针对这种情况可以建立若干个可利用空间表，每一个链表中的结点大小相同。当用户申请某一规格大小的存储空间时，就从对应的链表中摘除一个结点供其使用；用完后链接到相同规格大小的链表中。
3. 用户申请的内存的大小不固定，所以造成系统分配的内存块的大小也不确定，回收时，链接到可利用空间表中每个结点的大小也各不一样。

第 2 种情况下容易面临的问题是：如果同用户申请空间大小相同的链表中没有结点时，就需要找结点更大的链表，从中取出一个结点，一部分给用户使用，剩余部分插入到相应大小的链表中；回收时，将释放的空闲块插入到大小相同的链表中去。如果没有比用户申请的内存空间相等甚至更大的结点时，就需要系统重新组织一些小的连续空间，然后给用户使用。

分配存储空间的方式

通常情况下系统中的可利用空间表是第 3 种情况。如图 3(C) 所示。由于链表中各结点的大小不一，在用户申请内存空间时，就需要从可利用空间表中找出一个合适的结点，有三种查找的方法：
 

• 首次拟合法：在可利用空间表中从头开始依次遍历，将找到的第一个内存不小于用户申请空间的结点分配给用户，剩余空间仍留在链表中；回收时只要将释放的空闲块插入在链表的表头即可。
• 最佳拟合法：和首次拟合法不同，最佳拟合法是选择一块内存空间不小于用户申请空间，但是却最接近的一个结点分配给用户。为了实现这个方法，首先要将链表中的各个结点按照存储空间的大小进行从小到大排序，由此，在遍历的过程中只需要找到第一块大于用户申请空间的结点即可进行分配；用户运行完成后，需要将空闲块根据其自身的大小插入到链表的相应位置。
• 最差拟合法：和最佳拟合法正好相反，该方法是在不小于用户申请空间的所有结点中，筛选出存储空间最大的结点，从该结点的内存空间中提取出相应的空间给用户使用。为了实现这一方法，可以在开始前先将可利用空间表中的结点按照存储空间大小从大到小进行排序，第一个结点自然就是最大的结点。回收空间时，同样将释放的空闲块插入到相应的位置上。

以上三种方法各有所长：
 

• 最佳拟合法由于每次分配相差不大的结点给用户使用，所以会生成很多存储空间特别小的结点，以至于根本无法使用，使用过程中，链表中的结点存储大小发生两极分化，大的很大，小的很小。该方法适用于申请内存大小范围较广的系统
• 最差拟合法，由于每次都是从存储空间最大的结点中分配给用户空间，所以链表中的结点大小不会起伏太大。依次适用于申请分配内存空间较窄的系统。
• 首次拟合法每次都是随机分配。在不清楚用户申请空间大小的情况下，使用该方法分配空间。

同时，三种方法中，最佳拟合法相比于其它两种方式，无论是分配过程还是回收过程，都需要遍历链表，所有最费时间。

空间分配与回收过程产生的问题

无论使用以上三种分配方式中的哪一种，最终内存空间都会成为一个一个特别小的内存空间，对于用户申请的空间的需求，单独拿出任何一个结点都不能够满足。

但是并不是说整个内存空间就不够用户使用。在这种情况下，就需要系统在回收的过程考虑将地址相邻的空闲块合并。

边界标识法管理动态内存

在使用边界标识法的系统管理内存时，可利用空间表中的结点的构成如图 1：
 

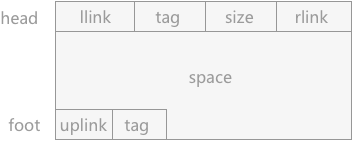
图 1 结构构成

每个结点中包含 3 个区域，head 域、foot 域 和 space 域：
 

• space 域表示为该内存块的大小，它的大小通过 head 域中的 size 值表示。
• head 域中包含有 4 部分：llink 和 rlink 分别表示指向当前内存块结点的直接前驱和直接后继。tag 值用于标记当前内存块的状态，是占用块（用 1 表示）还是空闲块（用 0 表示）。size 用于记录该内存块的存储大小。
• foot 域中包含有 2 部分：uplink 是指针域，用于指向内存块本身，通过 uplink 就可以获取该内存块所在内存的首地址。tag 同 head 域中的 tag 相同，都是记录内存块状态的。

注意：head 域和 foot 域在本节中都假设只占用当前存储块的 1 个存储单位的空间，对于该结点整个存储空间来说，可以忽略不计。也就是说，在可利用空间表中，知道下一个结点的首地址，该值减 1 就可以找到当前结点的 foot 域。

使用边界标识法的可利用空间表本身是双向循环链表，每个内存块结点都有指向前驱和后继结点的指针域。

所以，边界标识法管理的内存块结点的代码表示为：

1. typedef struct WORD{
2. union{
3. struct WORD *llink;//指向直接前驱
4. struct WORD *uplink;//指向结点本身
5. };
6. int tag;//标记域,0表示为空闲块；1表示为占用块
7. int size;//记录内存块的存储大小
8. struct WORD *rlink;//指向直接后继
9. OtherType other;//内存块可能包含的其它的部分
10. }WORD,head,foot,*Space;

通过以上介绍的结点结构构建的可利用空间表中，任何一个结点都可以作为该链表的头结点（用 pav 表示头结点），当头结点为 NULL 时，即可利用空间表为空，无法继续分配空间。

分配算法

当用户申请空间时，系统可以采用 3 种分配方法中的任何一种。但在不断地分配的过程中，会产生一些容量极小以至无法利用的空闲块，这些不断生成的小内存块就会减慢遍历分配的速度。

3 种分配方法分别为：首部拟合法、最佳拟合法和最差拟合法。

针对这种情况，解决的措施是：

1. 选定一个常量 e，每次分配空间时，判断当前内存块向用户分配空间后，如果剩余部分的容量比 e 小，则将整个内存块全部分配给用户。
2. 采用头部拟合法进行分配时，如果每次都从 pav 指向的结点开始遍历，在若干次后，会出现存储量小的结点密集地分布在 pav 结点附近的情况，严重影响遍历的时间。解决办法就是：在每次分配空间后，让 pav 指针指向该分配空间结点的后继结点，然后从新的 pav 指向的结点开始下一次的分配。

分配算法的具体实现代码为（采用首部拟合法）

1. Space AllocBoundTag(Space *pav,int n){
2. Space p,f;
3. int e=10;//设定常亮 e 的值
4. //如果在遍历过程，当前空闲块的在存储容量比用户申请空间 n 值小，在该空闲块有右孩子的情况下直接跳过
5. for (p=(*pav); p&&p->size<n&&p->rlink!=(*pav); p=p->rlink);
6. //跳出循环，首先排除p为空和p指向的空闲块容量小于 n 的情况
7. if (!p ||p->size<n) {
8. return NULL;
9. }else{
10. //指针f指向p空闲块的foot域
11. f=FootLoc(p);
12. //调整pav指针的位置，为下次分配做准备
13. (*pav)=p->rlink;
14. //如果该空闲块的存储大小比 n 大，比 n+e 小，负责第一种情况，将 p 指向的空闲块全部分配给用户
15. if (p->size-n <= e) {
16. if ((*pav)==p) {
17. pav=NULL;
18. }
19. else{
20. //全部分配用户，即从可利用空间表中删除 p 空闲块
21. (*pav)->llink=p->llink;
22. p->llink->rlink=(*pav);
23. }
24. //同时调整head域和foot域中的tag值
25. p->tag=f->tag=1;
26. }
27. //否则，从p空闲块中拿出 大小为 n 的连续空间分配给用户，同时更新p剩余存储块中的信息。
28. else{
29. //更改分配块foot域的信息
30. f->tag=1;
31. p->size-=n;
32. //f指针指向剩余空闲块 p 的底部
33. f=FootLoc(p);
34. f->tag=0; f->uplink=p;
35. p=f+1;//p指向的是分配给用户的块的head域，也就是该块的首地址
36. p->tag=1; p->size=n;
37. }
38. return p;
39. }
40. }

回收算法

在用户活动完成，系统需要立即回收被用户占用的存储空间，以备新的用户使用。回收算法中需要解决的问题是：在若干次分配操作后，可利用空间块中会产生很多存储空间很小以致无法使用的空闲块。但是经过回收用户释放的空间后，可利用空间表中可能含有地址相邻的空闲块，回收算法需要将这些地址相邻的空闲块合并为大的空闲块供新的用户使用。

合并空闲块有 3 种情况：

• 该空闲块的左边有相邻的空闲块可以进行合并；
• 该空闲块的右边用相邻的空闲块可以进行合并；
• 该空闲块的左右两侧都有相邻的空闲块可以进行合并；

判断当前空闲块左右两侧是否为空闲块的方法是：对于当前空闲块 p ，p-1 就是相邻的低地址处的空闲块的 foot 域，如果 foot 域中的 tag 值为 0 ，表明其为空闲块； p+p->size 表示的是高地址处的块的 head 域，如果 head 域中的 tag 值为 0，表明其为空闲块。

如果当前空闲块的左右两侧都不是空闲块，而是占用块，此种情况下只需要将新的空闲块按照相应的规则（头部拟合法随意插入，其它两种方法在对应位置插入）插入到可利用空间表中即可。实现代码为：

1. //设定p指针指向的为用户释放的空闲块
2. p->tag=0;
3. //f指针指向p空闲块的foot域
4. Space f=FootLoc(p);
5. f->uplink=p;
6. f->tag=0;
7. //如果pav指针不存在，证明可利用空间表为空，此时设置p为头指针，并重新建立双向循环链表
8. if (!pav) {
9. pav=p->llink=p->rlink=p;
10. }else{
11. //否则，在p空闲块插入到pav指向的空闲块的左侧
12. Space q=pav->llink;
13. p->rlink=pav;
14. p->llink=q;
15. q->rlink=pav->llink=p;
16. pav=p;
17. }

如果该空闲块的左侧相邻的块为空闲块，右侧为占用块，处理的方法是：只需要更改左侧空闲块中的 size 的大小，并重新设置左侧空闲块的 foot 域即可（如图 2）。

 

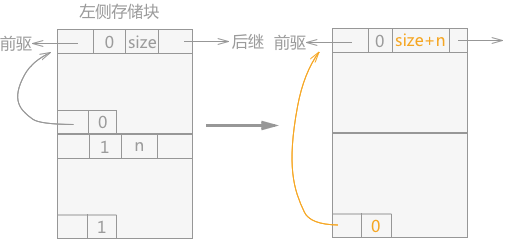
图 2 空闲块合并（当前块，左侧内存块）

实现代码为：

1. //常量 n 表示当前空闲块的存储大小
2. int n=p->size;
3. Space s=(p-1)->uplink;//p-1 为当前块的左侧块的foot域，foot域中的uplink指向的就是左侧块的首地址，s指针代表的是当前块的左侧存储块
4. s->size+=n;//设置左侧存储块的存储容量
5. Space f=p+n-1;//f指针指向的是空闲块 p 的foot域
6. f->uplink=s;//这是foot域的uplink指针重新指向合并后的存储空间的首地址
7. f->tag=0;//设置foot域的tag标记为空闲块

如果用户释放的内存块的相邻左侧为占用块，右侧为空闲块，处理的方法为：将用户释放掉的存储块替换掉右侧的空闲块，同时更改存储块的 size 和右侧空闲块的 uplink 指针的指向（如图 3 所示）。

 

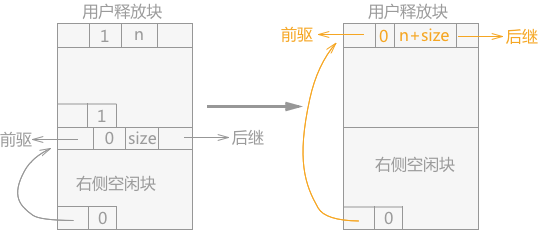
图 3 空闲块合并（当前块、右侧内存块）

实现代码为：

1. Space t=p+p->size;//t指针指向右侧空闲块的首地址
2. p->tag=0;//初始化head域的tag值为0
3. //找到t右侧空闲块的前驱结点和后继结点，用当前释放的空闲块替换右侧空闲块
4. Space q=t->llink;
5. p->llink=q; q->rlink=p;
6. Space q1=t->rlink;
7. p->rlink=q1; q1->llink=p;
8. //更新释放块的size的值
9. p->size+=t->size;
10. //更改合并后的foot域的uplink指针的指向
11. Space f=FootLoc(t);
12. f->uplink=p;

如果当前用户释放掉的空闲块，物理位置上相邻的左右两侧的内存块全部为空闲块，需要将 3 个空闲块合并为一个更大的块，操作的过程为：更新左侧空闲块的 size 的值，同时在可利用空间表中摘除右侧空闲块，最后更新合并后的大的空闲块的 foot 域。

此情况和只有左侧有空闲块的情况雷同，唯一的不同点是多了一步摘除右侧相邻空闲块结点的操作。

实现代码为：

纯文本复制

1. int n=p->size;
2. Space s=(p-1)->uplink;//找到释放内存块物理位置相邻的低地址的空闲块
3. Space t=p+p->size;//找到物理位置相邻的高地址处的空闲块
4. s->size+=n+t->size;//更新左侧空闲块的size的值
5. //从可利用空间表中摘除右侧空闲块
6. Space q=t->llink;
7. Space q1=t->rlink;
8. q->rlink=q1;
9. q1->llink=q;
10. //更新合并后的空闲块的uplink指针的指向
11. Space f=FootLoc(t);
12. f->uplink=s;

伙伴系统管理动态内存

伙伴系统本身是一种动态管理内存的方法，和边界标识法的区别是：使用伙伴系统管理的存储空间，无论是空闲块还是占用块，大小都是 2 的 n 次幂（n 为正整数）。

例如，系统中整个存储空间为 2m 个字。那么在进行若干次分配与回收后，可利用空间表中只可能包含空间大小为：20、21、22、…、2m 的空闲块。

字是一种计量单位，由若干个字节构成，不同位数的机器，字所包含的字节数不同。例如，8 位机中一个字由 1 个字节组成；16 位机器一个字由 2 个字节组成。

可利用空间表中结点构成

伙伴系统中可利用空间表中的结点构成如图 1 所示：
 

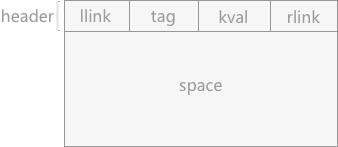
图 1 结点构成

header 域表示为头部结点，由 4 部分构成：

• llink 和 rlink 为结点类型的指针域，分别用于指向直接前驱和直接后继结点。
• tag 值：用于标记内存块的状态，是占用块（用 1 表示）还是空闲块（用 0 表示）
• kval ：记录该存储块的容量。由于系统中各存储块都是 2 的 m 幂次方，所以 kval 记录 m 的值。

代码表示为：

1. typedef struct WORD_b{
2. struct WORD_b *llink;//指向直接前驱
3. int tag;//记录该块是占用块还是空闲块
4. int kval;//记录该存储块容量大小为2的多少次幂
5. struct WORD_b *rlink;//指向直接后继
6. OtherType other;//记录结点的其它信息
7. }WORD_b,head;

在伙伴系统中，由于系统会不断地接受用户的内存申请的请求，所以会产生很多大小不同但是都是容量为 2m 的内存块，所以为了在分配的时候查找方便，系统采用将大小相同的各自建立一个链表。对于初始容量为 2m 的一整块存储空间来说，形成的链表就有可能有 m+1 个，为了更好的对这些链表进行管理，系统将这 m+1 个链表的表头存储在数组中，就类似于邻接表的结构，如图 2。

 

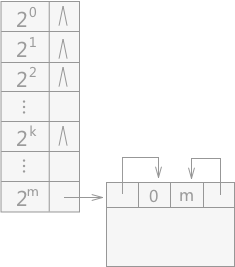
图 2 伙伴系统的初始状态

可利用空间表的代码表示为：

1. #define m 16//设定m的初始值
2. typedef struct HeadNode {
3. int nodesize;//记录该链表中存储的空闲块的大小
4. WORD_b * first;//相当于链表中的next指针的作用
5. }FreeList[m+1];//一维数组

分配算法

伙伴系统的分配算法很简单。假设用户向系统申请大小为 n 的存储空间，若 2k-1 < n <= 2k，此时就需要查看可利用空间表中大小为 2k 的链表中有没有可利用的空间结点：

• 如果该链表不为 NULL，可以直接采用头插法从头部取出一个结点，提供给用户使用；
• 如果大小为 2k 的链表为 NULL，就需要依次查看比 2k 大的链表，找到后从链表中删除，截取相应大小的空间给用户使用，剩余的空间，根据大小插入到相应的链表中。

例如，用户向系统申请一块大小为 7 个字的空间，而系统总的内存为 24 个字，则此时按照伙伴系统的分配算法得出：22 < 7 < 23，所以此时应查看可利用空间表中大小为 23 的链表中是否有空闲结点：

• 如果有，则从该链表中摘除一个结点，直接分配给用户使用；
• 如果没有，则需依次查看比 23 大的各个链表中是否有空闲结点。假设，在大小 24 的链表中有空闲块，则摘除该空闲块，分配给用户 23 个字的空间，剩余 23 个字，该剩余的空闲块添加到大小为 23 的链表中。

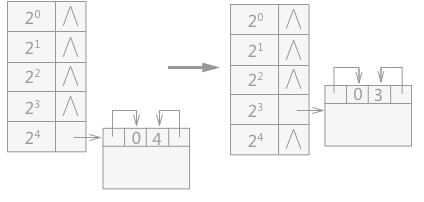
（A）分配前                       （B）分配后
图 3 伙伴系统分配过程

回收算法

无论使用什么内存管理机制，在内存回收的问题上都会面临一个共同的问题：如何把回收的内存进行有效地整合，伙伴系统也不例外。

当用户申请的内存块不再使用时，系统需要将这部分存储块回收，回收时需要判断是否可以和其它的空闲块进行合并。

在寻找合并对象时，伙伴系统和边界标识法不同，在伙伴系统中每一个存储块都有各自的“伙伴”，当用户释放存储块时只需要判断该内存块的伙伴是否为空闲块，如果是则将其合并，然后合并的新的空闲块还需要同其伙伴进行判断整合。反之直接将存储块根据大小插入到可利用空间表中即可。

判断一个存储块的伙伴的位置时，采用的方法为：如果该存储块的起始地址为 p，大小为 2k，则其伙伴所在的起始地址为：

 

 

例如，当大小为 28 ，起始地址为 512 的伙伴块的起始地址的计算方式为：
由于 512 MOD 29=0，所以，512+28=768，及如果该存储块回收时，只需要查看起始地址为 768 的存储块的状态，如果是空闲块则两者合并，反之直接将回收的释放块链接到大小为 28 的链表中。

总结

使用伙伴系统进行存储空间的管理过程中，在用户申请空间时，由于大小不同的空闲块处于不同的链表中，所以分配完成的速度会更快，算法相对简单。

回收存储空间时，对于空闲块的合并，不是取决于该空闲块的相邻位置的块的状态；而是完全取决于其伙伴块。

所以即使其相邻位置的存储块时空闲块，但是由于两者不是伙伴的关系，所以也不会合并。这也就是该系统的缺点之一：由于在合并时只考虑伙伴，所以容易产生存储的碎片。

无用单元收集（垃圾回收机制）

通过前几节对可利用空间表进行动态存储管理的介绍，运行机制可以概括为：

1. 当用户发出申请空间的请求后，系统向用户分配内存；
2. 用户运行结束释放存储空间后，系统回收内存。

这两部操作都是在用户给出明确的指令后，系统对存储空间进行有效地分配和回收。

但是在实际使用过程中，有时会因为用户申请了空间，但是在使用完成后没有向系统发出释放的指令，导致存储空间既没有被使用也没有被回收，变为了无用单元或者会产生悬挂访问的问题。

什么是无用单元？简单来讲，无用单元是一块用户不再使用，但是系统无法回收的存储空间。例如在C语言中，用户可以通过 malloc 和 free 两个功能函数来动态申请和释放存储空间。当用户使用 malloc 申请的空间使用完成后，没有使用 free 函数进行释放，那么该空间就会成为无用单元。

悬挂访问也很好理解：假设使用 malloc 申请了一块存储空间，有多个指针同时指向这块空间，当其中一个指针完成使命后，私自将该存储空间使用 free 释放掉，导致其他指针处于悬空状态，如果释放掉的空间被再分配后，再通过之前的指针访问，就会造成错误。数据结构中称这种访问为悬挂访问。
 

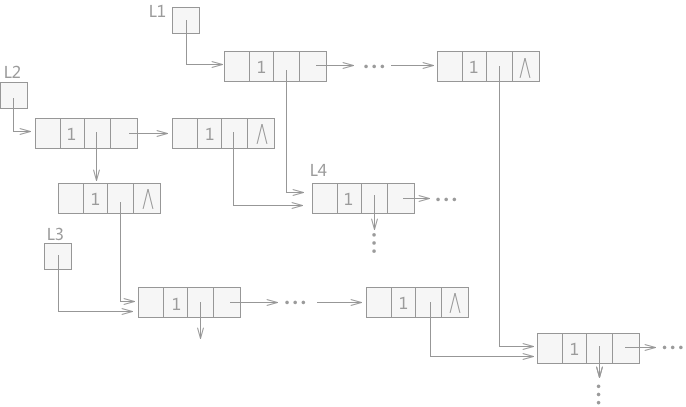
图 1 含有共享子表的广义表

在含有共享子表的广义表中，也可能会产生无用单元。例如图 1 中，L1、L2 和 L3 分别为三个广义表的表头指针，L4 为 L1 和 L2 所共享，L3 是 L2 的子表，L5 为 L1、L2 和 L3 三个广义表所共享。

在图 1 的基础上，假设表 L1 不再使用，而 L2 和 L3 还在使用，若释放表 L1，L1 中的所有结点所占的存储空间都会被释放掉，L2 和 L3 中由于同样包含 L1 中的结点，两个表会被破坏，某些指针会产生悬挂访问的错误；

而如果 L1 表使用完成后不及时释放，L1 中独自占用的结点由于未被释放，系统也不会回收，就会成为无用单元。

解决存储空间可能成为无用单元或者产生悬挂访问的方法有两个：

1. 每个申请的存储空间设置一个计数域，这个计数域记录的是指向该存储空间的指针数目，只有当计数域的值为 0 时，该存储空间才会被释放。
2. 在程序运行时，所有的存储空间无论是处于使用还是空闲的状态，一律不回收，当系统中的可利用空间表为空时，将程序中断，对当前不在使用状态的存储空间一律回收，全部链接成一个新的可利用空间表后，程序继续执行。

第一种方法非常简单，下面主要介绍第二种方法的具体实现。

第二种方法中，在程序运行过程中很难找出此时哪些存储空间是空闲的。解决这个问题的办法是：找当前正在被占用的存储空间，只需要从当前正在工作的指针变量出发依次遍历，就可以找到当前正在被占用的存储空间，剩余的自然就是此时处于空闲状态的存储空间。

如果想使用第二种方式，可以分为两步进行：

• 对所有当前正在使用的存储空间加上被占用的标记（对于广义表来说，可以在每个结点结构的基础上，添加一个 mark 的标志域。在初始状态下，所有的存储空间全部标志为 0，被占用时标记为 1）；
• 依次遍历所有的存储空间，将所有标记为 0 的存储空间链接成一个新的可利用空间表。

对正在被占用的存储空间进行标记的方法有三种：

• 从当前正在工作的指针变量开始，采用递归算法依次将所有表中的存储结点中的标志域全部设置为 1；
• 第一种方法中使用递归算法实现的遍历。而递归底层使用的栈的存储结构，所以也可以直接使用栈的方式进行遍历；
• 以上两种方法都是使用栈结构来记录遍历时指针所走的路径，便于在后期可以沿原路返回。所以第三种方式就是使用其他的方法代替栈的作用。

递归和非递归方式在前面章节做过详细介绍，第三种实现方式中代替栈的方法是：添加三个指针，p 指针指向当前遍历的结点，t 指针永远指向 p 的父结点，q 指向 p 结点的表头或者表尾结点。在遍历过程遵循以下原则：

当 q 指针指向 p 的表头结点时，可能出现 3 种情况：

• p 结点的表头结点只是一个元素结点，没有表头或者表尾，这时只需要对该表头结点打上标记后即 q 指向 p 的表尾；
• p 结点的表头结点是空表或者是已经做过标记的子表，这时直接令 q 指针指向 p 结点的表尾即可；
• p 结点的表头是未添加标记的子表，这时就需要遍历子表，令 p 指向 q，q 指向 q 的表头结点。同时 t 指针相应地往下移动，但是在移动之前需要记录 t 指针的移动轨迹。记录的方法就是令 p 结点的 hp 域指向 t，同时设置 tag 值为 0。

当 q 指针指向 p 的表尾结点时，可能出现 2 种情况：

• p 指针的表尾是未加标记的子表，就需要遍历该子表，和之前的类似，令 p 指针和 t 指针做相应的移动，在移动之前记录 t 指针的移动路径，方法是：用 p 结点的 tp 域指向 t 结点，然后在 t 指向 p，p 指向 q。
• p 指针的表尾如果是空表或者已经做过标记的结点，这时 p 结点和 t 结点都回退到上一个位置。

由于 t 结点的回退路径分别记录在结点的 hp 域或者 tp 域中，在回退时需要根据 tag 的值来判断：如果 tag 值为 0 ，t 结点通过指向自身 hp 域的结点进行回退；反之，t 结点通过指向其 tp 域的结点进行回退。

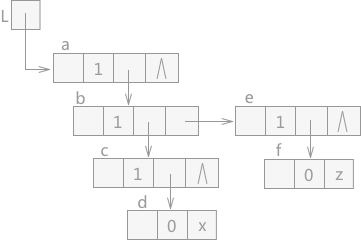
图 2 待遍历的广义表

例如，图 2 中为一个待遍历的广义表，其中每个结点的结构如图 3 所示：
 

图 3 广义表中各结点的结构

在遍历如图 2 中的广义表时，从广义表的 a 结点开始，则 p 指针指向结点 a，同时 a 结点中 mark 域设置为 1，表示已经遍历过，t 指针为 nil，q 指针指向 a 结点的表头结点，初始状态如图 4 所示：
 

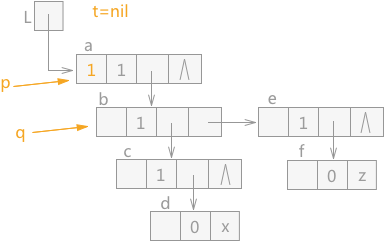
图 4 遍历广义表的初始状态

由于 q 指针指向的结点 b 的 tag 值为 1，表示该结点为表结构，所以此时 p 指向 q，q 指向结点 c，同时 t 指针下移，在 t 指针指向结点 a 之前，a 结点中的 hp 域指向 t，同时 a 结点中 tag 值设为 0。效果如图 5 所示：
 

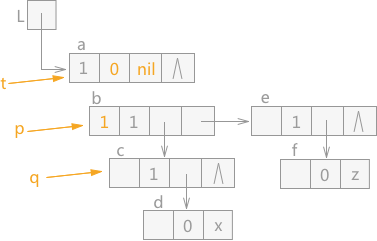
图 5 遍历广义表（2）
 

通过 q 指针指向的结点 c 的 tag=1，判断该结点为表结点，同样 p 指针指向 c，q 指针指向 d，同时 t 指针继续下移，在 t 指针指向 结点 b 之前，b 结点的 tag 值更改为 0，同时 hp 域指向结点 a，效果图如图 6 所示：
 

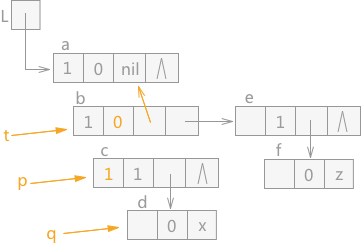
图 6 遍历广义表（3）

通过 q 指针指向的结点 d 的 tag=0，所以，该结点为原子结点，此时根据遵循的原则，只需要将 q 指针指向的结点 d 的 mark 域标记为 1，然后让 q 指针直接指向 p 指针指向结点的表尾结点，效果图如图 7 所示：
 

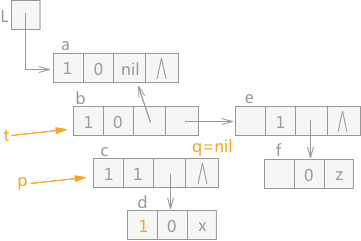
图 7 遍历广义表（4）
 

当 q 指针指向 p 指针的表尾结点时，同时 q 指针为空，这种情况的下一步操作为 p 指针和 t 指针全部上移动，即 p 指针指向结点 b，同时 t 指针根据 b 结点的 hp 域回退到结点 a。同时由于结点 b 的tag 值为 0，证明之前遍历的是表头，所以还需要遍历 b 结点的表尾结点，同时将结点 b 的 tag 值改为 1。效果图如图 8 所示：
 

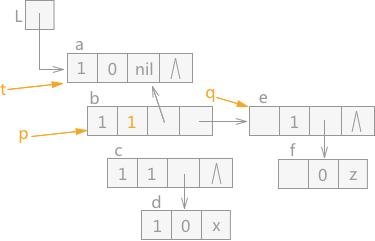
图 8 遍历广义表（5）
 

由于 q 指针指向的 e 结点为表结点，根据 q 指针指向的 e 结点是 p 指针指向的 b 结点的表尾结点，所以所做的操作为：p 指针和 t 指针在下移之前，令 p 指针指向的结点 b 的 tp 域指向结点 a，然后给 t 赋值 p，p 赋值 q。q 指向 q 的表头结点 f。效果如图 9 所示：
 

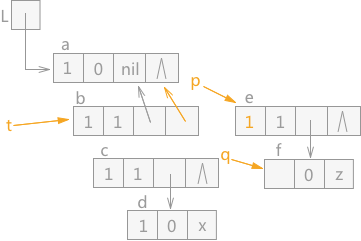
图 9 遍历广义表（6）

由于 q 指针指向的结点 f 为原子结点，所以直接 q 指针的 mark 域设为 1 后，直接令 q 指针指向 p 指针指向的 e 结点的表尾结点。效果如图 10 所示：
 

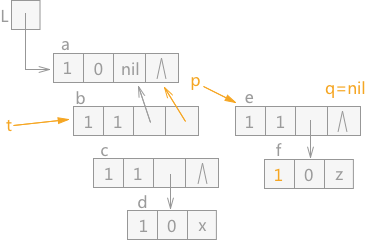
图 10 遍历广义表（7）
 

由于 p 指针指向的 e 结点的表尾结点为空，所以 p 指针和 t 指针都回退。由于 p 指针指向的结点 b 的 tag 值为 1，表明表尾已经遍历完成，所以 t 指针和 p 指针继续上移，最终遍历完成。

总结

无用单元的收集可以采用以上 3 中算法中任何一种。无论使用哪种算法，无用单元收集本身都是很费时间的，所以无用单元的收集不适用于实时处理的情况中使用。

内存紧缩（内存碎片化处理）

前边介绍的有关动态内存管理的方法，无论是边界标识法还是伙伴系统，但是以将空闲的存储空间链接成一个链表，即可利用空间表，对存储空间进行分配和回收。

本节介绍另外一种动态内存管理的方法，使用这种方式在整个内存管理过程中，不管哪个时间段，所有未被占用的空间都是地址连续的存储区。

这些地址连续的未被占用的存储区在编译程序中称为堆。

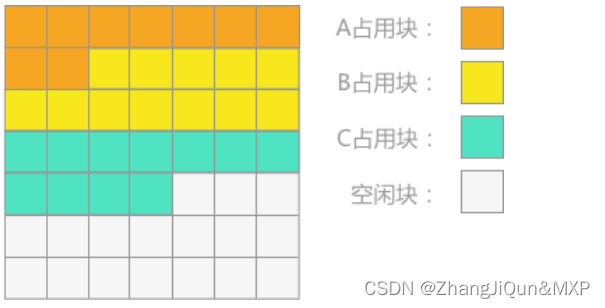
图 1 存储区状态

假设存储区的初始状态如图 1 所示，若采用本节介绍的方法管理这块存储区，当 B 占用块运行完成同时所占的存储空间释放后，存储区的状态应如图 2 所示：

 

图 2 更新后的存储区状态

分配内存空间

在分配内存空间时，每次都从可利用空间中选择最低（或者最高）的地址进行分配。具体的实现办法为：设置一个指针（称为堆指针），每次用户申请存储空间时，都是堆的最低（或者最高）地址进行分配。假设当用户申请 N 个单位的存储空间时，堆指针向高地址（或者低地址）移动 N 个存储单位，这 N 个存储单位即为分配给用户使用的空闲块，空闲块的起始地址为堆指针移动之前所在的地址。

例如，某一时间段有四个用户（A、B、C、D）分别申请 12 个单位、6 个单位、10 个单位和 8 个单位的存储空间，假设此时堆指针的初值为 0。则分配后存储空间的效果为：

回收算法

由于系统中的可利用空间始终都是一个连续的存储空间，所以回收时必须将用户释放的存储块合并到这个堆上才能够重新使用。

存储紧缩有两种做法：

1. 其一是一旦用户释放所占空间就立即进行回收紧缩；
2. 另外一种是在程序执行过程中不立即回收用户释放的存储块，而是等到可利用空间不够分配或者堆指针指向了可利用存储区的最高地址时才进行存储紧缩。

具体的实现过程是：

1. 计算占用块的新地址。设立两个指针随巡查向前移动，分别用于指示占用块在紧缩之前和之后的原地址和新地址。因此，在每个占用块的第一个存储单位中，除了存储该占用块的大小和标志域之外，还需要新增一个新地址域，用于存储占用块在紧缩后应有的新地址，即建立一张新、旧地址的对照表。
2. 修改用户的出事变量表，保证在进行存储紧缩后，用户还能找到自己的占用块。
3. 检查每个占用块中存储的数据。如果有指向其它存储块的指针，则需作相应修改。
4. 将所有占用块迁移到新地址去，即进行数据的传递。

最后，还要将堆指针赋以新的值。

总结

存储紧缩较之无用单元收集更为复杂，是一个系统的操作，如果不是非不得已不建议使用。