对于主成分分析详细的介绍:主成分分析(PCA)原理详解![]() https://blog.csdn.net/zhongkelee/article/details/44064401
https://blog.csdn.net/zhongkelee/article/details/44064401
import numpy as np
import pandas as pd
'''标准PCA算法'''
def standeredPCA(data,N): #data:数据集DataFrame N:降维后需要的维数
n=data.shape[1] #数据集data的列数,即维度
m=data.shape[0] #数据集data的行数
colname=list(data.columns) #提取列名
AVG=[] #原始各个维度的平均值
for i in range(n):
avg=0
s=list(data[colname[i]])
num=len(s)
for j in s:
avg+=j
avg=avg/num
AVG.append(avg)
'''将每一列数据都转换成列表型'''
df=[] #存储每一列的数据
for i in range(n):
ls=list(data[colname[i]])
df.append(ls)
'''数据中心化'''
for i in range(n):
t=df[i]
for j in range(len(t)):
t[j]=t[j]-AVG[i]
'''求特征协方差矩阵'''
A=np.zeros((n,n))
for i in range(n):
for j in range(n):
p=df[i]
q=df[j]
for k in range(m):
A[i][j]+=p[k]*q[k]
A[i][j]=A[i][j]/(m-1)
'''求协方差的特征值和特征向量'''
B=np.linalg.eig(A)
P=B.eigenvalues #特征值
Q=B.eigenvectors #特征向量
U=[index for index, value in sorted(list(enumerate(P)), key=lambda x:x[1])] #对特征值排序输出索引值序列
U=sorted(U,reverse=True) #特征值从大到小排序的索引值
u=[] #输出排在前N个的索引值
for i in range(N):
u.append(U[i])
r=[] #需要的特征值
t=[] #需要的特征向量
for i in u:
r.append(P[i])
T=[]
for j in Q:
T.append(j[i])
t.append(T)
'''得到通过PCA后获得的N个特征的数据'''
W=[] #存储通过PCA后得到的每一个特征的数据【列表】
for i in range(N):
a=[] #存储通过PCA的特征数据
b=t[i]
for j in range(m): #遍历数据的行
f=0
for k in range(n): #遍历数据的列
f=f+df[k][j]*b[k]
a.append(f)
W.append(a)
'''输出经过PCA降维处理后得到的N个特征数据'''
fdata=pd.DataFrame(W)
fdata=fdata.T
print("经过PCA降维后得到的结果如下:")
print(fdata)
'''计算特征信息提取率'''
sum=0
for i in P:
sum+=i
fsum=0
for i in u:
fsum+=P[i]
PCAprecent=fsum/sum
print("PCA数据特征的信息提取率是:{}".format(PCAprecent))
if __name__=="__main__":
df = {'x': [2.5, 0.5, 2.2, 1.9, 3.1, 2.3, 2, 1, 1.5, 1.1], 'y': [2.4, 0.7, 2.9, 2.2, 3.0, 2.7, 1.6, 1.1, 1.6, 0.9]}
data = pd.DataFrame(df)
standeredPCA(data, 1) 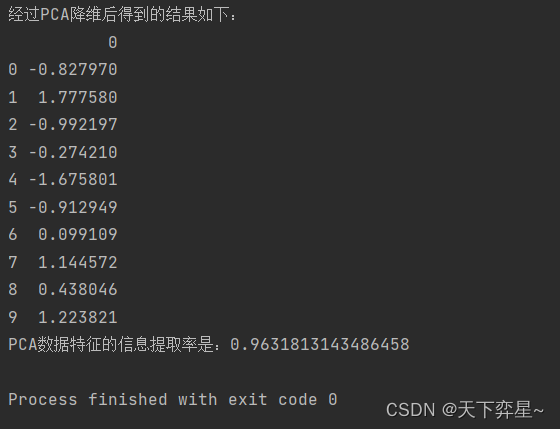



![[C++]笔记-函数的栈空间(避免栈空间溢出)](https://img-blog.csdnimg.cn/cdb2ef309d7f4cd3a6e4d99918bcb5f5.png)