看到这么大的数据规模就直到用暴力法肯定会超时,但是还是花一分钟写了一个试一下,果然超时
class Solution {
public int countDigitOne(int n) {
int count =0;
for(int i=1;i<=n;i++){
count+=digitOneInOneNum(i);
}
return count;
}
public int digitOneInOneNum(int n){
int count =0;
while(n != 0){
if(n % 10 ==1)count++;
n /=10;
}
return count;
}
}
然后自己想了好多种方法,试了很多次都有没考虑到的地方,真的挺想自己做出来的,因为这道hrad题感觉没有那么难,但是写了一个多小时也没做出来,只好看题解了,题解的方法自己想到了一点点,就是去统计每一位上1出现的次数然后加起来,但是没把情况分明白。以下是题解代码:
class Solution {
public int countDigitOne(int n) {
// mulk 表示 10^k
// 在下面的代码中,可以发现 k 并没有被直接使用到(都是使用 10^k)
// 但为了让代码看起来更加直观,这里保留了 k
int ans = 0;
long mulk = 1;
for(int i =0;n>=mulk;i++){
mulk = (int)Math.pow(10,i);
ans += (n/(mulk*10))*mulk + Math.min(Math.max(n % (mulk*10)-mulk+1, 0), mulk);
mulk*=10;
}
return ans;
}
}我们统计每一位上1出现的次数,然后全部加起来就是0-n中1出现的次数,先以百位为例,然后扩展到任意位上。
以 n=1234567 为例,我们需要统计「百位」上数字 1出现的次数。我们知道,对于从 0 开始每 1000个数,「百位」上的数字 1都会出现 100次,即数的最后三位每 1000个数都呈现 [000,999]的循环,其中的 [100,199]在「百位」上的数字为 1,共有 100个。n有1234个这样的循环,所以百位上的1就出现了1234*100次,所以百位上1出现的次数就是[n/1000]*100,[]表示向下取整。
我们刚才考虑的是前面的1234会让后面出现1234次0-999的循环,导致百位出现了[1234/1000]*100个1,现在我们还要考虑后面的567让百位出现了几次1。首先拿1234567%1000就得到了后面的567,记n' = n%1000, 那么n‘在百位上1出现的次数可以分类讨论得出:
1.n' < 100: 百位上1出现的次数为0;
2.100<=n'<200: 百位上1出现的次数是n'-100+1;
3.n'>=200; 百位上1出现的次数是100;
综合这三种情况可以发现,n'导致百位上1出现的次数为:min(max(n′−100+1,0),100)
总的1出现的次数就是前面的1234导致的1出现加上后面的567导致的1出现的次数之和,也就是
⌊1000n⌋×100+min(max(nmod1000−100+1,0),100)
那么我们再把这个公式推广到任意位上,10的k次方位上(k=0,1,2时,表示个位,十位,百位)1出现的次数为:
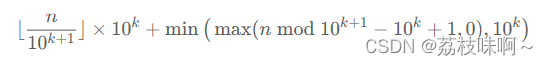
所以子只要遍历每一个k(0,1,2……直到n的最高位)然后把每一位上1出现的次数加起来就可以了。







![[C++]笔记-函数的栈空间(避免栈空间溢出)](https://img-blog.csdnimg.cn/cdb2ef309d7f4cd3a6e4d99918bcb5f5.png)