忙了一阵子，回来继续更新

3.3 代价函数公式

In order to implement linear regression. The first key step is first to define something called a cost function. This is something we’ll build in this video, and the cost function will tell us how well the model is doing so that we can try to get it to do better. Let’s look at what this means.
为了实现线性回归，第一个关键步骤是先定义一个叫作代价函数的东西。在此视频中，我们将构建这个代价函数，代价函数将告诉我们模型的表现如何，以便我们可以尝试使模型变得更好。让我们看看代价函数是什么意思。

Recall that you have a training set that contains input features x and output targets y. The model you’re going to use to fit this training set is this linear function f_w, b of x equals to w times x plus b. To introduce a little bit more terminology the w and b are called the parameters of the model.
回想一下，你有一个包含输入特征 x 和输出目标 y 的训练集。你要使用的模型是用来将这个训练集的数据拟合为一个线性函数 $f_{w,b}(x)=wx+b$。为了描述的更专业一些，我们将$w$和 $b$ 称为模型的参数。

In machine learning parameters of the model are the variables you can adjust during training in order to improve the model. Sometimes you also hear the parameters w and b referred to as coefficients or as weights. Now let’s take a look at what these parameters w and b do.
在机器学习中，模型的参数是可以在训练过程中进行调整以改善模型性能的变量。有时你也会听到参数 $w$ 和 $b$ 被称为系数或权重。现在让我们来看看这些参数 $w$ 和 $b$ 的作用。

Depending on the values you’ve chosen for w and b you get a different function f of x, which generates a different line on the graph. Remember that we can write f of x as a shorthand for f_w, b of x. We’re going to take a look at some plots of f of x on a chart.
根据所选择的 $w$ 和 $b$ 的值，你会得到一个不同的函数 $f(x)$，这将在图表上生成一条不同的线。记住，我们可以用 $f(x)$来简写 $f_{w,b}(x)$。接下来，我们将看一些 $f(x)$ 在图表上的绘图。

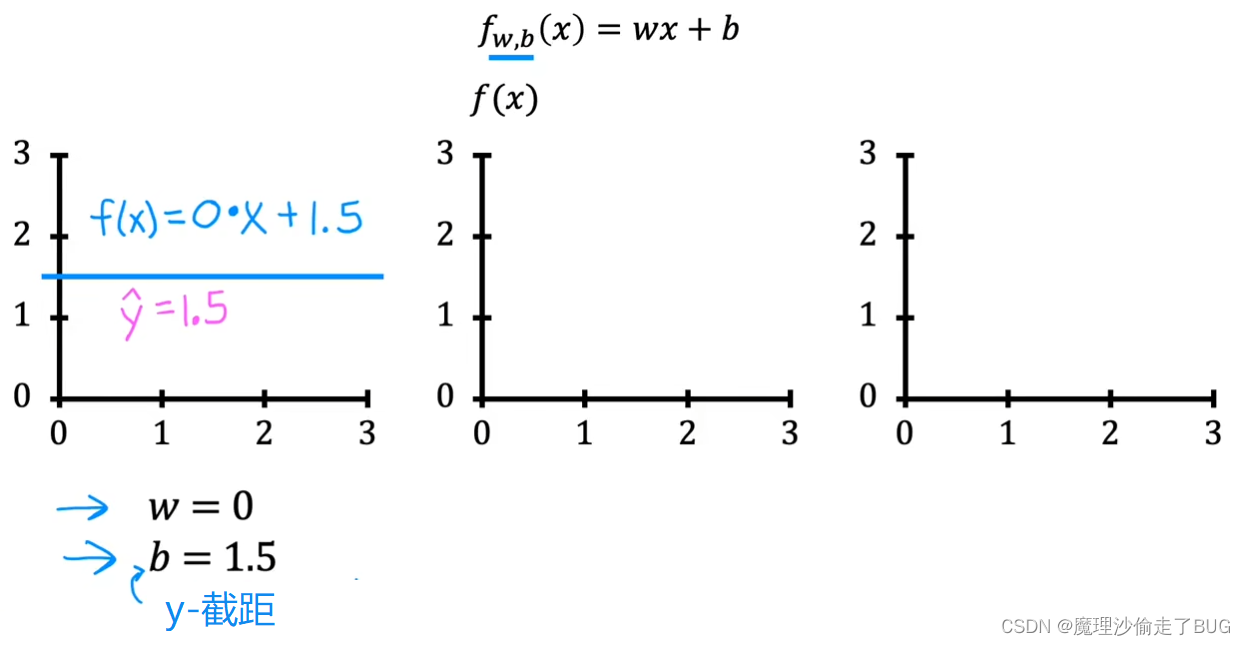
Maybe you’re already familiar with drawing lines on charts, but even if this is a review for you, I hope this will help you build intuition on how w and b the parameters determine f. When w is equal to 0 and b is equal to 1.5, then f looks like this horizontal line. In this case, the function f of x is 0 times x plus 1.5 so f is always a constant value. It always predicts 1.5 for the estimated value of y. Y hat is always equal to b and here b is also called the y intercept because that’s where it crosses the vertical axis or the y axis on this graph.
也许你已经熟悉在图表上绘制线条，但即使这对你来说是复习，我希望这能帮助你建立如何用参数 $w$ 和 $b$ 确定函数 $f$的直觉。当 $w=0$，$b=1.5$时，函数 $f$ 就像是一条水平线。在这种情况下，函数 $f(x)=0\times x+1.5$ ，因此 $f$ 始终是一个常数值。它总是对估计的 $y$ 值预测为 1.5。 $\hat{y}=b$，而在这里$b$也被称为$y$截距（y intercept），因为它是函数在图表上穿过垂直轴或y轴的位置。

As a second example, if w is 0.5 and b is equal 0, then f of x is 0.5 times x. When x is 0, the prediction is also 0, and when x is 2, then the prediction is 0.5 times 2, which is 1. You get a line that looks like this and notice that the slope is 0.5 divided by 1. The value of w gives you the slope of the line, which is 0.5.
作为第二个示例，如果$w=0.5$，$b=0$，那么$f(x)=0.5x$. 当$x=0$时，预测值也为0，当$x=2$时，预测值就是$0.5\times 2=1$. 你会得到一条看起来像这样的线，并且注意到斜率是$\frac{0.5}{1}$。而$w$的值给出了线条的斜率，也就是0.5。

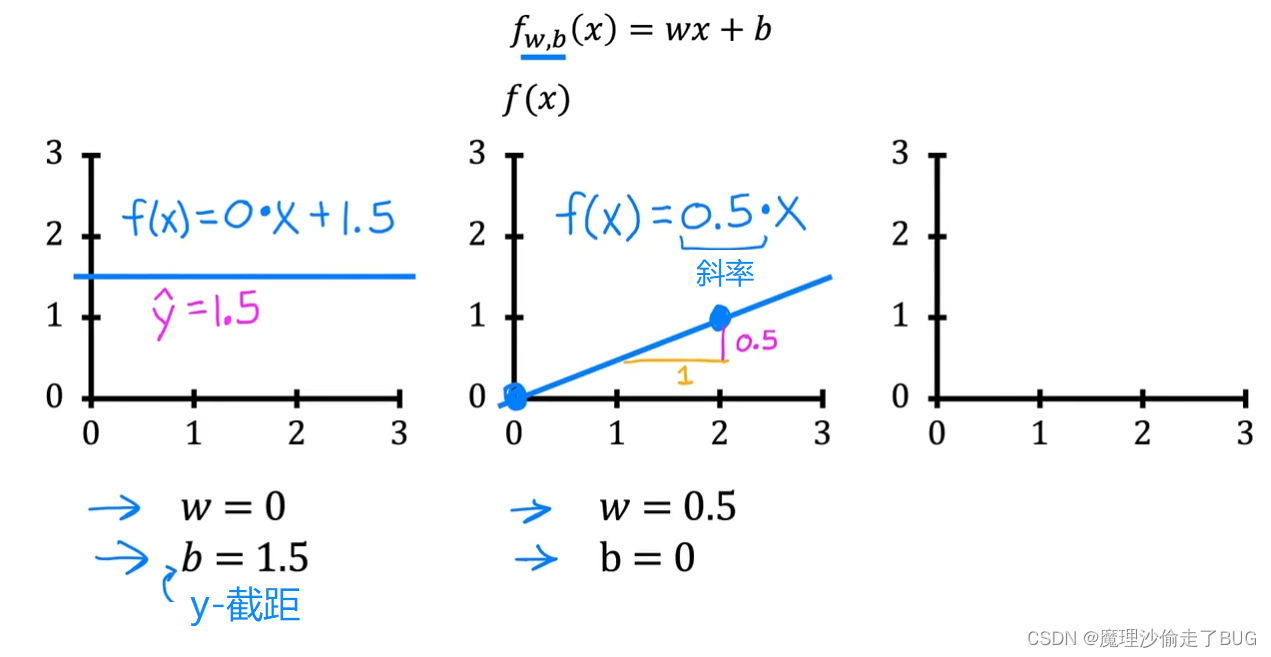
Finally, if w equals 0.5 and b equals 1, then f of x is 0.5 times x plus 1 and when x is 0, then f of x equals b, which is 1 so the line intersects the vertical axis at b, the y intercept. Also when x is 2, then f of x is 2, so the line looks like this. Again, this slope is 0.5 divided by 1 so the value of w gives you the slope which is 0.5.
最后，如果$w=0.5$，$b=1$，那么$f(x)=0.5x+1$. 当$x=0$时，$f(x)=b$，也就是1，因此线条与垂直轴在b处相交，即y截距。此外，当$x=2$时，$f(x)=2$，因此线条呈现如下形状。同样，这个斜率是$\frac{0.5}{1}$，因此$w$的值给出了斜率，即0.5。

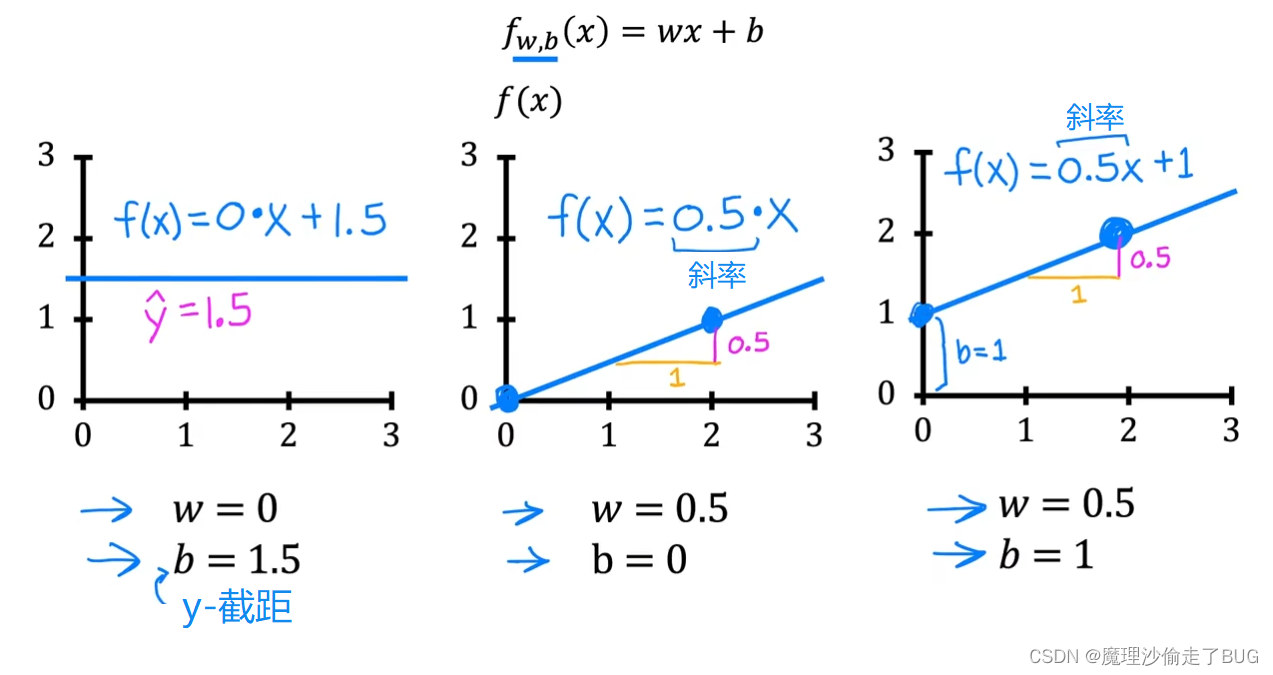
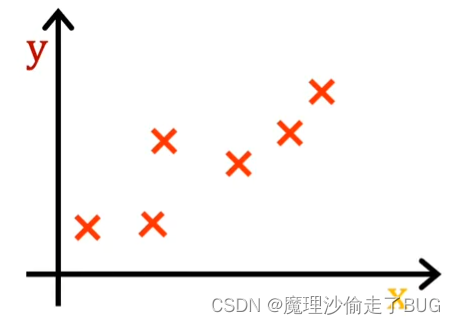
Recall that you have a training set like the one shown here. With linear regression, what you want to do is to choose values for the parameters w and b so that the straight line you get from the function f somehow fits the data well. Like maybe this line shown here.
回想一下，你有一个类似于这里展示的训练集。

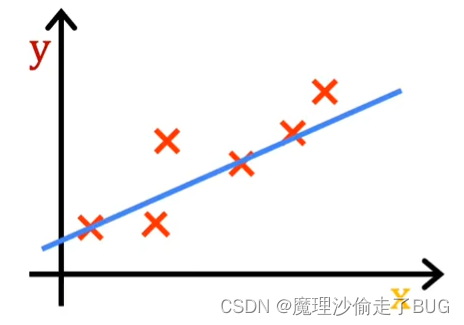
在线性回归中，你希望选择参数$w$和$b$的值，使得由函数f生成的直线与数据相拟合得较好，就像这里展示的这条线一样。

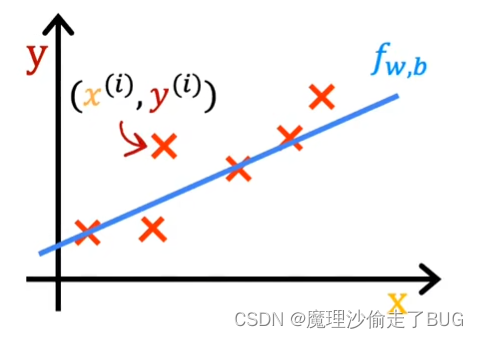
When I see that the line fits the data visually, you can think of this to mean that the line defined by f is roughly passing through or somewhere close to the training examples as compared to other possible lines that are not as close to these points. Just to remind you of some notation, a training example like this point here is defined by x superscript i, y superscript i where y is the target.
当我看到直线在视觉上与数据拟合时，你可以这样理解，相对于其他可能不太接近这些点的直线，由函数$f$所定义的直线大致通过或接近于训练样本组成的集合。再次提醒一下符号的表示，像这个点一样的训练样本被定义为$x^{(i)}$、$y^{(i)}$，其中$y$是目标值。

For a given input x^i, the function f also makes a predictive value for y and a value that it predicts to y is y hat i shown here. For our choice of a model f of x^i is w times x^i plus b. Stated differently, the prediction y hat i is f of wb of x^i where for the model we’re using f of x^i is equal to wx^i plus b.
对于给定的输入$x^{(i)}$，函数$f$还会对$y$有一个预测的值，表示为${\hat{y}}^{(i)}$。我们选择的模型$f$对于输入$x^{(i)}$的表达式是$f(x)=w{x}^{(i)}+b$. 换句话说，预测值${\hat{y}}^{(i)}$可以表示为${\hat{y}}^{(i)}=f_{w,b}(x^{(i)})$，其中对于我们使用的模型，$f_{w,b}(x^{(i)})=w{x}^{(i)}+b$.

Now the question is how do you find values for w and b so that the prediction y hat i is close to the true target y^i for many or maybe all training examples x^i, y^i. To answer that question, let’s first take a look at how to measure how well a line fits the training data. To do that, we’re going to construct a cost function.
现在的问题是如何找到参数$w$和$b$的值，使得对于许多或者所有的训练样本$x^{(i)}$、$y^{(i)}$，预测值${\hat{y}}^{(i)}$与真实目标值$y^{(i)}$接近。为了回答这个问题，让我们首先看一下如何衡量一条直线对训练数据的拟合程度。为此，我们将构建一个代价函数（cost function）。

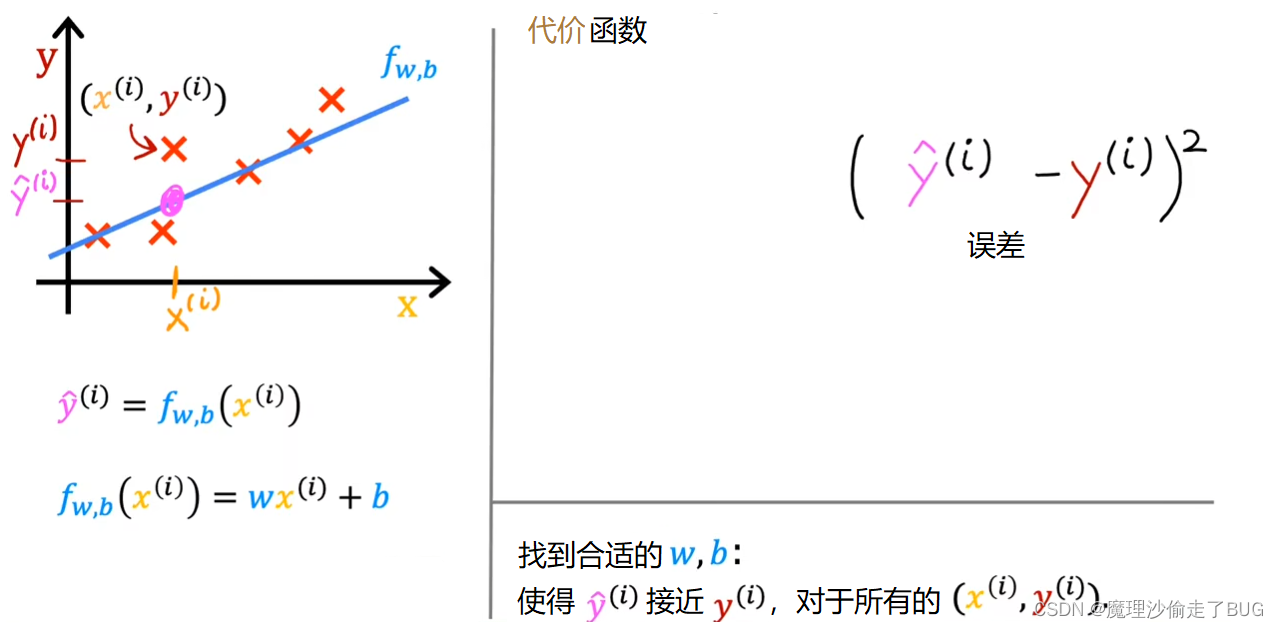
The cost function takes the prediction y hat and compares it to the target y by taking y hat minus y. This difference is called the error, we’re measuring how far off to prediction is from the target. Next, let’s computes the square of this error. Also, we’re going to want to compute this term for different training examples i in the training set. When measuring the error, for example i, we’ll compute this squared error term.
代价函数将预测值$\hat{y}$与真实的目标值$y$进行比较，通过计算$\hat{y}-y$得到一个差值。这个差值被称为误差（error），我们测量了预测值与目标值之间的偏差大小。接下来，我们会计算这个误差的平方。同时，对于训练集中的第$i$个样本，我们需要计算每个样本的预测值和真实值之间的误差。当我们计算误差时，比如，对于第$i$个训练样本，我们将计算这个平方误差项${\hat{y}}^{(i)}-y^{(i)}$.

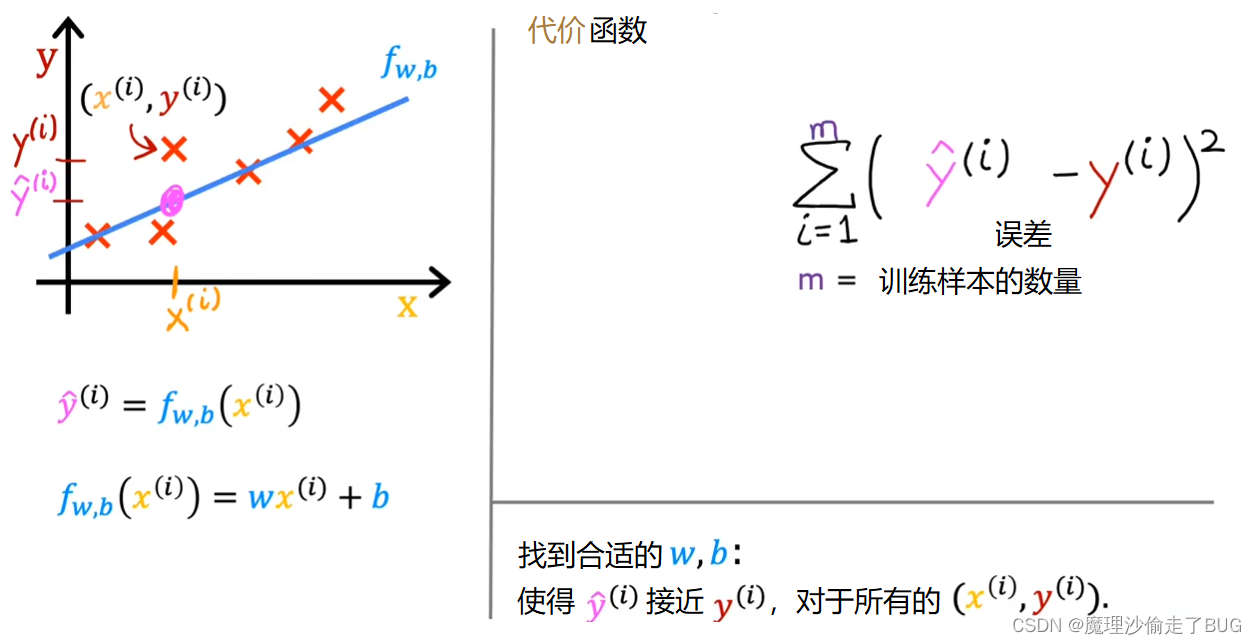
Finally, we want to measure the error across the entire training set. In particular, let’s sum up the squared errors like this. We’ll sum from i equals 1,2, 3 all the way up to m and remember that m is the number of training examples, which is 47 for this dataset.
最后，我们希望衡量整个训练集上的误差。具体而言，我们将按照如下方式将这些平方误差求和，即$\sum _{i=1}^m({\hat{y}}^{(i)}-y^{(i)}{)}^2$，需要记住$m$是训练样本的数量，对于这个数据集来说$m=47$。

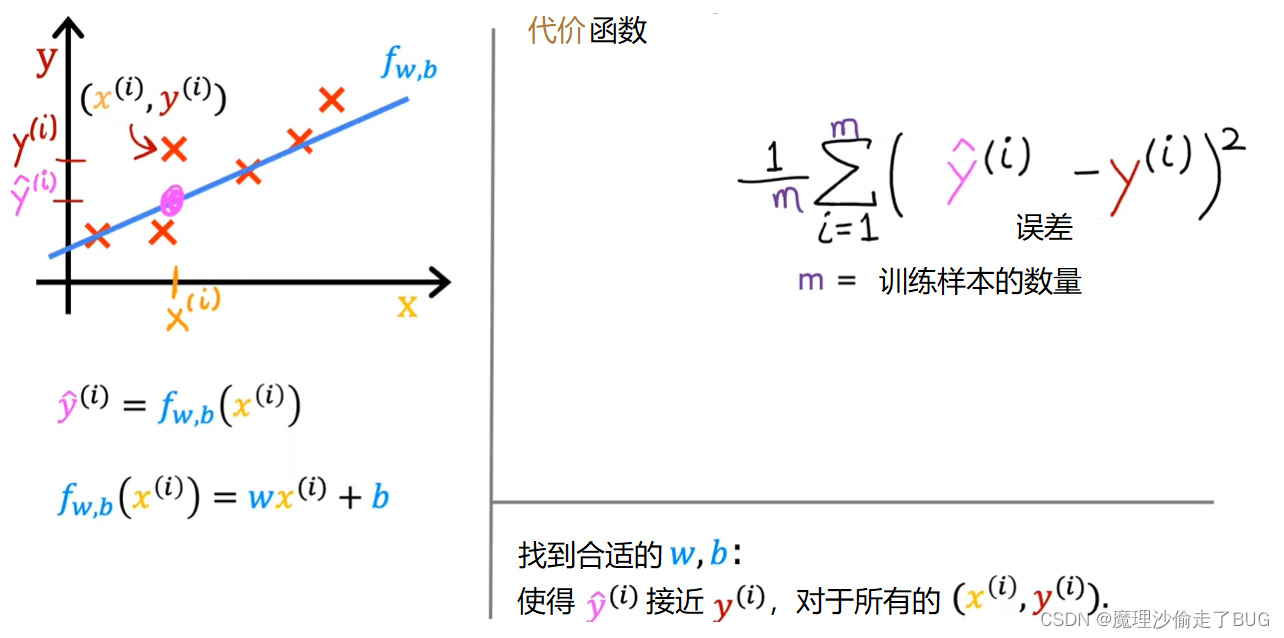
Notice that if we have more training examples m is larger and your cost function will calculate a bigger number. This is summing over more examples. To build a cost function that doesn’t automatically get bigger as the training set size gets larger by convention, we will compute the average squared error instead of the total squared error and we do that by dividing by m like this.
请注意，如果我们有更多的训练样本，即m更大，那么你的代价函数会计算一个更大的数值。这是因为我们对更多的样本进行求和操作。为了构建一个无论训练集大小如何都不会自动增大的代价函数，我们通常计算平均平方误差而不是总平方误差，这可以通过除以$m$来实现，如下所示。

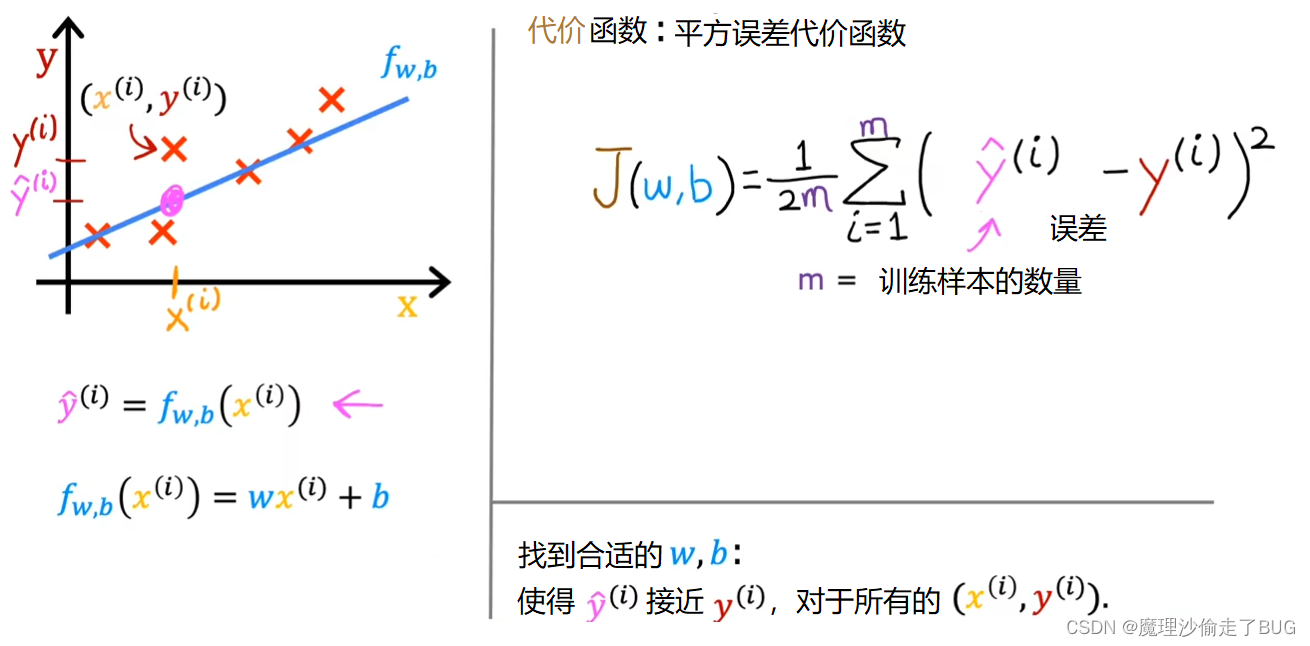
We’re nearly there. Just one last thing. By convention, the cost function that machine learning people use actually divides by 2 times m. The extra division by 2 is just meant to make some of our later calculations look neater, but the cost function still works whether you include this division by 2 or not. This expression right here is the cost function and we’re going to write J of wb to refer to the cost function. This is also called the squared error cost function, and it’s called this because you’re taking the square of these error terms.
我们快要完成了，只剩下最后一点。按照惯例，机器学习中使用的代价函数实际上会除以2倍的m。这额外的除以2只是为了使我们后面的计算更加简洁，但无论是否包括这个除以2，代价函数仍然有效。这个表达式就是代价函数，即$\frac{1}{2m}\sum _{i=1}^m({\hat{y}}^{(i)}-y^{(i)}{)}^2$，我们将用$J(w,b)=\frac{1}{2m}\sum _{i=1}^m({\hat{y}}^{(i)}-y^{(i)}{)}^2$表示损失函数。这个损失函数也被称为平方误差代价函数，因为它对这些误差项取平方。

In machine learning different people will use different cost functions for different applications, but the squared error cost function is by far the most commonly used one for linear regression and for that matter, for all regression problems where it seems to give good results for many applications. Just as a reminder, the prediction y hat is equal to the outputs of the model f at x.
在机器学习中，不同的人会根据不同的应用选择不同的代价函数，但是对于线性回归以及其他许多回归问题来说，平方误差代价函数是最常用的。这个代价函数在许多应用中都能给出良好的结果。提醒一下，预测值${\hat{y}}^{(i)}$等于模型$f$在输入$x$上的输出结果。

We can rewrite the cost function J of wb as 1 over 2m times the sum from i equals 1 to m of f of x^i minus y^i the quantity squared.
我们可以将损失函数$J(w,b)$重写为$J(w,b)=\frac{1}{2m}\sum _{i=1}^m{\left(f(x^{(i)})-y^{(i)}\right)}^2$

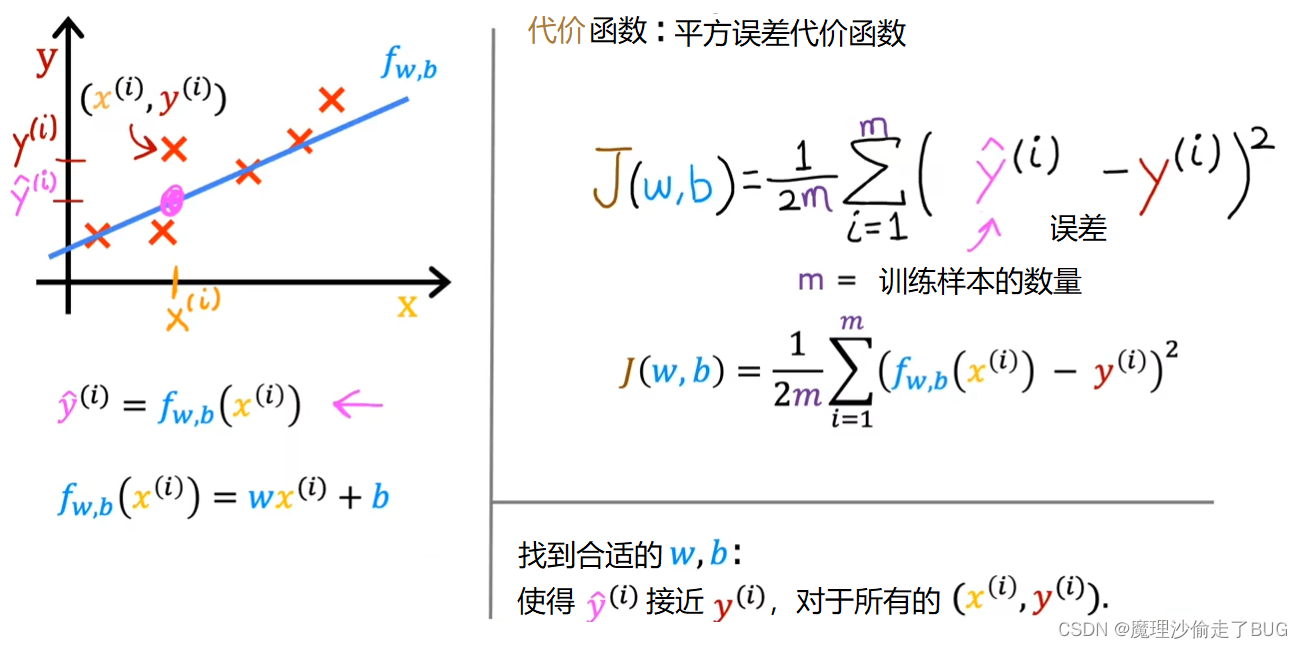
Eventually we’re going to want to find values of w and b that make the cost function small.
最后，我们要找到使代价函数最小的$w$和$b$.

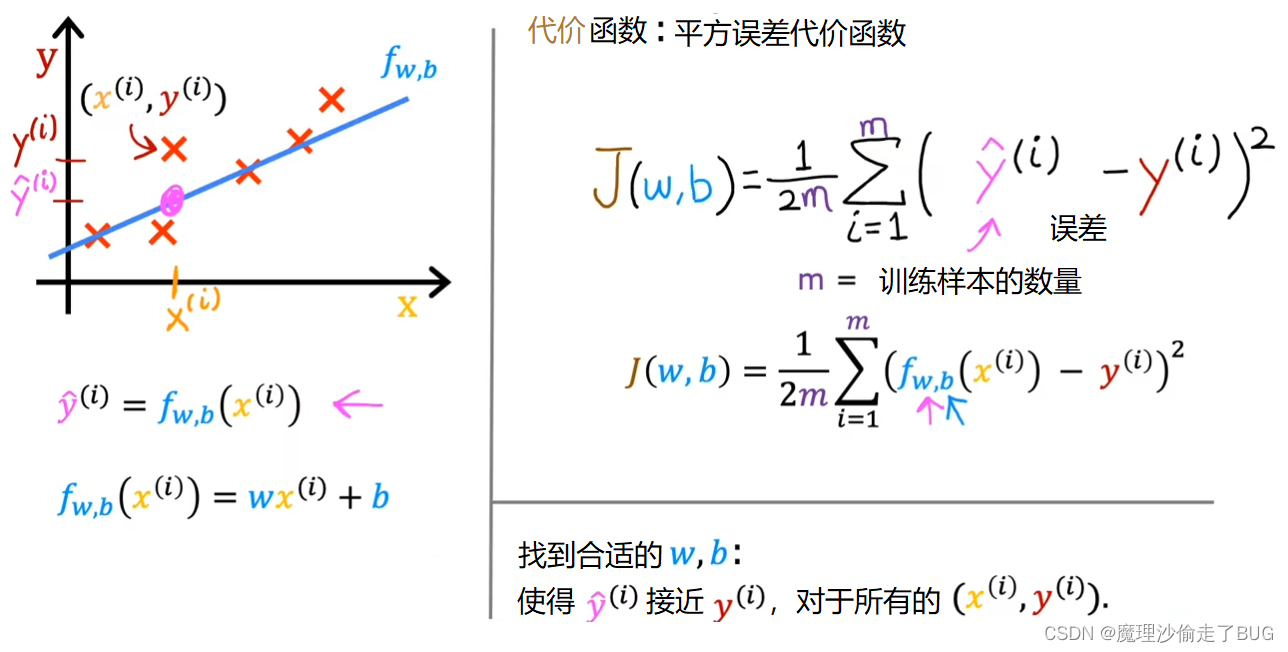
But before going there, let’s first gain more intuition about what J of wb is really computing.
在深入探讨之前，让我们首先更好地理解$J(w,b)$到底在计算什么。

At this point you might be thinking we’ve done a whole lot of math to define the cost function. But what exactly is it doing? Let’s go on to the next video where we’ll step through one example of what the cost function is really computing that I hope will help you build intuition about what it means if J of wb is large versus if the cost j is small. Let’s go on to the next video.
到目前为止，你可能正在想我们已经进行了很多数学推导来定义代价函数。但是，它到底是在做什么呢？让我们继续看下一个视频，在下一个视频中，我们将通过一个例子详细解释损失函数到底在计算什么，希望能帮助你对$J(w,b)$的大或小的含义建立直觉。让我们继续观看下一个视频。