排序算法汇总
常用十大排序算法_calm_G的博客-CSDN博客
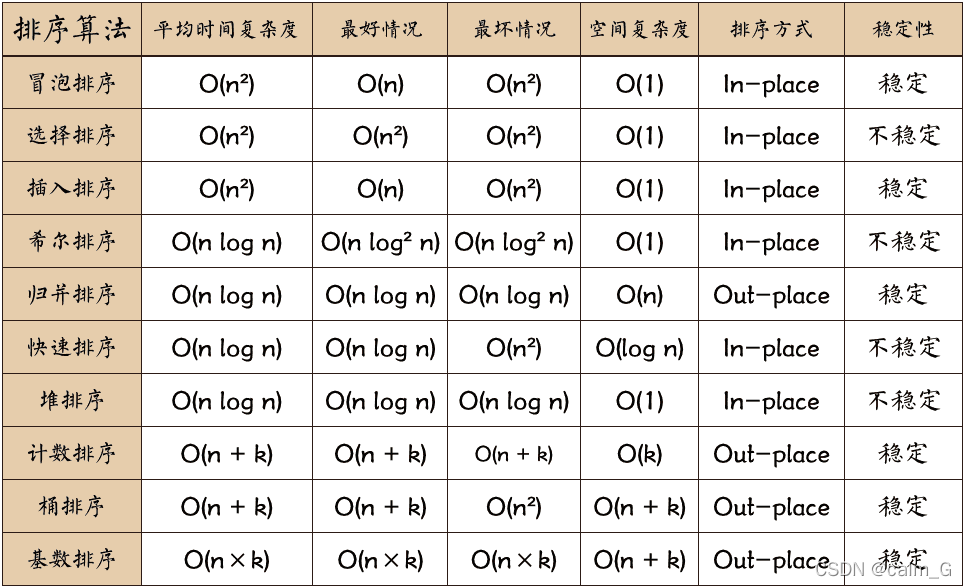
以下动图参考 十大经典排序算法 Python 版实现(附动图演示) - 知乎
冒泡排序
排序过程如下图所示:

- 比较相邻的元素。如果第一个比第二个大,就交换他们两个。
- 对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对。这步做完后,最后的元素会是最大的数。
- 针对所有的元素重复以上的步骤,除了最后一个。
- 持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较。
// arr: 需要排序的数组; length: 数组长度
//注: int cnt = sizeof(a) / sizeof(a[0]);获取数组长度
void BubbleSort(int arr[], int length)
{
for (int i = 0; i < length; i++)
{
for (int j = 0; j < length - i - 1; j++)
{
if (arr[j] > arr[j + 1])
swap(arr[j],arr[j+1]);
}
}
}选择排序
排序过程如下图所示:

- 在未排序序列中找到最小(大)元素,存放到排序序列的起始位置
- 从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾
- 以此类推,直到所有元素均排序完毕
- 时间负复杂度:O(n^2),空间O(1),非稳定排序,原地排序
void selectSort(vector<int>& nums) {
int len = nums.size();
int minIndex = 0;
for (int i = 0; i < len; ++i) {
minIndex = i;
for (int j = i + 1; j < len; ++j) {
if (nums[j] < nums[minIndex]) minIndex = j;
}
swap(nums[i], nums[minIndex]);
}
}
插入排序
排序过程如下图所示:

从第一个元素开始,该元素可以认为已经被排序
取出下一个元素,在已经排序的元素序列中从后向前扫描
如果该元素(已排序)大于新元素,将该元素移到下一位置
重复步骤3,直到找到已排序的元素小于或者等于新元素的位置
将新元素插入到该位置后
重复步骤2~5
void insertionSort(vector<int>& a, int n) {//{ 9,1,5,6,2,3 }
for (int i = 1; i < n; ++i) {
if (a[i] < a[i - 1]) { //若第i个元素大于i-1元素,直接插入。小于的话,移动有序表后插入
int j = i - 1;
int x = a[i]; //复制为哨兵,即存储待排序元素
//a[i] = a[i - 1]; //先后移一个元素,可以不要这一句,跟循环里面的功能重复了
while (j >= 0 && x < a[j]) { //查找在有序表的插入位置,还必须要保证j是>=0的 因为a[j]要合法
a[j + 1] = a[j];
j--; //元素后移
}
a[j + 1] = x; //插入到正确位置
}
}
}快速排序
排序过程如下图所示:
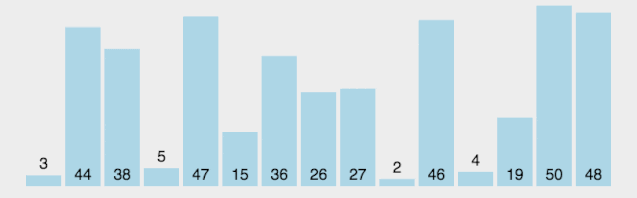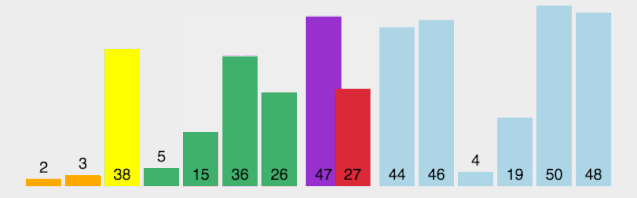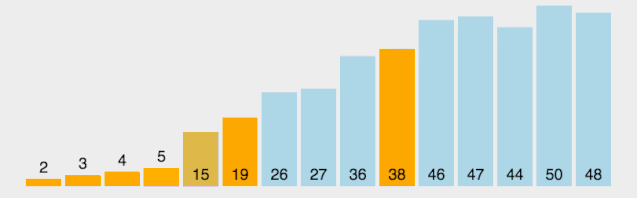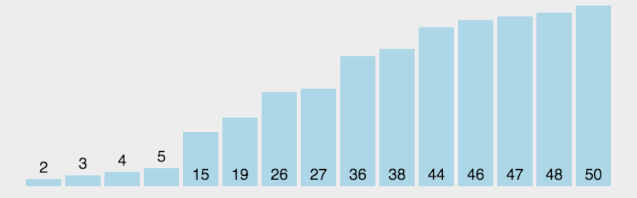
动图看起来有点复杂,下面放一个分解图https://blog.csdn.net/qq_38082146/article/details/115453732
我们以[ 8,2,5,0,7,4,6,1 ]这组数字为例来进行演示
首先,我们随机选择一个基准值(虽然图中选择了随机元素,但是一般上会以第一个元素为基准值):
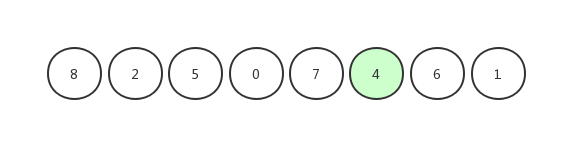
与其他元素依次比较,大的放右边,小的放左边:
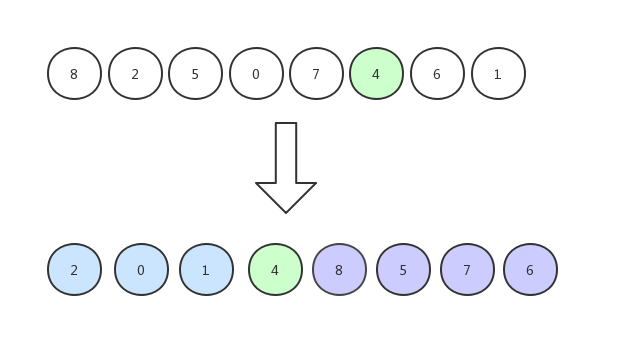
然后我们以同样的方式排左边的数据:
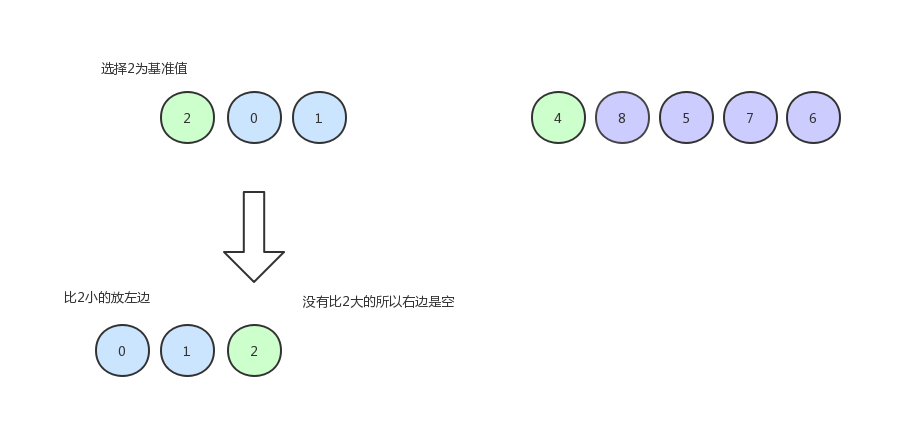
继续排 0 和 1 :
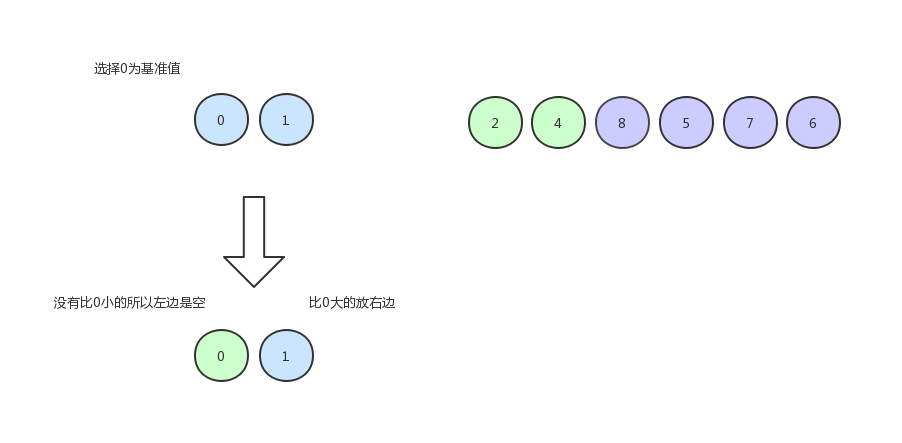
由于只剩下一个数,所以就不用排了,现在的数组序列是下图这个样子:
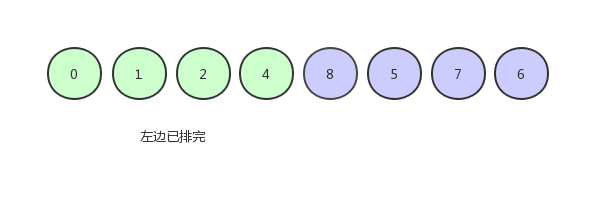
右边以同样的操作进行,即可排序完成。
1、选取第一个数为基准
2、将比基准小的数交换到前面,比基准大的数交换到后面
3、对左右区间重复第二步,直到各区间只有一个数
void quickSort(vector<int>&numbers, int low, int high) {
// numbers = {10,8,4,6,9,10,123,6,2,14,3,8,5};
if (low >= high) return;
int first = low, last = high, key = numbers[low];
cout << low << " " << high << " "<<key << endl;
for (int i = 0; i < numbers.size(); ++i) {
cout << numbers[i] << " ";
}
cout << endl;
while (first < last) {
//从后往前找比他小的放前面,从前往后找比他大的放在后面,
//以第一个数为基准,必须先从后往前走,再从前往后走
while (first < last && numbers[last] >= key)
last--;
if (first < last) numbers[first++] = numbers[last];
while (first < last && numbers[first] <= key)
first++;
if (first < last) numbers[last--] = numbers[first];
}
numbers[first] = key;
cout << "the index " << first << " value " << key << endl;
quickSort(numbers, low, first - 1);
quickSort(numbers, first + 1, high);
}
希尔排序
排序过程如下图所示:

希尔排序是插入排序的一种变种。无论是插入排序还是冒泡排序,如果数组的最大值刚好是在第一位,要将它挪到正确的位置就需要 n - 1 次移动。
也就是说,原数组的一个元素如果距离它正确的位置很远的话,则需要与相邻元素交换很多次才能到达正确的位置,这样是相对比较花时间了。
希尔排序就是为了加快速度简单地改进了插入排序,交换不相邻的元素以对数组的局部进行排序。
希尔排序的思想是采用插入排序的方法,先让数组中任意间隔为 h 的元素有序,刚开始 h 的大小可以是 h = n / 2,接着让 h = n / 4,让 h 一直缩小,当 h = 1 时,也就是此时数组中任意间隔为1的元素有序,此时的数组就是有序的了。
void shellSortCore(vector<int>& nums, int gap, int i) {
int inserted = nums[i];
int j;
// 插入的时候按组进行插入
for (j = i - gap; j >= 0 && inserted < nums[j]; j -= gap) {
nums[j + gap] = nums[j];
}
nums[j + gap] = inserted;
}
void shellSort(vector<int>& nums) {
int len = nums.size();
//进行分组,最开始的时候,gap为数组长度一半
for (int gap = len / 2; gap > 0; gap /= 2) {
//对各个分组进行插入分组
for (int i = gap; i < len; ++i) {
//将nums[i]插入到所在分组正确的位置上
shellSortCore(nums,gap,i);
}
}
}归并排序
排序过程如下图所示:

1、把长度为n的输入序列分成两个长度为n/2的子序列;
2、对这两个子序列分别采用归并排序;
3、 将两个排序好的子序列合并成一个最终的排序序列。
void mergeSortCore(vector<int>& data, vector<int>& dataTemp, int low, int high) {
if (low >= high) return;
int len = high - low, mid = low + len / 2;
int start1 = low, end1 = mid, start2 = mid + 1, end2 = high;
mergeSortCore(data, dataTemp, start1, end1);
mergeSortCore(data, dataTemp, start2, end2);
int index = low;
while (start1 <= end1 && start2 <= end2) {
dataTemp[index++] = data[start1] < data[start2] ? data[start1++] : data[start2++];
}
while (start1 <= end1) {
dataTemp[index++] = data[start1++];
}
while (start2 <= end2) {
dataTemp[index++] = data[start2++];
}
for (index = low; index <= high; ++index) {
data[index] = dataTemp[index];
}
}
void mergeSort(vector<int>& data) {
int len = data.size();
vector<int> dataTemp(len, 0);
mergeSortCore(data, dataTemp, 0, len - 1);
}堆排序
分为创建堆和堆排序两个部分
创建堆(这里假定是大根堆)时,要保证每个父节点的值比左右子节点的值大
当每次堆排序完成后,最顶端的即是当前堆的最大值,随后可以将堆的最大值与堆的倒数第一个元素互换,因为此时当前最大值已经完成排序,将其赶出堆内,堆的size减1,剩下的元素进行堆重构。
堆重构的过程就是维持堆每个父节点的值大于左右子节点值的过程
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
//i位置的数,向上调整大根堆
void heapInsert(vector<int>& arr, int i)
{
while (arr[i] > arr[(i - 1) / 2]) //子节点比父节点大
{
swap(arr[i], arr[(i - 1) / 2]);
i = (i - 1) / 2;
}
}
//i位置的数发生了变化,又想维持住大根堆的结构
void heapify(vector<int>& arr, int i, int size)
{
int l = 2 * i + 1; //左孩子
while (l < size)
{
int best = l + 1 < size && arr[l + 1] > arr[l] ? l + 1 : l;
best = arr[best] > arr[i] ? best : i;
if (best == i)
break;
swap(arr[i], arr[best]);
i = best;
l = 2 * i + 1;
}
}
//从顶到底建立大根堆
//依次弹出堆内的最大值,并重新排好序
void heapSort(vector<int>& arr)
{
int size = arr.size();
for (int i = 0; i < size; i++) //建立大根堆
{
heapInsert(arr, i);
}
while (size > 1)
{
swap(arr[0], arr[size - 1]);
size--;
cout<< arr[size] <<endl;
heapify(arr, 0, size);
}
}
int main()
{
vector<int> arr = { 3,2,1,5,6,4 };
heapSort(arr);
}
计数排序
计数排序用于元素大小范围有限的数值排序。
- 如果 k(待排数组的最大值) 过大则会引起较大的空间复杂度,一般是用来排序 0 到 100 之间的数字的最好的算法,但是它不适合按字母顺序排序人名。
统计小于等于该元素值的元素的个数i,于是该元素就放在目标数组的索引i位(i≥0)

- 找出待排序的数组中最大和最小的元素;
- 统计数组中每个值为 i 的元素出现的次数,存入数组 C 的第 i 项;
- 对所有的计数累加(从 C 中的第一个元素开始,每一项和前一项相加);
- 向填充目标数组:将每个元素 i 放在新数组的第 C[i] 项,每放一个元素就将 C[i] 减去 1
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
// 计数排序
void CountSort(vector<int>& vecRaw, vector<int>& vecObj)
{
// 确保待排序容器非空
if (vecRaw.size() == 0)
return;
// 使用 vecRaw 的最大值 + 1 作为计数容器 countVec 的大小
int vecCountLength = (*max_element(begin(vecRaw), end(vecRaw))) + 1;
vector<int> vecCount(vecCountLength, 0);
// 统计每个键值出现的次数
for (int i = 0; i < vecRaw.size(); i++)
vecCount[vecRaw[i]]++;
// 后面的键值出现的位置为前面所有键值出现的次数之和
for (int i = 1; i < vecCountLength; i++)
vecCount[i] += vecCount[i - 1];
// 将键值放到目标位置
for (int i = vecRaw.size(); i > 0; i--) // 此处逆序是为了保持相同键值的稳定性
vecObj[--vecCount[vecRaw[i - 1]]] = vecRaw[i - 1];
}
int main()
{
vector<int> vecRaw = { 0,5,7,9,6,3,4,5,2,8,6,9,2,1 };
vector<int> vecObj(vecRaw.size(), 0);
CountSort(vecRaw, vecObj);
for (int i = 0; i < vecObj.size(); ++i)
cout << vecObj[i] << " ";
cout << endl;
return 0;
}桶排序
排序过程如下图所示:

- 设置一个定量的数组当作空桶子。
- 寻访序列,并且把项目一个一个放到对应的桶子去。
- 对每个不是空的桶子进行排序。
- 从不是空的桶子里把项目再放回原来的序列中。
#include<stdio.h>
int main() {
int book[1001],i,j,t;
//初始化桶数组
for(i=0;i<=1000;i++) {
book[i] = 0;
}
//输入一个数n,表示接下来有n个数
scanf("%d",&n);
for(i = 1;i<=n;i++) {
//把每一个数读到变量中去
scanf("%d",&t);
//计数
book[t]++;
}
//从大到小输出
for(i = 1000;i>=0;i--) {
for(j=1;j<=book[i];j++) {
printf("%d",i);
}
}
getchar();getchar();
//getchar()用来暂停程序,以便查看程序输出的内容
//也可以用system("pause");来代替
return 0;
}
基数排序

- 取得数组中的最大数,并取得位数;
- arr为原始数组,从最低位开始取每个位组成radix数组;
- 对radix进行计数排序(利用计数排序适用于小范围数的特点)
int maxbit(int data[], int n) //辅助函数,求数据的最大位数
{
int maxData = data[0]; ///< 最大数
/// 先求出最大数,再求其位数,这样有原先依次每个数判断其位数,稍微优化点。
for (int i = 1; i < n; ++i)
{
if (maxData < data[i])
maxData = data[i];
}
int d = 1;
int p = 10;
while (maxData >= p)
{
//p *= 10; // Maybe overflow
maxData /= 10;
++d;
}
return d;
}
void radixsort(int data[], int n) //基数排序
{
int d = maxbit(data, n);
int *tmp = new int[n];
int *count = new int[10]; //计数器
int i, j, k;
int radix = 1;
for(i = 1; i <= d; i++) //进行d次排序
{
for(j = 0; j < 10; j++)
count[j] = 0; //每次分配前清空计数器
for(j = 0; j < n; j++)
{
k = (data[j] / radix) % 10; //统计每个桶中的记录数
count[k]++;
}
for(j = 1; j < 10; j++)
count[j] = count[j - 1] + count[j]; //将tmp中的位置依次分配给每个桶
for(j = n - 1; j >= 0; j--) //将所有桶中记录依次收集到tmp中
{
k = (data[j] / radix) % 10;
tmp[count[k] - 1] = data[j];
count[k]--;
}
for(j = 0; j < n; j++) //将临时数组的内容复制到data中
data[j] = tmp[j];
radix = radix * 10;
}
delete []tmp;
delete []count;
}