1. 树结构概述

现实生活中，具有很多层次关系：归纳为一种树状结构（一种层级结构）

2. 二叉树

2.2 二叉树分类

3.1.2.1 满二叉树

高度为4的满二叉树

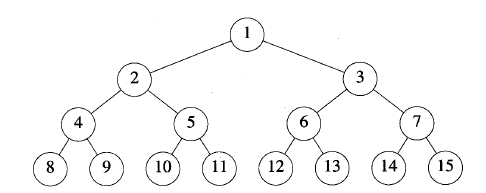
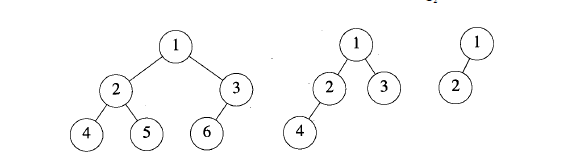
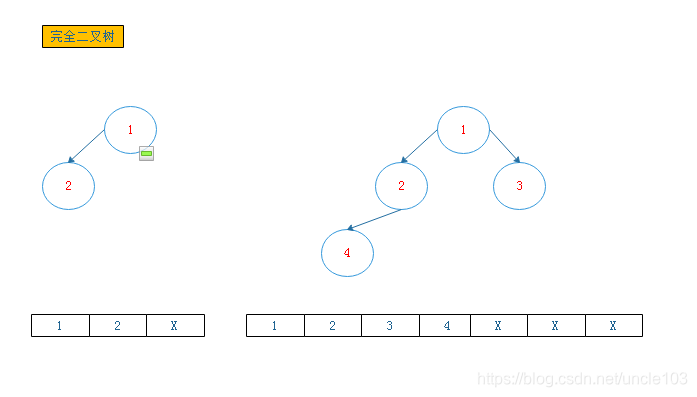
3.1.2.2 完全二叉树

• 若一棵二叉树至多只有最下面两层的结点的度数可以小于2，并且最下层的结点都集中在该层最左边的若干位置上，则此二叉树为完全二叉树。
  

3.1.3 二叉树描述

数组描述：
高度为h的满二叉树，节点数为2^n -1：每一个节点的编号即为数组存储的下标

3.1.3.1 数组描述

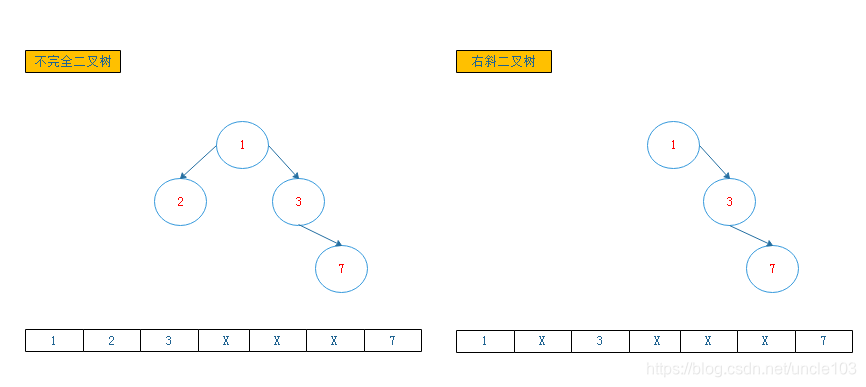
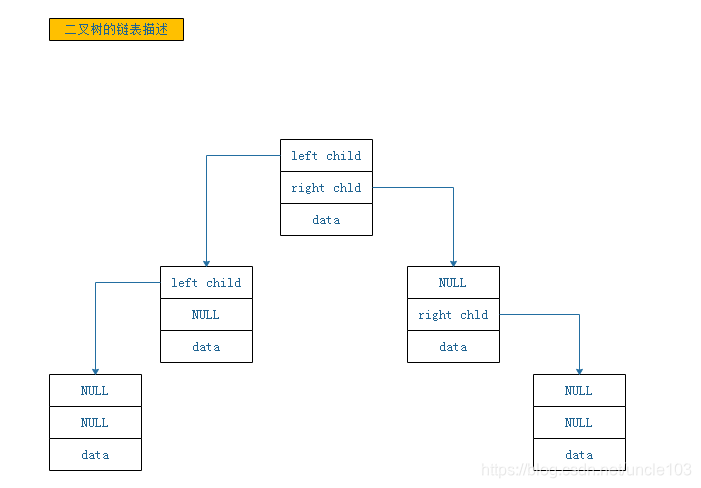
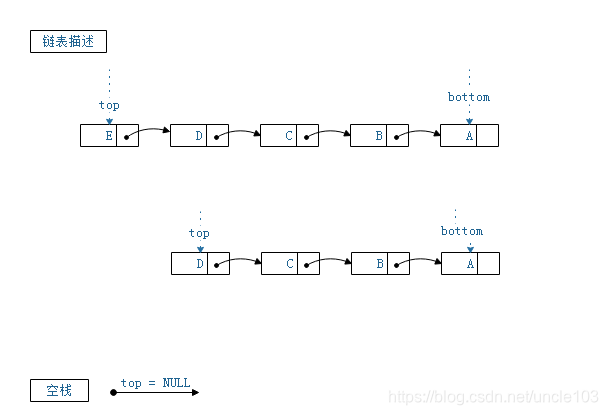
3.1.3.2 链表描述

使用链表描述二叉树十分方便，通过指针实现

2.1 二叉树应用

2.1.1 数学表达式

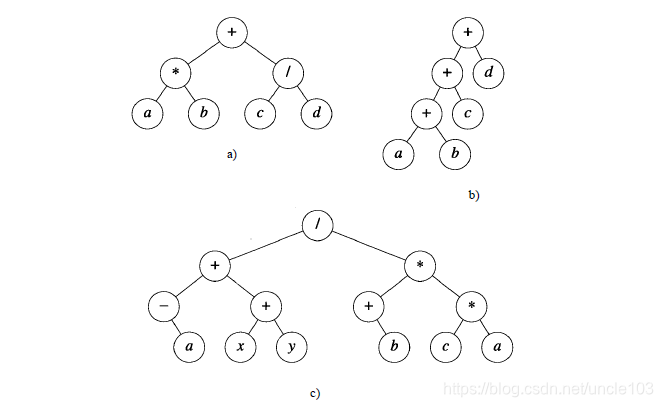
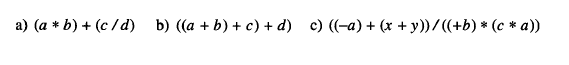
3.1.4 最大/最小 问题

最大树/最小树定义：
每个节点都大于（小于）或者等于其子节点的二叉树叫做最大（最小）树

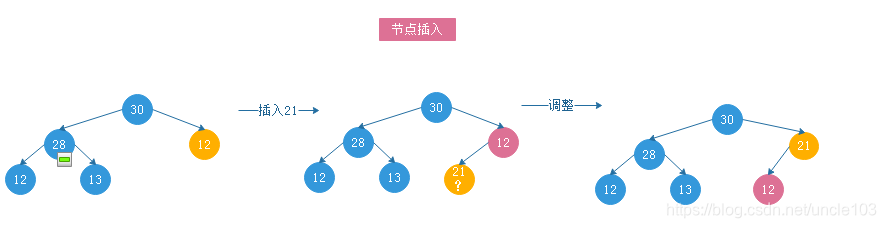
3.1.4.1 最大堆

约束条件：完全树形态的最大树
节点插入 示例：

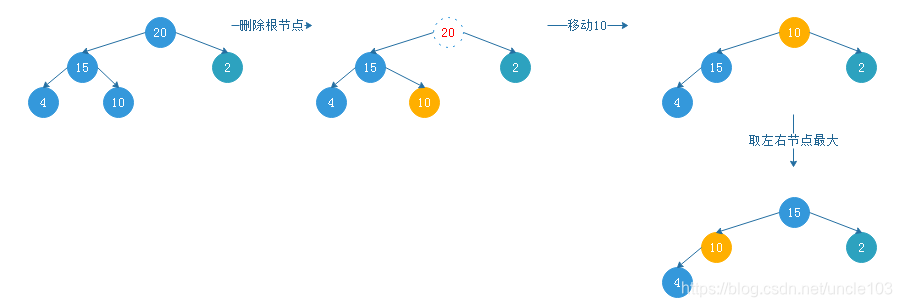
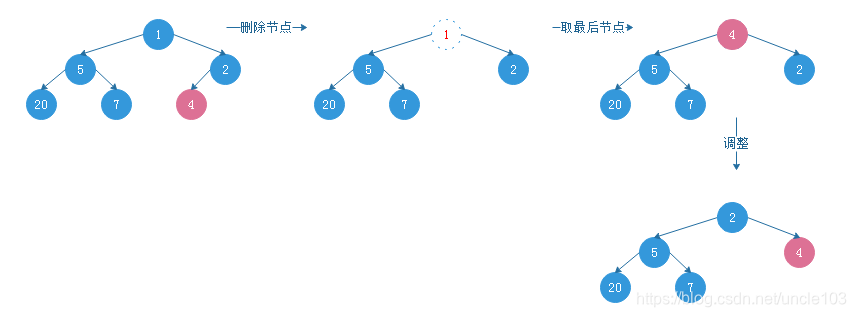
节点删除 示例：

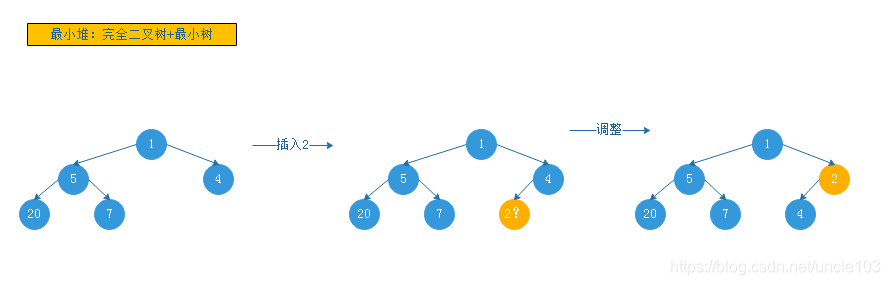
3.1.4.2 最小堆

约束条件：完全树形态的最小树

3.1.4.3 最大/最小 高度优先左高树

约束条件：任意节点左子树高度大于右子树的最大或者最小树
节点的高度：

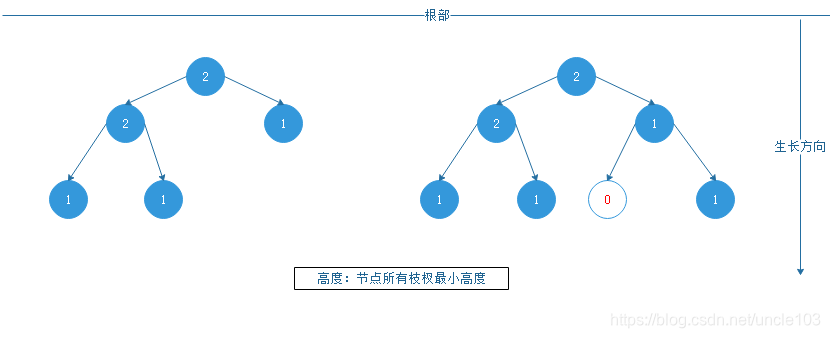
高度优先左高树约束条件：

• 左子树高度大于右子树高度

最大高度优先左高树合并

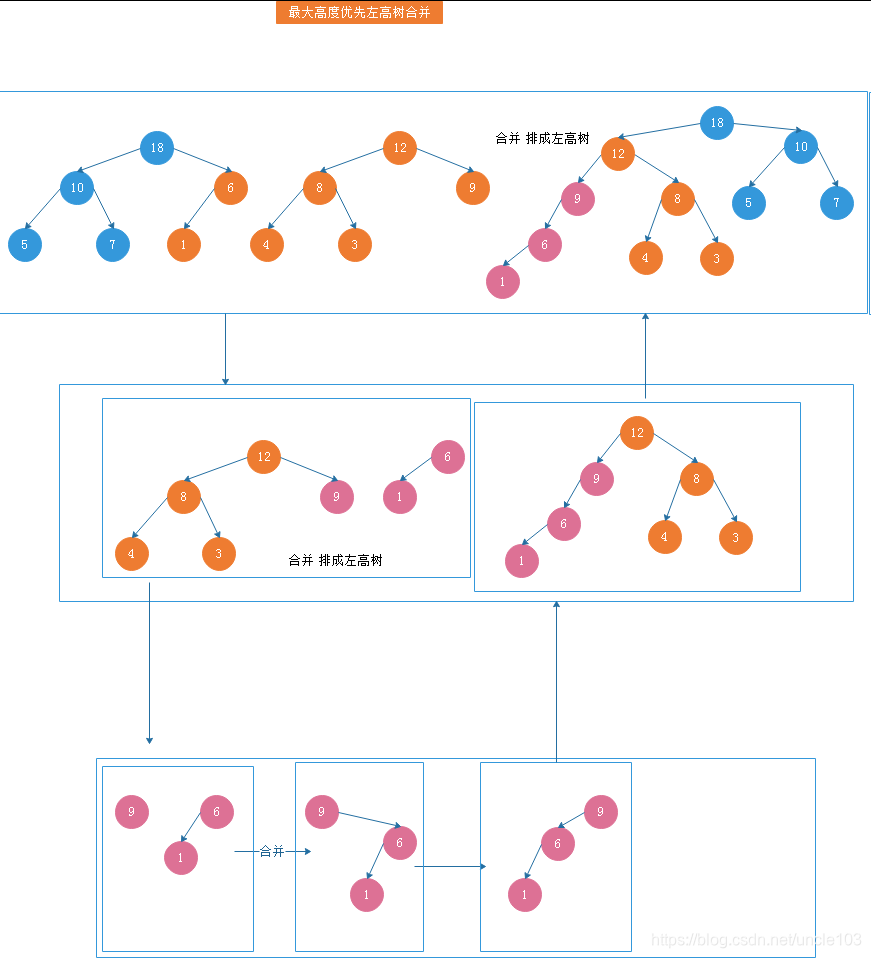
3.1.4.4 最大/最小 重量优先左高树

节点的重量：

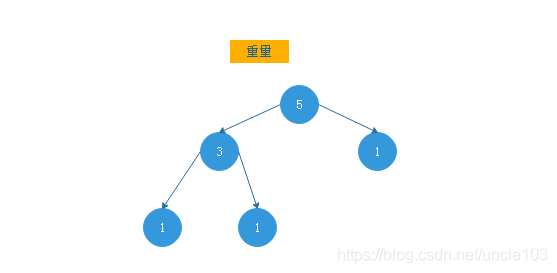
3.1.5 输赢问题

3.1.5.1 赢者树

赢者树约束条件：

• 完全二叉树（推荐，也可以不是）
• 外部节点为n，内部节点为n-1（内部节点用于记录胜利的外部节点）

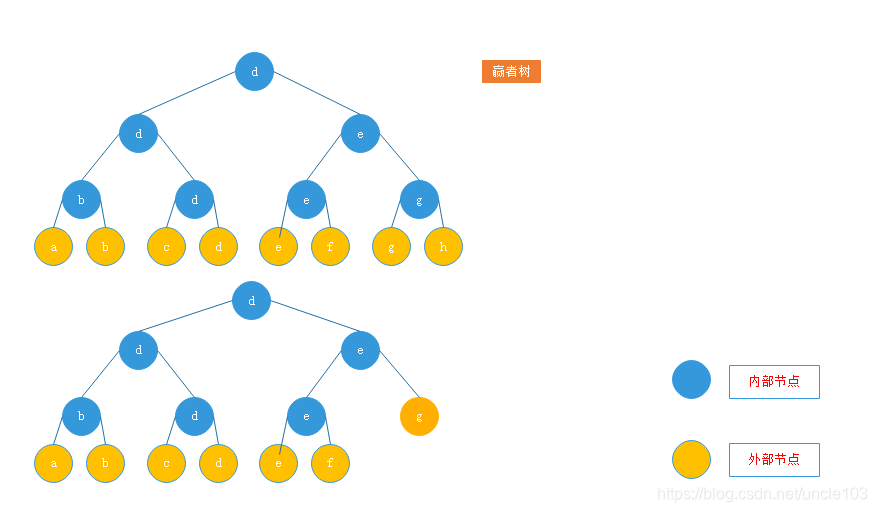
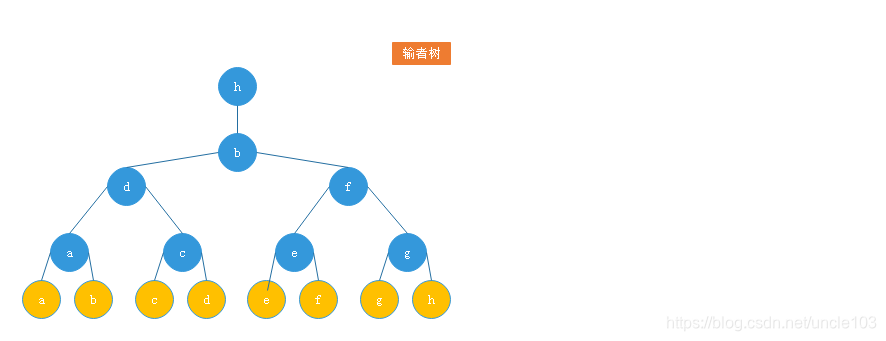
3.1.5.2 输者树

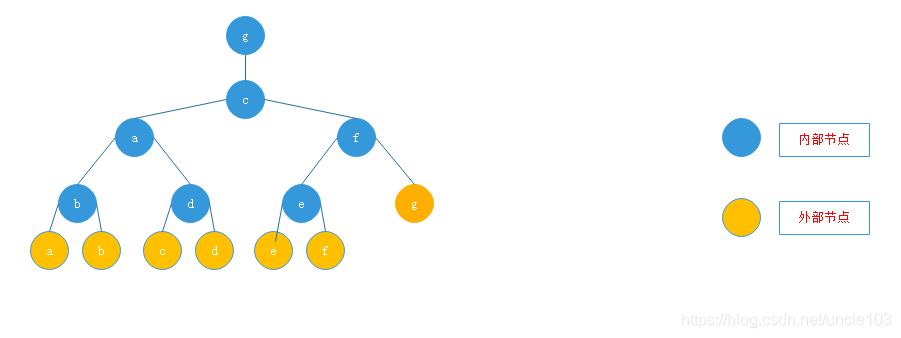
3.1.5 搜索问题

3.1.5.1 二叉搜索树

约束条件：

• 每个节点都有关键值，并且都是唯一的（无重复）
• 对于任意节点，左节点小于根节点，右节点大于根节点
• 子树也是二叉搜索树

节点插入：
查询时，查询节点关键值小于根节点在左子树去找，否则在右子树找（依次递归）

节点删除包括三种情况：
节点为叶节点、节点有一个非空子树，节点有两个非空子树；

• 叶节点删除可以直接删除叶节点即可，是节点插入的逆向操作

• 节点有一个非空子树
  分成两种情况处理
  

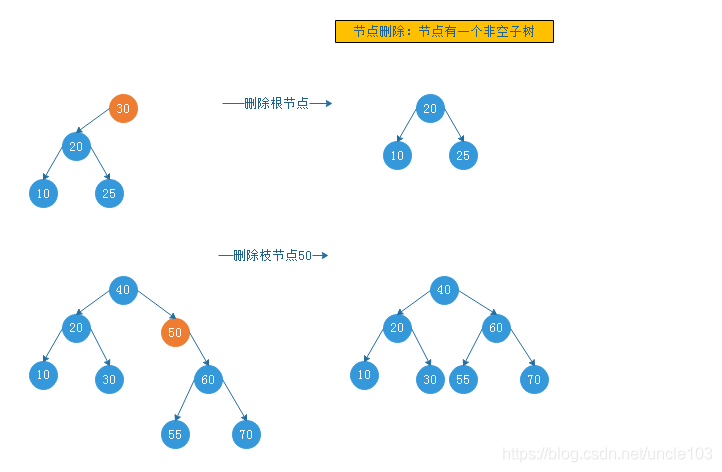
• 节点有两个非空子树
  把左子树最大节点或者右子树最小节点移动到被删除节点即可

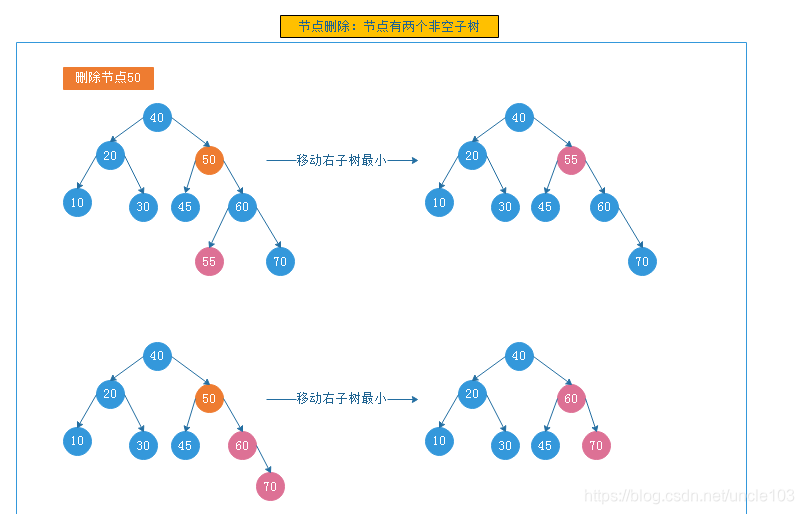
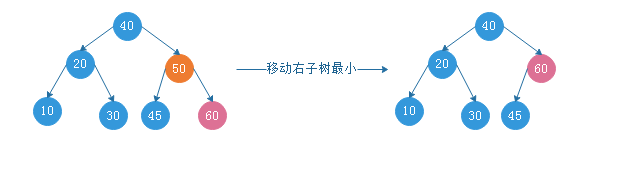或者移动左子树最大的节点

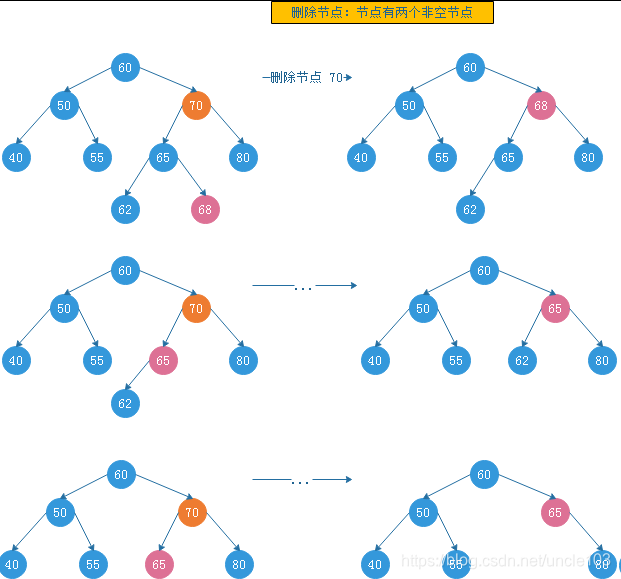
3.1.5.2 AVL树

对于二叉树搜索树，形状为左斜或者右斜二叉树时，搜索的任意节点其复杂度上限可以表示为O(n)，n表示为二叉树节点数目

• 定义 [平衡树]
  当确定搜索树的高度总是O ( l o gn)时，能够保证每个搜索树操作所占用的时间为O( l o gn),高度为O( l o gn)的树称为平衡树（balanced tree）

AVL树是一种平衡树
约束条件：
空二叉树是AV L树；
如果T是一棵非空的二叉树，TL 和TR 分别是其左子树和右子树，那么当T满足以下条件时，T是一棵AV L树：

1. TL 和TR 是AV L树；
2. | hL - hR |≤1, hL 和hR 分别是左子树和右子树的高度。

AVL树图示

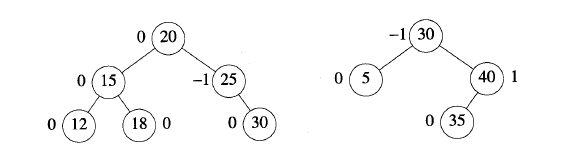
AVL树搜索
AVL树插入
AVL树删除

3.1.5.3 红黑树

红黑树是一种平衡树

红黑树约束条件：
R B 1：根节点和所有外部节点的颜色是黑色。
R B 2：根至外部节点途中没有连续两个节点的颜色是红色。
R B 3：所有根至外部节点的路径上都有相同数目的黑色节点。

红黑树搜索

红黑树插入

红黑树删除

3.1.5.4 m杈搜索树

3.1.5.4.1 m杈搜索树

m杈搜索树

3.1.5.4.2 m序B-树

m序 B-树

4 图

图简介