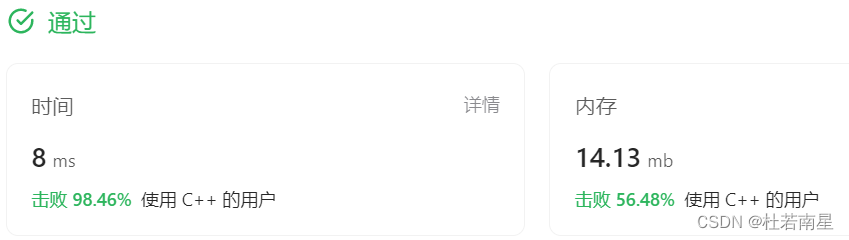
第18节
题目1:汉诺塔问题(变体)
体系学习班18节有讲暴力递归的汉诺塔原题。
给定一个数组arr,长度为N,arr中的值只有1,2,3三种
arr[i] == 1,代表汉诺塔问题中,从上往下第i个圆盘目前在左
arr[i] == 2,代表汉诺塔问题中,从上往下第i个圆盘目前在中
arr[i] == 3,代表汉诺塔问题中,从上往下第i个圆盘目前在右
那么arr整体就代表汉诺塔游戏过程中的一个状况
如果这个状况不是汉诺塔最优解运动过程中的状况,返回-1
如果这个状况是汉诺塔最优解运动过程中的状况,返回它是第几个状况(而不是还剩几个状况)
思路
对于传统的汉诺塔问题,如果我要将 123456 从最左边的柱子上移动到最右边的柱子上,需要分成三大步:
- 【第一大步】将 12345 从左边的柱子移动到中间的位置
- 【第二大步】将 6 从左边的柱子移动到右边的位置
- 【第三大步】将 12345 从中间的位置移动到右边的位置
上述传统问题的解法是,定义递归函数 f(i, from, to, other),表示将 [0~i] 的圆盘从 from 柱子移动到 to 柱子上,另外那个柱子叫 other。
对于本题,需要明确一下题意,有几个已知条件:
- 汉诺塔问题,最优解是唯一的路径。
- 题目中给的过程状态,如果不在唯一路径上,就返回-1。
- 举个极端的例子,1层汉诺塔问题,把1从最左边的柱子上移动到最右边的柱子上,只要一步就可以了。而”1在中间这个柱子上“这个状态,就是一个不在最优解路径上的例子。
本题的解法是,定义递归函数int step(int[] arr, int i, int from, int to, int other),表示当前来到 arr 状态下,将 [0~i] 的圆盘从 from 柱子移动到 to 柱子上,另外那个柱子叫 other,返回至少需要几步。
public static int kth(int[] arr) {
int N = arr.length;
return step(arr, N - 1, 1, 3, 2);
}
// 我的疑问:arr为什么全程不更新?
// 自问自答:因为返回它当前走到了第几个状况,而不是还剩几个状况。
public static int step(int[] arr, int index, int from, int to, int other) {
if (index == -1) {
return 0;
}
if (arr[index] == other) { // 最大的数字只可能在from或者to的底部,不可能在other上
return -1;
}
// arr[index]的值,剩下两种情况:
// 情况1:arr[index] == from
// 情况2:arr[index] == to
if (arr[index] == from) { // 情况1:如果index号圆盘还在from上,说明上述连【第一大步】都没走完
// 因为我只想知道当前已经走过多少步了,所以只要统计在【第一大步】中走了多少步就可以了,后面的【第二大步】【第三大步】肯定根本没走
// 怎么统计呢?我们知道【第一大步】的目标是将[0~i-1]从from挪到other上,而且当前已经走到arr状态了,所以就这样继续递归
return step(arr, index - 1, from, other, to);
} else { // 情况2:如果index号圆盘已经在to上了,说明已经完成[0~index-1]的汉诺塔问题了
// 【第一大步】已经完成的从[0~index-1]范围上的index层汉诺塔问题需要的步骤数(n层汉诺塔,最优解2^n-1步)
int p1 = (1 << index) - 1;
// 【第二大步】已经将index号圆盘从from挪到to了,因为我们从arr中看到index号圆盘已经在to上了
int p2 = 1;
// 【第三大步】当前正在经历的,将[0~i-1]号圆盘从other挪到to上,在arr状态下,统计已经走过多少步了?
int p3 = step(arr, index - 1, other, to, from);
// 如果发现它的子问题根本就不是最优解的某一步,直接返回-1
if (p3 == -1) {
return -1;
}
return p1 + p2 + p3;
}
}

题目2:两个岛屿的距离,“感染”问题
Leetcode 原题:
https://leetcode.com/problems/shortest-bridge/
我在力扣上的自己写的答案:
class Solution {
int m, n;
public static final int offset = 100;
public int shortestBridge(int[][] grid) {
m = grid.length;
n = grid[0].length;
// 将其中一个岛A加offset,用来区分两个岛
label:
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (grid[i][j] == 1) {
incr(grid, i, j);
break label; // 中断所有循环,回到label处,但并不重新进入循环
}
}
}
// 左上角主动感染,右下角原地不动
int term = offset;
while (true) {
boolean[][] seen = new boolean[m][n];
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (grid[i][j] == term && !seen[i][j]) {
int result = process(grid, i, j, term, seen);
if (result != Integer.MAX_VALUE) return result - offset;
}
}
}
term++;
}
}
// 当前岛屿向外感染
public int process(int[][] grid, int i, int j, int term, boolean[][] seen) {
int result = Integer.MAX_VALUE;
if (i < 0 || i == m || j < 0 || j == n || seen[i][j]) return result; // 越界,或重复路线
seen[i][j] = true;
if (grid[i][j] == 0) { // 当前位置未感染,则感染
grid[i][j] = term + 1;
} else if (grid[i][j] == term) { // 当前位置是感染源,则去感染周围
result = Math.min(result, process(grid, i + 1, j, term, seen));
result = Math.min(result, process(grid, i - 1, j, term, seen));
result = Math.min(result, process(grid, i, j + 1, term, seen));
result = Math.min(result, process(grid, i, j - 1, term, seen));
} else if (grid[i][j] == 1) { // 两岛接壤,则快速返回
return term;
}
return result;
}
// 给其中一个岛加offset
public void incr(int[][] grid, int i, int j) {
if (i < 0 || i == m || j < 0 || j == n) return;
if (grid[i][j] == 1) {
grid[i][j] = offset;
incr(grid, i + 1, j);
incr(grid, i - 1, j);
incr(grid, i, j + 1);
incr(grid, i, j - 1);
}
}
}
题目3:最大路径和
牛客网原题:
https://www.nowcoder.com/questionTerminal/8ecfe02124674e908b2aae65aad4efdf
给定一个矩阵matrix,先从左上角开始,每一步只能往右或者往下走,走到右下角。然后从右下角出发,每一步只能往上或者往左走,再回到左上角。任何一个位置的数字,只能获得一遍。返回最大路径和。
输入描述
第一行输入两个整数M和N,M,N<=200
接下来M行,每行N个整数,表示矩阵中元素
5 10
1 1 1 1 1 0 0 0 0 0
0 0 0 0 1 0 0 0 0 0
0 0 0 0 1 0 0 0 0 1
1 0 0 0 1 0 0 0 0 0
0 0 0 0 1 1 1 1 1 1
输出描述
输出一个整数,表示最大路径和
16
思路
第一次见到这题,是在体系学习班第14节。当时只讲了不能贪心,应该用dp,但没有细说。
黄色部分表示我想要拿到的位置:
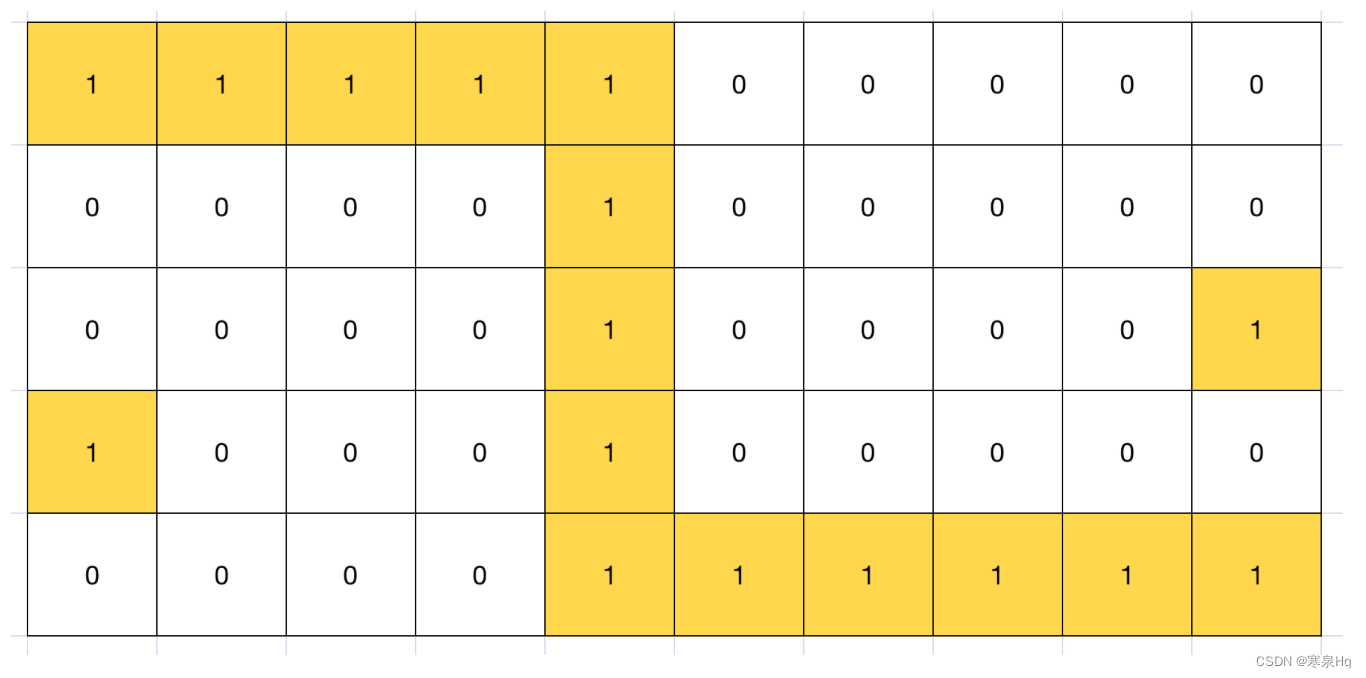
错误的贪心路径
少拿一个灰色的格子。

正确的路径
最好情况下,能够拿到所有的格子。

虽然题目要求是一来一回,但我们可以想象成有两个人 a、b,都从左上角走到右下角,求整个过程中,最多能拿到多少值。
内存超限版本如下。其实可以省掉一个维度就不会超了,因为(i1, j1), (i2, j2) 两个坐标中,存在关系:i1+j1=i2+j2。可变参数数量能省则省!
import java.util.Scanner;
// 注意类名必须为 Main, 不要有任何 package xxx 信息
public class Main {
static int[][] arr;
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int m = in.nextInt();
int n = in.nextInt();
arr = new int[m][n];
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
arr[i][j] = in.nextInt();
}
}
int[][][][] dp = new int[m][n][m][n];
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
for (int k = 0; k < m; k++) {
for (int l = 0; l < n; l++) {
dp[i][j][k][l] = -1;
}
}
}
}
int res = process(0, 0, 0, 0, dp);
System.out.println(res);
}
// 当前a在i1,j1位置,b在i2,j2位置
// 两个人都只能向右走或者向下走,求能拿到的最多点数
public static int process(int i1, int j1, int i2, int j2, int[][][][] dp) {
if (i1 == arr.length || j1 == arr[0].length) return 0;
if (i2 == arr.length || j2 == arr[0].length) return 0;
if (dp[i1][j1][i2][j2] >= 0) return dp[i1][j1][i2][j2];
// a,b如果走到了同一个位置,点数只能累加一次
int res = arr[i1][j1];
if (i1 != i2 && j1 != j2) res += arr[i2][j2];
// a向右,b向右
int p1 = process(i1 + 1, j1, i2 + 1, j2, dp);
// a向下,b向下
int p2 = process(i1, j1 + 1, i2, j2 + 1, dp);
// a向右,b向下
int p3 = process(i1, j1 + 1, i2 + 1, j2, dp);
// a向下,b向右
int p4 = process(i1 + 1, j1, i2, j2 + 1, dp);
res += Math.max(Math.max(p1, p2), Math.max(p3, p4));
dp[i1][j1][i2][j2] = res;
return res;
}
}
/*
5 10
1 1 1 1 1 0 0 0 0 0
0 0 0 0 1 0 0 0 0 0
0 0 0 0 1 0 0 0 0 1
1 0 0 0 1 0 0 0 0 0
0 0 0 0 1 1 1 1 1 1
2 2
1 1
1 1
*/
题目4
牛客网原题:
https://www.nowcoder.com/practice/7201cacf73e7495aa5f88b223bbbf6d1
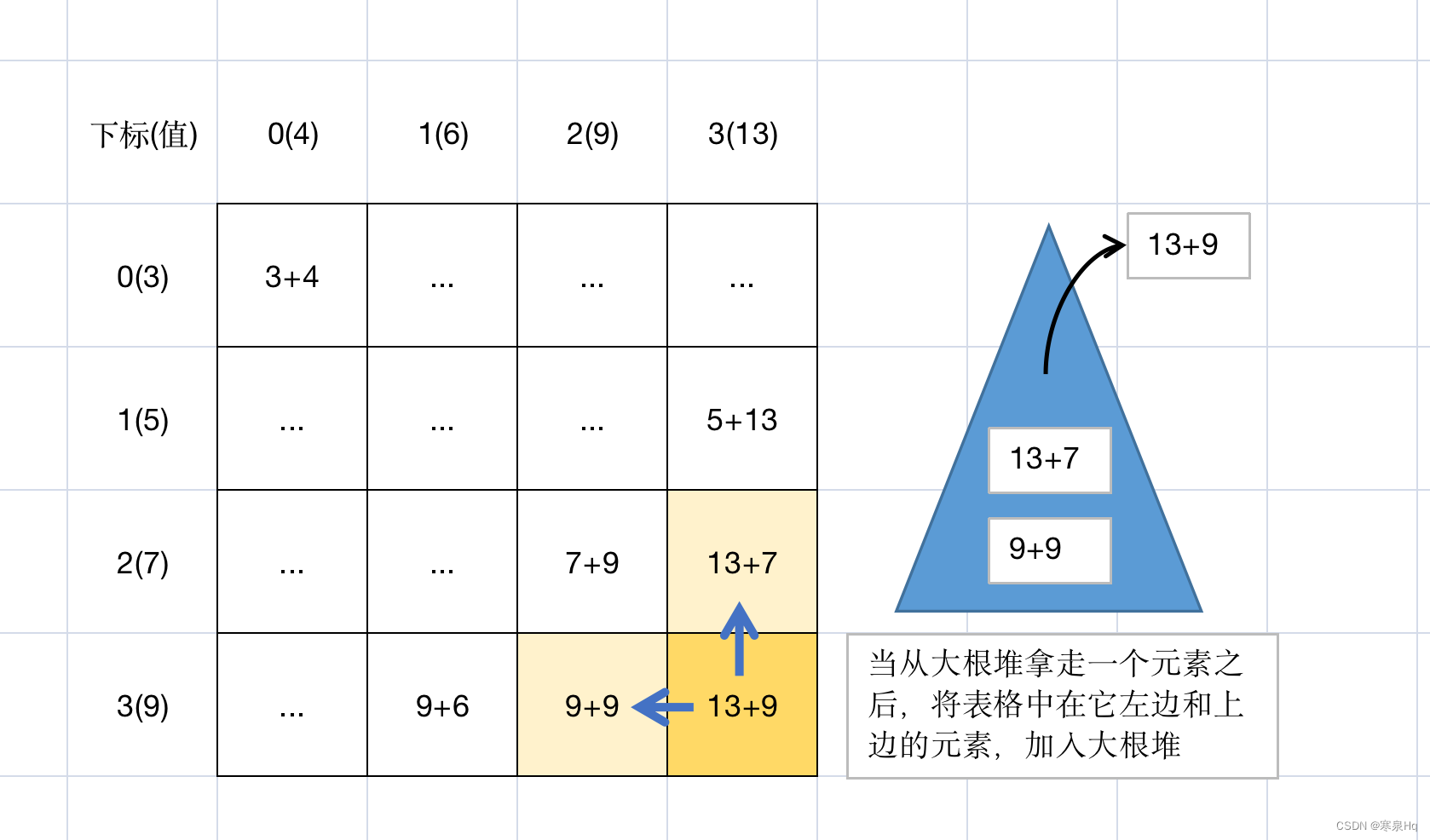
给定两个有序数组arr1和arr2,再给定一个整数k,你可以从来自arr1和arr2的两个数各选一个数,返回相加和最大的前k个。
思路
不能用双指针从最右边开始往左滑动,因为这样会丢失本来可以重复使用的数字。
正确的方法是用大根堆。
当从大根堆拿走一个元素之后,将表格中在它左边和上边的元素,加入大根堆。