因果推断(四)断点回归(RD)
在传统的因果推断方法中,有一种方法可以控制观察到的混杂因素和未观察到的混杂因素,这就是断点回归,因为它只需要观察干预两侧的数据,是否存在明显的断点。
⚠️注意:当然这个方法只能做到局部随机,因此很难依据该结论推向全局。
本文参考自rdd官方示例,通过python的rdd包展示如何进行断点回归分析。
准备数据
# pip install rdd
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from rdd import rdd
# 设置随机种子
np.random.seed(42)
# 构造数据
N = 10000
x = np.random.normal(1, 1, N)
epsilon = np.random.normal(0, 1, N)
threshold = 1
treatment = np.where(x >= threshold, 1, 0)
w1 = np.random.normal(0, 1, N) # 控制变量1
w2 = np.random.normal(0, 4, N) # 控制变量2
y = .5 * treatment + 2 * x - .2 * w1 + 1 + epsilon
data = pd.DataFrame({'y':y, 'x': x, 'w1':w1, 'w2':w2})
data.head()
| y | x | w1 | w2 | |
|---|---|---|---|---|
| 0 | 3.745276 | 1.496714 | 0.348286 | -7.922288 |
| 1 | 2.361307 | 0.861736 | 0.283324 | -4.219943 |
| 2 | 4.385300 | 1.647689 | -0.936520 | -2.348114 |
| 3 | 6.540561 | 2.523030 | 0.579584 | 0.598676 |
| 4 | 4.026888 | 0.765847 | -1.490083 | 4.096649 |
模型拟合
# 设置带宽,只观察断点附近的数据表现
bandwidth_opt = rdd.optimal_bandwidth(data['y'], data['x'], cut=threshold)
print("Optimal bandwidth:", bandwidth_opt)
# 筛选带宽内数据
data_rdd = rdd.truncated_data(data, 'x', bandwidth_opt, cut=threshold)
Optimal bandwidth: 0.7448859965965812
结果展示
# 查看效果
plt.figure(figsize=(12, 8))
plt.scatter(data_rdd['x'], data_rdd['y'], facecolors='none', edgecolors='r')
plt.xlabel('x')
plt.ylabel('y')
plt.axvline(x=threshold, color='b')
plt.show()
plt.close()
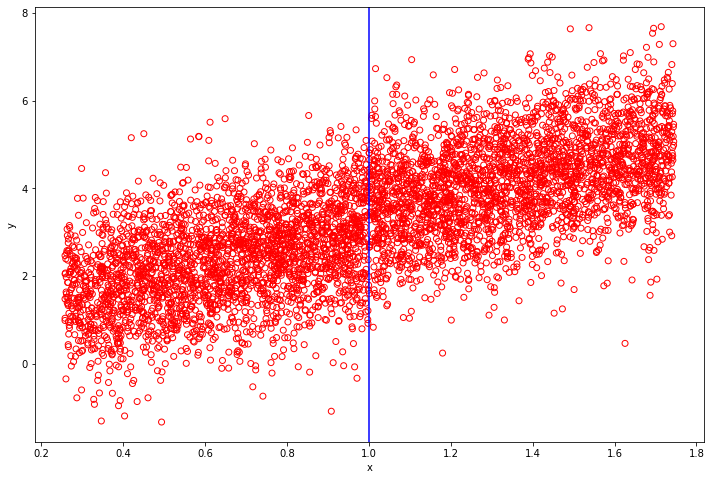
# 数据混杂较多的噪音,对数据进行分箱,减少噪音
data_binned = rdd.bin_data(data_rdd, 'y', 'x', 100)
plt.figure(figsize=(12, 8))
plt.scatter(data_binned['x'], data_binned['y'],
s = data_binned['n_obs'], facecolors='none', edgecolors='r')
plt.axvline(x=threshold, color='b')
plt.xlabel('x')
plt.ylabel('y')
plt.show()
plt.close()

模型评估
# 查看模型效果
print('\n','{:*^80}'.format('model summary:'),'\n')
model = rdd.rdd(data_rdd, 'x', 'y', cut=threshold)
print(model.fit().summary())
# 手动增加协变量,更改协方差类型
print('\n','{:*^80}'.format('model summary customize 1:'),'\n')
model = rdd.rdd(data_rdd, 'x', 'y', cut=threshold, controls=['w1', 'w2'])
print(model.fit(cov_type='hc1').summary())
# 手动设置拟合方程
print('\n','{:*^80}'.format('model summary customize 2:'),'\n')
model = rdd.rdd(data_rdd, 'x', cut=threshold, equation='y ~ TREATED + x + w1*w2')
print(model.fit().summary())
*********************************model summary:*********************************
Estimation Equation: y ~ TREATED + x
WLS Regression Results
==============================================================================
Dep. Variable: y R-squared: 0.508
Model: WLS Adj. R-squared: 0.508
Method: Least Squares F-statistic: 2811.
Date: Sun, 02 Oct 2022 Prob (F-statistic): 0.00
Time: 00:53:56 Log-Likelihood: -7794.0
No. Observations: 5442 AIC: 1.559e+04
Df Residuals: 5439 BIC: 1.561e+04
Df Model: 2
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
Intercept 1.0297 0.046 22.267 0.000 0.939 1.120
TREATED 0.4629 0.054 8.636 0.000 0.358 0.568
x 1.9944 0.065 30.776 0.000 1.867 2.121
==============================================================================
Omnibus: 2.452 Durbin-Watson: 2.036
Prob(Omnibus): 0.293 Jarque-Bera (JB): 2.429
Skew: -0.034 Prob(JB): 0.297
Kurtosis: 3.077 Cond. No. 10.3
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
***************************model summary customize 1:***************************
Estimation Equation: y ~ TREATED + x + w1 + w2
WLS Regression Results
==============================================================================
Dep. Variable: y R-squared: 0.523
Model: WLS Adj. R-squared: 0.523
Method: Least Squares F-statistic: 1520.
Date: Sun, 02 Oct 2022 Prob (F-statistic): 0.00
Time: 00:53:56 Log-Likelihood: -7709.9
No. Observations: 5442 AIC: 1.543e+04
Df Residuals: 5437 BIC: 1.546e+04
Df Model: 4
Covariance Type: hc1
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
Intercept 1.0297 0.045 22.797 0.000 0.941 1.118
TREATED 0.4783 0.054 8.870 0.000 0.373 0.584
x 1.9835 0.064 30.800 0.000 1.857 2.110
w1 -0.1748 0.014 -12.848 0.000 -0.201 -0.148
w2 0.0081 0.003 2.372 0.018 0.001 0.015
==============================================================================
Omnibus: 2.687 Durbin-Watson: 2.031
Prob(Omnibus): 0.261 Jarque-Bera (JB): 2.692
Skew: -0.032 Prob(JB): 0.260
Kurtosis: 3.088 Cond. No. 26.3
==============================================================================
Notes:
[1] Standard Errors are heteroscedasticity robust (HC1)
***************************model summary customize 2:***************************
Estimation Equation: y ~ TREATED + x + w1*w2
WLS Regression Results
==============================================================================
Dep. Variable: y R-squared: 0.523
Model: WLS Adj. R-squared: 0.523
Method: Least Squares F-statistic: 1194.
Date: Sun, 02 Oct 2022 Prob (F-statistic): 0.00
Time: 00:53:56 Log-Likelihood: -7709.6
No. Observations: 5442 AIC: 1.543e+04
Df Residuals: 5436 BIC: 1.547e+04
Df Model: 5
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
Intercept 1.0303 0.046 22.617 0.000 0.941 1.120
TREATED 0.4784 0.053 9.054 0.000 0.375 0.582
x 1.9828 0.064 31.054 0.000 1.858 2.108
w1 -0.1746 0.014 -12.831 0.000 -0.201 -0.148
w2 0.0080 0.003 2.362 0.018 0.001 0.015
w1:w2 -0.0025 0.003 -0.737 0.461 -0.009 0.004
==============================================================================
Omnibus: 2.725 Durbin-Watson: 2.031
Prob(Omnibus): 0.256 Jarque-Bera (JB): 2.732
Skew: -0.033 Prob(JB): 0.255
Kurtosis: 3.088 Cond. No. 26.9
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
上述模型表明TREATED有显著影响
模型验证
# 模型验证
data_placebo = rdd.truncated_data(data, 'x', yname='y', cut=0) # 任意位置设置断点
# 查看验证效果
model = rdd.rdd(data_placebo, 'x', 'y', cut=0, controls=['w1'])
print(model.fit().summary())
Estimation Equation: y ~ TREATED + x + w1
WLS Regression Results
==============================================================================
Dep. Variable: y R-squared: 0.375
Model: WLS Adj. R-squared: 0.374
Method: Least Squares F-statistic: 660.8
Date: Sun, 02 Oct 2022 Prob (F-statistic): 0.00
Time: 00:53:56 Log-Likelihood: -4633.4
No. Observations: 3310 AIC: 9275.
Df Residuals: 3306 BIC: 9299.
Df Model: 3
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
Intercept 1.0154 0.039 26.118 0.000 0.939 1.092
TREATED 0.0294 0.068 0.433 0.665 -0.104 0.163
x 1.9780 0.087 22.631 0.000 1.807 2.149
w1 -0.1752 0.017 -10.245 0.000 -0.209 -0.142
==============================================================================
Omnibus: 3.151 Durbin-Watson: 2.006
Prob(Omnibus): 0.207 Jarque-Bera (JB): 3.114
Skew: 0.057 Prob(JB): 0.211
Kurtosis: 3.098 Cond. No. 8.15
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
随机设置断点在位置0,TREATED影响不显著符合预期
总结
RDD能很好的针对政策干预、营销活动的影响效果进行因果推断。例如某平台粉丝数达到10w会呈现大【V】标,我们就可以利用断点回归查看小于10万附近的用户收益和高于10万用户附近的用户收益,是否存在明显的断点。
共勉~