Tree相关

1.树相关题目

1.1 二叉树的中序遍历（简单）：递归

题目：使用中序遍历二叉树

思想：按照访问左子树——根节点——右子树的方式遍历这棵树，而在访问左子树或者右子树的时候我们按照同样的方式遍历，直到遍历完整棵树

总结：对于一棵树而言，从根节点出发，有左子树和右子树；而对于左子树和右子树而言，根节点下的第一个左子树节点可以看作一个新的根节点，依次类推，因此在树种大部分会使用到递归这个概念

代码：定义 inorder(root) 表示当前遍历到 root 节点的答案

public class TreeNode{
    int val;
    TreeNode left;
    TreeNode right;
    TreeNode(){
        
    }
    TreeNode(int val){
        this.val = val;
    }
    TreeNode(int val,TreeNode tight,TreeNode left){
        this.val = val;
        this.left = left;
        this.right = right;  
    }
}

class Solution{
    public List<Integer> inorderTraversal(TreeNode root){
        List<Integer> list = new ArrayList<>();
        inorder(root,list);
        return list;
    }
    
    public void inorder(TreeNode root,List<Integer> list){
        if(root == null){
            return;
        }
        //遍历左子树
        inorder(root.left,list);
        //加入中间节点
        list.add(root.val);
        //遍历右子树
        inorder(root.right,list);
    }
}

1.2 不同的二叉搜索树Ⅰ（中等）：动态规划

题目：给一个节点，求出有多少种不同的二叉搜索树

思想：因此在生成所有可行的二叉搜索树的时候，假设当前序列长度为 n，如果我们枚举根节点的值为 i，那么根据二叉搜索树的性质我们可以知道左子树的节点值的集合为 1…i−1[1…i−1]，右子树的节点值的集合为 i+1…n[i+1…n]。使用动态规划来求解本题；则根为 i 的所有二叉搜索树的集合是左子树集合和右子树集合的笛卡尔积，对于笛卡尔积中的每个元素，加上根节点之后形成完整的二叉搜索树

笛卡尔积：笛卡尔积是一种数学运算，它将两个集合的元素分别组合起来，生成一个新的集合。新集合中的每个元素都是由两个集合中的一个元素组成的有序对，其中第一个元素来自第一个集合，第二个元素来自第二个集合。简单来说，就是将两个集合中的元素进行组合，生成所有可能的组合情况。

例如，有两个集合A={1,2}和B={a,b}，它们的笛卡尔积为{(1,a),(1,b),(2,a),(2,b)}。其中，第一个元素为1或2，第二个元素为a或b，共有4种组合情况。

总结：对于一组任意序列而言，能够产生的二叉搜索树是很多的；根据二叉搜索树的定义约束，我们可以任意选用根节点，然后选择根节点的左边和右边序列组成所有可能的左子树和右子树，最终连接即可；公式为：

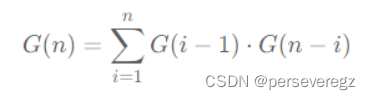
代码：

class Solution {
    public int numTrees(int n) {
        //G为n+1是为了存G[0]
        int[] G = new int[n+1];
        G[0] = 1;
        G[1] = 1;

        //由于G[n] = Σ(G[i -1]*G[n-i]);
        //将i当作n，对应求和中的上限n
        for(int i =2 ; i <= n; ++i){
            //将j当作i。对应求和中的遍历i
            for(int j = 1; j <= i ; ++j){
                G[i] += G[j - 1] * G[i - j]; 
            }
        }
        return G[n];
    }
}

1.3 不同的二叉搜索树Ⅱ（中等）：回溯

题目：给一个节点，将这个节点有多少种二叉搜索树全部展示出来

思想：二叉搜索树BST的性质为：根节点的值大于左子树所有节点的值，小于右子树所有节点的值，且左子树和右子树也同样为二叉搜索树；因此在生成所有可行的二叉搜索树的时候，假设当前序列长度为 n，如果我们枚举根节点的值为 i，那么根据二叉搜索树的性质我们可以知道左子树的节点值的集合为 1…i−1[1…i−1]，右子树的节点值的集合为 i+1…n[i+1…n]。而左子树和右子树的生成相较于原问题是一个序列长度缩小的子问题；采用回溯的方法来解决这道题目

总结：与第一题类似，我们展示所有的二叉搜索树也可以选用不同的根节点，将根节点两边序列分别递归得到左右子树，组合为一个树即可

代码：

public class TreeNode{
    int val;
    TreeNode left;
    TreeNode right;
    TreeNode(){
        
    }
    TreeNode(int val){
        this.val = val;
    }
    TreeNode(int val,TreeNode tight,TreeNode left){
        this.val = val;
        this.left = left;
        this.right = right;  
    }
}

class Solution {
    public List<TreeNode> generateTrees(int n) {
        if (n == 0) {
            return new LinkedList<TreeNode>();
        }
        return generateTrees(1, n);
    }

    public List<TreeNode> generateTrees(int start, int end) {
        List<TreeNode> allTrees = new LinkedList<TreeNode>();
        if (start > end) {
            allTrees.add(null);
            return allTrees;
        }

        // 枚举可行根节点；每一个都可以做根节点
        for (int i = start; i <= end; i++) {
            
            //用相同的方法做两次相同的行为
            
            // 获得所有可行的左子树集合
            List<TreeNode> leftTrees = generateTrees(start, i - 1);

            // 获得所有可行的右子树集合
            List<TreeNode> rightTrees = generateTrees(i + 1, end);

            //将可行的左子树、右子树、根节点组合
            // 从左子树集合中选出一棵左子树，从右子树集合中选出一棵右子树，拼接到根节点上
            for (TreeNode left : leftTrees) {
                for (TreeNode right : rightTrees) {
                    TreeNode currTree = new TreeNode(i);
                    currTree.left = left;
                    currTree.right = right;
                    allTrees.add(currTree);
                }
            }
        }
        return allTrees;
    }
}

1.4 验证二叉搜索树（中等）

题目：给一个二叉树的根节点，判断是否是有效的二叉搜索树

思想：如果该二叉树的左子树不为空，则左子树上所有节点的值均小于它的根节点的值；若它的右子树不空，则右子树上所有节点的值均大于它的根节点的值；它的左右子树也为二叉搜索树

总结：二叉搜索树的性质是左边子树值均小于根节点，右边子树值均大于根节点，且其左右子树也满足该性质，左右子树的判断进行递归即可；此题的思想一样是：利用根节点的左右两端小于/大于的情况，生成判断isValidBST(root,Long.MIN_VALUE,Long.MAX_VALUE)

代码：什么是递归？就是大的用的方法，小的也用到了，那就一起用

class Solution {
    public boolean isValidBST(TreeNode root) {
        return isValidBST(root,Long.MIN_VALUE,Long.MAX_VALUE);
    }

    public boolean isValidBST(TreeNode root,long lower,long upper){
        if(root == null){
            return true;
        }
        if(root.val <= lower || root.val >= upper){
            return false;
        }

        //对于root的左节点而言，都小于根节点；对于root的右节点而言，都大于根节点
        return isValidBST(root.left,lower,root.val) && isValidBST(root.right,root.val,upper);
    }
}

1.5 二叉树的层序遍历（中等）：广度优先搜索+队列

题目：给你二叉树的根节点 root ，返回其节点值的 层序遍历 。（即逐层地，从左到右访问所有节点）

思想：创建一个队列，从根节点开始入队出队，然后是左右子节点入队出队；如果队列不为空：若队列长度为s，则遍历s输出即可

总结：使用队列的方式：先将根节点入队，然后让左右子节点以此入队出队即可；先判断队列是否为空，然后根据队列长度输出元素

代码：

class Solution {
    public List<List<Integer>> levelOrder(TreeNode root) {
        
        List<List<Integer>> res = new ArrayList<>();
        
        if(root == null){
            return res;
        }
        
        //创建一个队列
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);

        //判断是否为空
        while(!queue.isEmpty()){
            List<Integer> list = new ArrayList<>();
            int len = queue.size();
            
            //根据长度出队
            for(int i = 1; i <= len; ++i){
                TreeNode currRoot = queue.poll();
                if(currRoot.left != null){
                    queue.offer(currRoot.left);
                }
                if(currRoot.right != null){
                    queue.offer(currRoot.right);
                }
                list.add(currRoot.val);
            }
            res.add(list);
        }
        return res;
    }
}

1.6 相同的树（简单）：深度优先搜索+递归

题目：给你两棵二叉树的根节点 p 和 q ，编写一个函数来检验这两棵树是否相同

思想：

判断是否为空
- 如果两个二叉树都为空，则两个二叉树相同
- 如果两个二叉树中有且只有一个为空，则两个二叉树一定不相同。
如果两个二叉树都不为空，判断根节点与左右子树
- 那么首先判断它们的根节点的值是否相同，若不相同则两个二叉树一定不同，
- 若相同，再分别判断两个二叉树的左子树是否相同以及右子树是否相同
- 这是一个递归的过程，因此可以使用深度优先搜索，递归地判断两个二叉树是否相同

总结：判断树是否相同：利用深度优先搜索；判断是否都为空、根节点是否相同、子树是否相同

代码：什么是递归？就是大的用的方法，小的也用到了，那就一起用

什么是深度优先搜索？从上往下依次搜索

lass Solution {
    public boolean isSameTree(TreeNode p, TreeNode q) {
        //是否为空
        if(p == null && q == null){
            return true;
        }//是否只有一个为空
        else if(p == null || q == null){
            return false;
        }//根节点是否相同
        else if(p.val != q.val){
            return false;
        }//左右子树是否相同
        else{
            return isSameTree(p.left,q.left) && isSameTree(p.right,q.right);
        }
    }
}

1.7 从前序与中序遍历序列构造二叉树（中等）：递归

题目：给定两个整数数组 preorder 和 inorder ，其中 preorder 是二叉树的前序遍历， inorder 是同一棵树的中序遍历，请构造二叉树并返回其根节点。

思想：只要我们在中序遍历中定位到根节点，那么我们就可以分别知道左子树和右子树中的节点数目。由于同一颗子树的前序遍历和中序遍历的长度显然是相同的，因此我们就可以对应到前序遍历的结果中，对上述形式中的所有左右括号进行定位

总结：前序遍历和中序遍历都给出了所有树节点；前序第一个节点就是根节点，将其找到，在中序遍历中就能得到根节点的左右子树节点的个数，然后根据其个数将其递归组合为一个二叉树即可

代码：

class Solution {
    
    private Map<Integer, Integer> indexMap;

    public TreeNode buildTree(int[] preorder, int[] inorder) {
        int n = preorder.length;
        // 构造哈希映射，帮助我们快速定位根节点
        indexMap = new HashMap<Integer, Integer>();
        for (int i = 0; i < n; i++) {
            indexMap.put(inorder[i], i);
        }
        return myBuildTree(preorder, inorder, 0, n - 1, 0, n - 1);
    }
    
    
    public TreeNode myBuildTree(int[] preorder, int[] inorder, int preorder_left, int preorder_right, int inorder_left, int inorder_right) {
        if (preorder_left > preorder_right) {
            return null;
        }

        // 前序遍历中的第一个节点就是根节点
        int preorder_root = preorder_left;
        // 在中序遍历中定位根节点
        int inorder_root = indexMap.get(preorder[preorder_root]);
        
        // 先把根节点建立出来
        TreeNode root = new TreeNode(preorder[preorder_root]);
        // 得到左子树中的节点数目
        int size_left_subtree = inorder_root - inorder_left;
        // 递归地构造左子树，并连接到根节点
        //先序遍历中「从 左边界+1 开始的 size_left_subtree」个元素就对应了中序遍历中「从 左边界 开始到 根节点定位-1」的元素
        root.left = myBuildTree(preorder, inorder, preorder_left + 1, preorder_left + size_left_subtree, inorder_left, inorder_root - 1);
        // 递归地构造右子树，并连接到根节点
        // 先序遍历中「从 左边界+1+左子树节点数目 开始到 右边界」的元素就对应了中序遍历中「从 根节点定位+1 到 右边界」的元素
        root.right = myBuildTree(preorder, inorder, preorder_left + size_left_subtree + 1, preorder_right, inorder_root + 1, inorder_right);
        return root;
    }
}

1.8 平衡二叉树（简单）：自顶向下+递归

题目：给定一个二叉树，判断它是否是高度平衡的二叉树；

高度平衡：一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1
二叉树的高度：其左右子树的最大高度+1

思想：一棵二叉树是平衡二叉树，当且仅当其所有子树也都是平衡二叉树，因此可以使用递归的方式判断二叉树是不是平衡二叉树，递归的顺序可以是自顶向下或者自底向上

总结：在做树的题时，都要先将root == null的情况一判断；然后根据题目去求解；比如平衡二叉树按照定义来做：左右子树高度差小于等于1，左右子树也都为平衡二叉树；节点高度是左右子树最大高度 + 1

代码：

class Solution {
    public boolean isBalanced(TreeNode root) {
        if(root == null){
            return true;
        }
        //平衡二叉树：
        //左右子树高度差 <= 1 且 左右子树也均为平衡二叉树
        return Math.abs(height(root.left) - height(root.right)) <= 1 && isBalanced(root.left) && isBalanced(root.right);
    }

    public int height(TreeNode root){
        if(root == null){
            return 0;
        }
        //二叉树的高度为：左右子树最大高度 + 1
        return Math.max(height(root.left),height(root.right)) + 1;
    }
}

1.9 二叉树的最小深度（简单）：深度优先搜索/广度优先搜索 + 递归

题目：给定一个二叉树，找出其最小深度；最小深度是从根节点到最近叶子节点的最短路径上的节点数量

思想：深度优先搜索：

如果根节点为空，返回0
- 如果只有根节点，返回1
  - 如果有左右子树，则最小深度就是左右子树的最小深度 + 1

总结：深度优先搜索可以将问题拆分为小问题，然后利用递归来解决

代码：

class Solution {
    public int minDepth(TreeNode root) {
        //如果没有根节点，返回0
        if(root == null){
            return 0;
        }

        //如果只有根节点，返回1
        if(root.left == null && root.right == null){
            return 1;
        }

        int min_Depth = Integer.MAX_VALUE;
        //如果有子树：分别比较左右子树深度哪个更小，然后将其加1并返回
        if(root.left != null){
            min_Depth = Math.min(minDepth(root.left),min_Depth);
        }
        if(root.right != null){
            min_Depth = Math.min(minDepth(root.right),min_Depth);
        }

        return min_Depth + 1;
    }
}

1.10 二叉树展开为链表（中等）：前序遍历

题目：给你二叉树的根结点 root ，请你将它展开为一个单链表;

展开后的单链表应该同样使用 TreeNode ，其中 right 子指针指向链表中下一个结点，而左子指针始终为 null 。
展开后的单链表应该与二叉树先序遍历顺序相同。

思想：先前序遍历得到单链表的顺序，然后将各节点的左节点指向null，右节点指向下一个前序遍历中的节点

总结：深度优先搜索可以将问题拆分为小问题，然后利用递归来解决

代码：

class Solution {
    public void flatten(TreeNode root) {
        //先拿到前序遍历后的节点(注意此时不是要值，因此可以不用取树的值)，作为单链表展开后的顺序
        List<TreeNode> list = new ArrayList<>();
        preorder(root,list);

        //将单链表左节点设为null，右节点赋为先序遍历的下一个值
        //这里长度为 list.size() - 1,因为倒数第二个节点可以有左右子节点，但倒数第一个节点肯定是没有左右子节点的
        for(int i = 0; i < list.size() - 1; i++){
            TreeNode prev = list.get(i);
            prev.left = null;
            prev.right = list.get(i + 1);
        }
    }

    public void preorder(TreeNode root,List<TreeNode> list){
        if(root == null){
            return;
        }
        list.add(root);
        preorder(root.left,list);
        preorder(root.right,list);
    }
}

1.11 二叉树的最近公共祖先（中等）：递归

题目：给定一个二叉树, 找到该树中两个指定节点的最近公共祖先

最近公共祖先的定义为：“对于有根树 T 的两个节点 p、q，最近公共祖先表示为一个节点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

思想：两种情况：

公共祖先不是自己
公共祖先是自己

因此可以先定义一个函数：fx：表示x节点的子树中是否包含p或者q

总结：首先需要读懂题意，然后才能入手解决这种较为复杂的问题，可以设置一个专门判断是否存在节点p、q的函数，从而根据两种情况递归的使用该函数，最终得到结果

代码：

class Solution {

    //用来保存最近公共祖先
    private TreeNode res;

    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        isSon(root,p,q);
        return this.res;
    }

    //定义一个函数，用来检查root中是否包含p或者q，是则返回true（该方法无法直接找到公共祖先，而是找到包含p或者q的节点）
    public boolean isSon(TreeNode root,TreeNode p,TreeNode q){
        if(root == null){
            return false;
        }
        //root的左子节点包含p或q
        boolean lson = isSon(root.left,p,q);
        //root的右子节点包含p或者q
        boolean rson = isSon(root.right,p,q);
        //如果root的左右子节点各包含了p、q，说明root就是最近公共祖先节点
        if(lson && rson){
            this.res = root;
        }
        //如果root本身就是q或者q，则root就是最近公共祖先
        if((root.val == p.val || root.val == q.val) && (lson || rson)){
            this.res = root;
        }
        //若左子树、右子树、节点本身就包含p或者q，就返回true
        return lson || rson || (root.val == p.val || root.val == q.val);
    }

}

1.12 填充每个节点的下一个右侧节点指针（中等）：层次遍历

题目：给定一个 完美二叉树 ，其所有叶子节点都在同一层，每个父节点都有两个子节点，填充它的每个 next 指针，让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点，则将 next 指针设置为 NULL。

思想：对二叉树进行层次遍历，然后对其节点进行右侧指针连接

总结：只需进行层次遍历，便能够得到每个节点，然后队列出队时，只要不是倒数第一个元素就将队列头部元素赋给出队元素指针即可

代码：

补充：Java中Queue共有6个方法：

1、offer函数和add函数的区别

在一个满的队列中加入一个新项，多出的项就会被拒绝。

add() ：在队列中添加元素；若队列已满抛出 unchecked 异常

offer() :在队列中添加元素；若队列已满返回 false。

2、poll函数和remove函数的区别

remove()：从队列中删除第一个元素；若集合为空返回异常

poll() ：从队列中删除第一个元素；若集合为空返回null

3、peek函数和element函数的区别

element() ：在队列头部查询元素；若集合为空返回异常

peek() ：在队列头部查询元素；若集合为空返回null

class Solution {
    public Node connect(Node root) {
        if(root == null){
            return root;
        }

        //创建队列用来进行层次遍历时的入队出队
        Queue<Node> queue = new LinkedList<>();
        queue.add(root);

        //循环：先判断queue是否为空，不为空则遍历queue所有元素出队操作
        while(!queue.isEmpty()){
            int len = queue.size();
            for(int i = 0; i < len; i++){

                Node node = queue.poll();

                //在层序遍历中加入：连接右侧指针操作
                if(i < len - 1){
                    //查询此时queue中的头部元素，将其赋给node指针next
                    node.next = queue.peek();
                }

                if(node.left != null){
                    queue.add(node.left);
                }
                if(node.right != null){
                    queue.add(node.right);
                }
            }
        }
        return root;
    }
}

1.13 二叉树的右视图（中等）：深度优先搜索/广度优先搜索

题目：给定一个二叉树的 根节点 root，想象自己站在它的右侧，按照从顶部到底部的顺序，返回从右侧所能看到的节点值

思想：对树进行深度优先搜索，搜索过程中，先访问右子树，则第一个节点就是最右边的节点；知道树的层数，就能得到最终的结果数组

总结：要注意当右侧没有节点时，左子树节点的值也是右侧视图能够看到的节点

代码：

class Solution {
    public List<Integer> rightSideView(TreeNode root) {
        //创建存入右侧节点的数组
        List<Integer> res = new ArrayList<>();
        dfs(res, root, 0);
        return res;
    }

    public void dfs(List<Integer> res, TreeNode root, int level){
        if(root != null){
            //只有在当前深度才能加入节点值
            if(res.size() == level){
                res.add(root.val);
            }
            //右视图，则先遍历右边节点，然后将其插入数组
            dfs(res, root.right, level + 1);
            //如果没有右节点，那么左节点就是右侧视图的第一个节点
            dfs(res, root.left, level + 1);
        }
    }
}