1.模型原理

模型原理：

朴素贝叶斯分类是基于贝叶斯定理的一种分类方法。它假设特征之间相互独立（朴素性），从而简化计算过程。朴素贝叶斯分类器适用于文本分类、垃圾邮件过滤、情感分析等多种应用场景。

贝叶斯定理：

在朴素贝叶斯分类中，我们使用贝叶斯定理来计算后验概率。对于一个待分类的数据点，假设其特征向量为 $\mathbf{x}$，类别为 $y$，贝叶斯定理表示为：

$$P(y|\mathbf{x})=\frac{P(\mathbf{x}|y)\cdot P(y)}{P(\mathbf{x})}$$

其中，

• $P(y|\mathbf{x})$：给定特征 $\mathbf{x}$ 的情况下，类别 $y$ 的后验概率。
• $P(\mathbf{x}|y)$：在类别 $y$ 下，特征 $\mathbf{x}$ 的条件概率。
• $P(y)$：类别 $y$ 的先验概率。
• $P(\mathbf{x})$：特征 $\mathbf{x}$ 的边缘概率。

朴素性假设：

朴素贝叶斯分类器假设特征之间相互独立，即给定类别的情况下，特征之间没有关联。这个假设大大简化了计算过程，尽管在实际情况中很少有特征完全独立的情况。尽管如此，朴素贝叶斯分类器在实际应用中表现良好。

数学模型：

在朴素贝叶斯分类中，我们需要计算条件概率，主要有两种类型：离散型特征和连续型特征。

离散型特征：

对于离散型特征，我们可以计算每个特征值在给定类别下的条件概率：

$$P(x_i|y)=\frac{\text{Count}(x_i,y)+1}{\text{Count}(y)+|X_i|}$$

其中，

• $\text{Count}(x_i,y)$：在类别 $y$ 下，特征 $x_i$ 出现的次数。
• $\text{Count}(y)$：类别 $y$ 的样本总数。
• $|X_i|$：特征 $x_i$ 可能的取值数量。

连续型特征：

对于连续型特征，我们通常假设特征的分布是高斯分布（正态分布），然后计算每个特征在给定类别下的均值和方差，然后使用高斯分布的概率密度函数计算条件概率：

$$P(x_i|y)=\frac{1}{\sqrt{2\pi }\cdot {\sigma }_y}\cdot \exp \left(-\frac{(x_i-{\mu }_y{)}^2}{2{\sigma }_y^2}\right)$$

其中，

• ${\mu }_y$：在类别 $y$ 下，特征 $x_i$ 的均值。
• ${\sigma }_y$：在类别 $y$ 下，特征 $x_i$ 的标准差。

朴素贝叶斯分类器通过计算每个类别的后验概率来进行分类决策，选择具有最大后验概率的类别作为预测结果。虽然朴素贝叶斯分类器假设特征之间相互独立，在实际应用中仍然表现良好，并且具有较快的训练和预测速度。

2.模型参数

GaussianNB类是朴素贝叶斯分类器的一种实现，用于处理连续型特征。以下是GaussianNB类的主要参数列表：

1. priors: 先验概率，可以为None（默认）或array-like。如果为None，使用数据中的样本数来估计先验概率；如果为array-like，则指定每个类别的先验概率。

2. var_smoothing: 方差平滑项，一个非负数。默认为1e-9。用于稳定计算，避免概率为零的情况。

3.文件结构

iris.xlsx						% 可替换数据集
Main.py							% 主函数

4.Excel数据

5.下载地址

- 资源下载地址

6.完整代码

import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.naive_bayes import GaussianNB
from sklearn.metrics import accuracy_score, confusion_matrix
import matplotlib.pyplot as plt
import seaborn as sns

def naive_bayes_classification(data_path, test_size=0.2, random_state=42):
    # 加载数据
    data = pd.read_excel(data_path)

    # 分割特征和标签
    X = data.iloc[:, :-1]  # 所有列除了最后一列
    y = data.iloc[:, -1]   # 最后一列

    # 划分训练集和测试集
    X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=test_size, random_state=random_state)

    # 创建朴素贝叶斯分类器
    # 1. ** priors: ** 先验概率，可以为None（默认）或array - like。如果为None，使用数据中的样本数来估计先验概率；如果为array - like，则指定每个类别的先验概率。
    # 2. ** var_smoothing: ** 方差平滑项，一个非负数。默认为1e - 9。用于稳定计算，避免概率为零的情况。
    # 在你提供的示例中，`model = GaussianNB(priors=[0.2, 0.3, 0.5], var_smoothing=1e-8)`
    # 意味着你在创建朴素贝叶斯分类器时，显式地指定了三个类别的先验概率为0.2、0.3和0.5，
    # 并设置了方差平滑项为`1e-8`，以确保概率计算的稳定性。
    model = GaussianNB(priors=[0.2, 0.3, 0.5], var_smoothing=1e-8)

    # 在训练集上训练模型
    model.fit(X_train, y_train)

    # 在测试集上进行预测
    y_pred = model.predict(X_test)

    # 计算准确率
    accuracy = accuracy_score(y_test, y_pred)
    return confusion_matrix(y_test, y_pred), y_test.values, y_pred, accuracy

if __name__ == "__main__":
    # 使用函数进行分类任务
    data_path = "iris.xlsx"
    confusion_mat, true_labels, predicted_labels, accuracy = naive_bayes_classification(data_path)

    print("真实值：", true_labels)
    print("预测值：", predicted_labels)
    print("准确率：{:.2%}".format(accuracy))

    # 绘制混淆矩阵
    plt.figure(figsize=(8, 6))
    sns.heatmap(confusion_mat, annot=True, fmt="d", cmap="Blues")
    plt.title("Confusion Matrix")
    plt.xlabel("Predicted Labels")
    plt.ylabel("True Labels")
    plt.show()

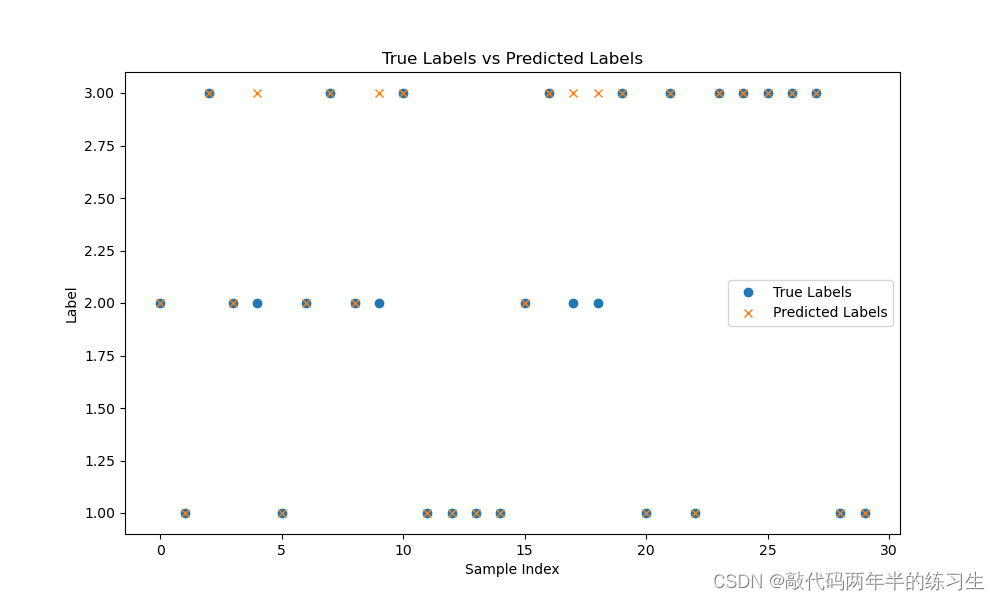
    # 用圆圈表示真实值，用叉叉表示预测值
    # 绘制真实值与预测值的对比结果
    plt.figure(figsize=(10, 6))
    plt.plot(true_labels, 'o', label="True Labels")
    plt.plot(predicted_labels, 'x', label="Predicted Labels")

    plt.title("True Labels vs Predicted Labels")
    plt.xlabel("Sample Index")
    plt.ylabel("Label")
    plt.legend()
    plt.show()

7.运行结果