前言

（1）今天看到一个有意思的问题，如何判断一个数字是否为2的若干次幂。这个问题并不难，但是对于我们的C语言功底还是有一点点的考验的。
（2）希望各位可以先自行思考，实在想不出来再看后面的讲解。提示，C语言的位运算是一个好东西。

解析

2的若干次幂数所存在的特征点

（1）首先，我们需要知道2的若干次幂所存在的特征点。当我们知道了这个特征点之后，就可以将这个特征点与其他数进行分离了。
（2）我们都知道，计算机是2进制系统。如果让一个数字乘以2，我们是不是可理解为，让这个二进制数右移动一位呢？

（3）既然我们知道了，在计算机中乘以2就是进行一次右移操作。那么2的n次幂，是不是就是二进制数1进行右移n次呢？例如，数字2换成二进制是10，而十进制的数字2恰好就是2的1次幂，因而二进制的1进行一次右移操作。
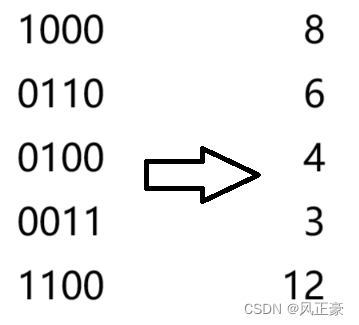
（4）好，我们再进行扩展，既然2的n次幂就是数字1进行右移n次。那么2的n次幂在二进制中是不是有一个特点，那就是只有一个位为1！（不理解的同学可以看一下下面这几个例子，我们发现2的n次幂的数8和4只有一个位为1）

如何提取这个特征点

（1）现在我们知道了2的若干次幂在二进制中，只会有一个位是1，其他位是数字0。因此，我们是不是得想个办法，判断一个二进制数只存在一个1。
（2）于是，我们可以想到"&"运算。他的特点在于，有0出0。假设我们的二进制数是100，那么让100减去1变成011。这样原来那个存放唯一数字1的地方就会变成0了。
（3）然后100&011，就会变成0。最后逻辑取反即可。

!((x)&(x-1))

（4）但是肯定有朋友会想举其他例子尝试反驳，很不幸的是你找不到的。
（5）为什么这么说呢？因为，我们要抓住这个方法的巧妙之处，我们是将唯一的存放1的位变成0。
（6）但是，我们假设有一个可以反驳的数1010。（注意，这里是假设）1010-1=1001，有没有发现一个问题，这里的最高位的数字1永远无法被消除。因此，进行如上操作之后，最终还是可以分辨出这不是2的n次幂。

上述代码存在bug？

bug1 — 不承认1为2的若干次幂

（1）看到上述代码，有一些东西肯定想到了一个刁钻的角度。数字1经过上述代码，最终输出的也是1啊。所以你这个代码有问题！这个时候我建议还是重新学一下小学数学啊（苦笑）。1就是2的0次幂呀。
（2）但是有一些朋友就是不承认1怎么办呢？也很简单，判断这个数是不是1呗。

x == 1 ? 0 : !((x)&(x-1))

bug2 — 数字0所导致的问题

（1）数字1导致的问题解决了，我们角度再刁钻一点，假设这个数字是0呢？真的可以吗？
（2）我们在Linux中执行如下代码。

#include <stdio.h>
#include <stdlib.h>

#define if_2_equation(x)  !((x)&(x-1))

int main(int argc,char** argv)
{
	char i;
	//如果输入参数小于2个，打印本程序使用方法
	if(argc < 2)
	{
		printf("Usage: \r\n");
		printf("%s <string> \r\n",argv[0]);
		return -1;
	}
	i = strtol(argv[1], NULL, 0);
	printf("number = %d \r\n",i);
	if(if_2_equation(i))
	{
		printf("yes\r\n");
	}
	else
	{
		printf("no\r\n");
	}
	return 0;
}

（3）执行发现，数字0也被当成了2的若干次幂，这个从数学的角度上来看，怎么也说不清楚啊。为什么会发生这种情况呢？很简单，0&所有的数，都是0。因此，这里就存在bug。
（4）怎么处理呢？很简单，进行一次判断呗。

#define if_2_equation(x)  x == 0 ? 0 : !((x)&(x-1))

（5）但是有些骚年会想，我1和0这两个数都不打算当成2的若干次幂来判断，这个怎么处理呢？也很简单，进行两次判断呗。

#define if_2_equation(x)  x == 0 ? 0 : (x == 1 ? 0 : !((x)&(x-1)))