一 什么是二叉搜索树
这个的结构特性非常重要,是后面函数实现的结构基础,二叉搜索树的特性是每个根节点都比自己的左树任一节点大,比自己的右树任一节点小。
例如这个图,

41是根节点,要比左树大,比右树小,满足但还不够,还要去看看41的左子树的根和右子树的根是否满足,更要判断这棵树上所有的根节点是不是都满足。而这棵树最厉害的地方之一我们用中序遍历(顺序左根右)便可以知道,遍历结果为13,15,17,22,28,33,37,41,42,50,53,58,61,66,78,排序不就排好了吗,复杂度可媲美快排和归并。二叉搜索树另一个功能那当然就是搜索了,例如我们要找66,66比根节点大,就不用去左子树找了,一下子少遍历一半,然后就去右子树找,和根节点58比较,66比58大,再去右子树找,再比较就找到了,最多查找高度次,满二叉树下为log(n)。而二叉搜索树是不是完美无缺,我也以为已经完美了,不好意思,我太年轻了,直到我看到下面这颗树。
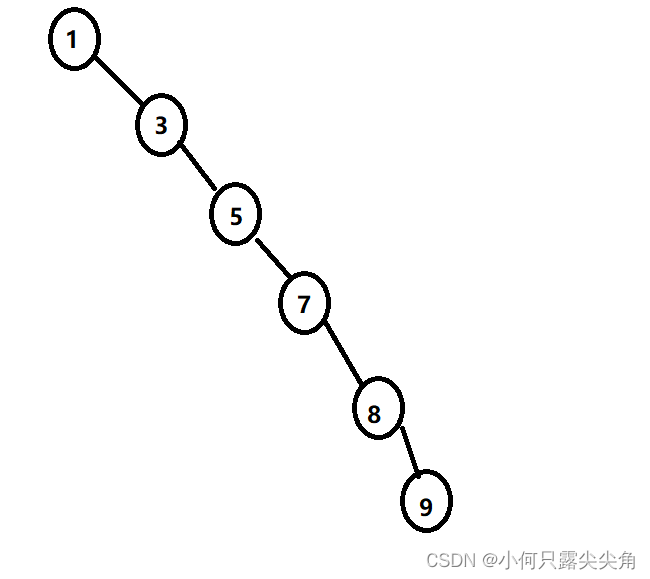
这个查找一次的效率就退化为O(N)了,解决办法:转化为平衡二叉树,通俗点就是换个根节点重新构造二叉树,例如把5或者7换成根节点,大家可以试试练习一下构建二叉树,构建完后的高度肯定比上图低,查找效率不就高了吗。
在说二叉搜索树的实现前,我们先说说什么是K结构,什么是KV结构,K结构就是只存一个数据,这个数据称为关键码,例如在英文词库里找一个英文单词,就是用关键码查找,需要的数据也是找到的关键码,但是KV结构就不同了,例如,通过拼音找汉字,这个时候拼音就是关键码,但是我们需要的数据不是拼音这个关键码,而是与之对应的汉字,这就是KV结构。
二 二叉搜索树K结构实现
1 树的节点类
template<class T>
struct TreeNode
{
TreeNode(const T& val)
:_val(val)//_val可能为自定义类型,在初始化列表初始化方便调用构造函数
{
;
}
TreeNode* left = nullptr;
TreeNode* right = nullptr;
T _val;
};2 BinaryTree树类
查找和排序都封装到了BinaryTree类中,和list一样,将节点类和树类分开封装。
(1) 默认构造函数
template<class T>
class BinaryTree
{
public:
typedef TreeNode<T> Node;
BinaryTree(Node*node=nullptr) 该构造函数是用节点指针初始化,
也可以再写个构造函数用个BinaryTree对象初始化
:_root(node)
{
;
}
private:
Node* _root = nullptr;树类只需根节点地址即可管理整棵树
};
(2) 拷贝构造函数
因为两个copy函数都是用递归遍历二叉树,所以只能再写一个子函数,毕竟外部无法传_root指针。
void copy1(Node*tree)//前序遍历加复用insert拷贝二叉树
{
if (tree == nullptr)
return;
insert(tree->_val); 先插入根节点的值,再去左子树和右子树获取节点的数值
insert内部会开辟空间
copy(tree->left);
copy(tree->right);
}
方法二比较巧妙的是它的第一个参数,root是外部传参_root的引用
所以root=new node(),可以直接修改根节点
而要拷贝左子树就传root->left的引用,这样new出来的节点可以直接连接到根的_left指针上。
右子树同理。
void copy2(Node*&root,Node*tree)
{
if (tree== nullptr)
return;
root = new Node(tree->_val);
copy2(root->left,tree->left);
copy2(root->right,tree->right);
}
BinaryTree(const BinaryTree<T>&tree)
{
//copy(tree._root);
copy2(_root, tree._root);
}copy2函数传指针引用我是受下面一个成员函数实现的启发,这个传引用一定要好好体会,方便理解后面的函数,非常巧妙。
(3) 赋值
用的是现代写法,比如t1,t2是两个BinaryTree对象,t1=t2就会调用下面的赋值函数,可是我的参数不是引用,那按规定自定义类型传值传参要用拷贝构造(我在类的成员函数博客曾提及),t2传参给tree就要调用拷贝构造,那tree就是一个新拷贝的对象,我们就可以用swap直接交换tree和t1的根节点指针,并且tree就是一个局部对象,函数调用完后会自动调用析构函数,省去了我们写析构t1树和创建新树的功夫,都给编译器做了。(string模拟的赋值也用到了现代写法)
void swap(BinaryTree<T>& tree)
{
std::swap(_root, tree._root);
}
void operator=(BinaryTree<T> tree)
{
swap(tree);
}
(4) find函数
搜索树怎么能缺少搜索功能呢
这个是find函数的子函数,子函数原因和上面同理,都是一开始传参外部无法获取_root,
因为递归遍历代码量少,所以我实现的是递归版本
bool _findR(Node*root,const T& val)
{
if (root == nullptr)
return false;
if (val > root->_val)//val比当前_val大,去右树找
{
return _findR(root->right, val);
}
else if (val < root->_val)//val比当前_val小,去左树找
{
return _findR(root->left, val);
}
else
{
return true;//val和当前_val相等,返回true
}
}
//下面这个是外部调用的find函数,只需要传要查找的值即可
bool find(const T& val)
{
return _findR(_root, val);
}
我之前在写find函数时,我还想着返回false是不是应该当左树和右树都没找到才返回false,好一会才醒悟,我们之所以去左树找,就是因为要找的val比根节点的值小,那右树更不会有了,所以左树找到nullptr就应该返回false,同理右树找到nullptr也返回false。
(5) insert函数
因为要递归去找合适的位置插入,所以同样要写一个子函数
void _insertR(Node*& root, const T&val)
{
if (root == nullptr)当找到空节点,就可以插入了,此时才是引用起作用的时候
{
root = new Node(val); 直接就可以修改了,因为root是上一个节点的left或者
right指针的引用。
return;
}
Node* cur = root;
if (val > cur->_val)//val大于当前根,插入到右树去
{
_insertR(cur->right,val);
}
else if (val < cur->_val)//val小于当前根,插入到左树去
{
_insertR(cur->left, val);
}
else
{
return;
}
}
void insert(const T& val)
{
_insertR(_root, val);
}(6) 中序遍历
void _Inorder(Node* root)//中序递归遍历
{
if (root == nullptr)
return;
_Inorder(root->left); 一直往左子树递归,直到左子树为空,算访问完,可以访问根。
cout << root->_val << " ";
_Inorder(root->right); 然后去右子树访问,同样分为左子树,根,右子树
}
void Inorder()
{
_Inorder(_root);//调用子函数,外部无法获取私有成员_root
}
(7) erase函数
bool _Rerase(Node*&root,const T&val)
{
if (root == nullptr)
return false;
Node* cur = root;
if (val > root->_val)//用_val找节点
{
return _Rerase(root->right, val);
}
else if (val < root->_val)
{
return _Rerase(root->left, val);
}
else//找到了
{
//该节点只有一个或者无子节点
if (root->left == nullptr) 由于root是上一节点左指针或者右指针的别名,
所以可以直接拿root->right来赋值给root,否则还要
判断root->right是链接在上一节点的left指针还是
right指针。
{
root = root->right;
}
else if (root->right == nullptr)
{
root = root->left;
}
else
{
删除有两个子节点的节点-替换法
找该节点左子树中最大的,或者右子树中最小的来替换删除节点
Node* leftMax = root->left;
while (leftMax->right)
{
leftMax = leftMax->right;
}
std::swap(leftMax->_val, root->_val);
return _Rerase(root->left, val);
调用_Rerase去删除leftMax节点,
这里必须要传root->left,去左子树删除值为val的节点,不能传root
例如我们交换leftMax的7和root的8值,如果传root,8的值比7大,就会去右树删,
就找不到leftMax节点了,但是root的左子树仍然满足二叉搜索的特性,就可以找到leftMax节点并删除。
}
delete cur; 该处统一释放删除节点,并返回true
return true;
}
}
bool erase(const T& val)//删除某个节点
{
return _Rerase(_root, val);
}
三 kv结构实现
本来我以为kv结构是要将K结构的树大改,当我实现后才发现,赋值可以直接照搬,,find,insert,erase中大量的if判断都是用关键码判断,根本不需要改动,中序遍历也就多打印一个数据,还有insert和拷贝构造函数要在new一个节点的时候多传一个参数。
接下来就看看一些比较重要的改动,在这里_key存关键码,而我上面二叉树K结构中是_val存的关键码,不要搞混了。
1 树的节点类
template<class T,class K>
struct TreeNode
{
TreeNode(const T& val,const K&key)
:_val(val)
,_key(key)
{
;
} 类内可不加模板参数,也就是说TreeNode等价于TreeNode<T,k>
TreeNode* left = nullptr;
TreeNode* right = nullptr;
T _val;//存与关键码对应的数据
K _key;//_key存关键码
};2 BinaryTree类
有了先前K结构树的基础,这里构造和析构函数我们就很好理解。
(1)构造和析构函数
template<class T, class K>
class BinaryTree
{
public:
typedef TreeNode<T,K> Node;
BinaryTree(Node* node = nullptr) 默认构造无改变
:_root(node)
{
;
}
void _DestroyR(Node*&root) 递归释放节点,采用后序遍历的方式delete
{
if (root == nullptr)
return;
_DestroyR(root->left);
_DestroyR(root->right);
delete root;
root = nullptr;
}
~BinaryTree()
{
_DestroyR(_root);
}
private:
Node* _root = nullptr; 成员变量是不变的,毕竟kv结构的树用根节点同样可以管理
};
}
(3)erase函数
bool _Rerase(Node*& root, const T& key)
{
if (root == nullptr)
return false;
Node* cur = root; //记录节点,方便后面delete
if (key > root->_key)
{
return _Rerase(root->right,key);
}
else if (key <root->_key)
{
return _Rerase(root->left, key);
}
else//找到了
{
//该节点只有一个或者无子节点
if (root->left == nullptr)
{
root = root->right;
}
else if (root->right == nullptr)
{
root = root->left;
}
else
{
Node* leftMax = root->left;
while (leftMax->right)
{
leftMax = leftMax->right;
}
std::swap(leftMax->_val, root->_val); 在交换时要多交换一个值
std::swap(leftMax->_key, root->_key);
return _Rerase(root->left, key); 并且还是用key值去找leftMax删
} 删除完leftMax后就直接return了,就不会重复删除。
delete cur;
return true;
}
}
bool erase(const T& val)//删除某个节点
{
return _Rerase(_root, val);
}二叉搜索树中最复杂的就是erase函数,大家在此处一定要画图理解。