Codeforces Round 891 (Div. 3)
目录
- A. Array Coloring
- 题目大意
- 思路
- 代码
- B. Maximum Rounding
- 题目大意
- 思路
- 代码
- C. Assembly via Minimums
- 题目大意
- 思路
- 代码
A. Array Coloring
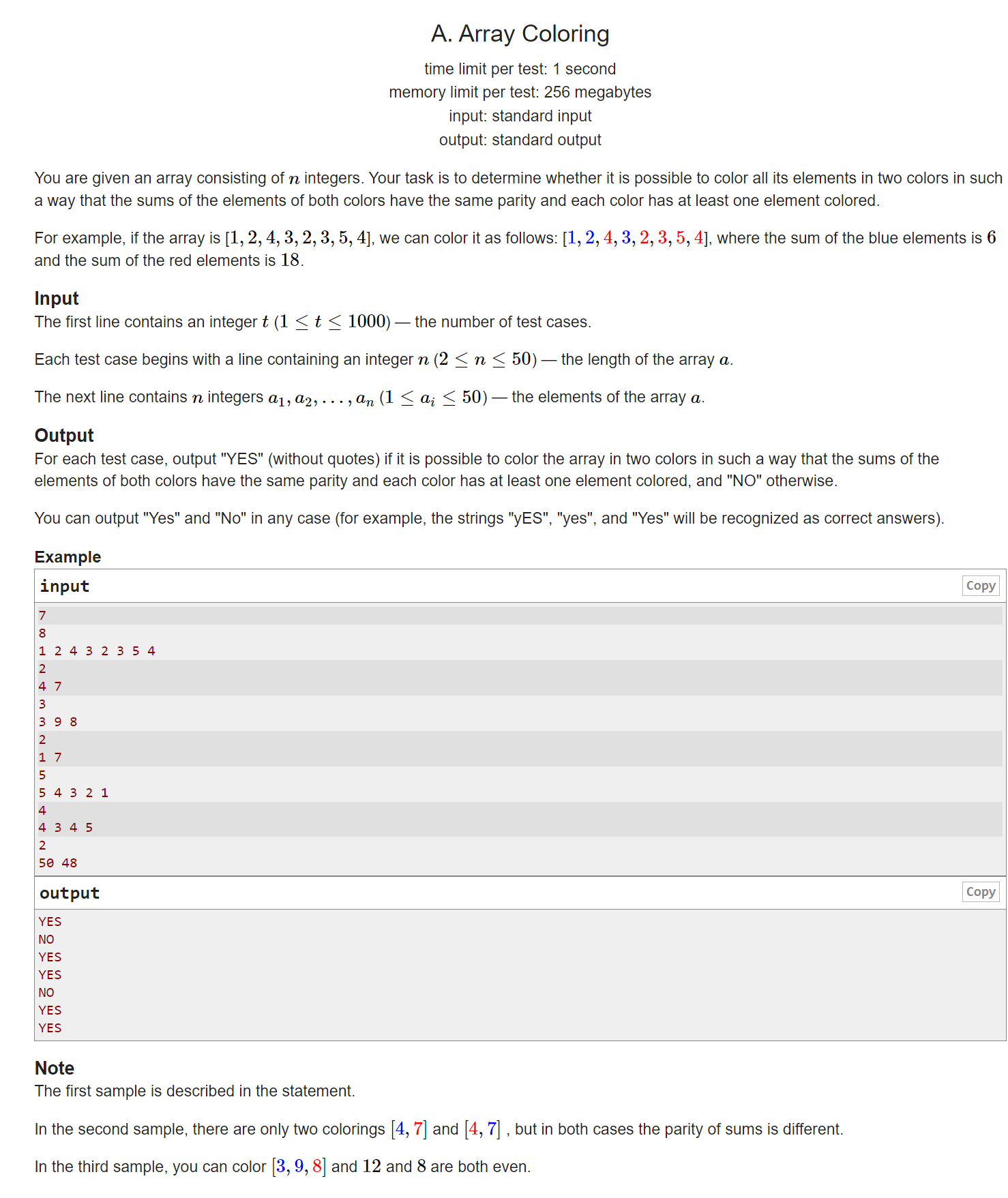
题目大意
给你一个包含 n n n个数字的数组,你的任务是判断这个数组是否可以划分成两个子数组,使得子数组的和奇偶同性。
翻译:
给定一个由n个整数组成的数组。您的任务是确定是否有可能以两种颜色为其所有元素上色,从而使两种颜色的元素的和具有相同的奇偶性,并且每种颜色至少有一个元素上色。
例如,如果数组是[1,2,4,3,2,3,5,4],我们可以这样给它上色:[1,2,4,3,2,3,5,4],蓝色元素的和是6,红色元素的和是18。
输入第一行包含一个整数t(1≤t≤1000)—测试用例的个数。
每个测试用例以包含整数n(2≤n≤50)的行开头,即数组a的长度。
下一行包含非整数a1,a2,…,an(1≤ai≤50)-数组a的元素。
输出
对于每个测试用例,如果可以用两种颜色为数组上色,并且两种颜色的元素的和具有相同的奇偶性并且每种颜色至少有一个元素上色,则输出“YES”(不带引号),否则输出“NO”。
您可以在任何情况下输出“Yes”和“No”(例如,字符串“Yes”、“Yes”和“Yes”将被识别为正确答案)。
思路
这道题题题目的关键在于奇偶同性,我们都知道
奇数+奇数=偶数
奇数+偶数=奇数
偶数+偶数=偶数
所以这道题目就可以转化为数组中奇数的个数,如果是奇数个,就不成立,否则就成立。
代码
#include<bits/stdc++.h>
using namespace std;
int main()
{
int t;
cin>>t;
while(t--)
{
int n;
scanf("%d",&n);
long long sum=0;
for(int i=0;i<n;++i)
{
int shuru;
scanf("%d",&shuru);
sum+=shuru;
}
if(sum%2==0)printf("YES\n");
else printf("NO\n");
}
return 0;
}
B. Maximum Rounding

题目大意
太复杂了,直接上翻译
翻译:
给定一个自然数x,可以执行如下操作:
选择一个正整数k,将x四舍五入到第k位。请注意,这些位置是从右到左编号的,从0开始。如果数字有k位,则认为第k位的数字等于0。
舍入方法如下:
如果第(k−1)位的数字大于或等于5,则第k位的数字增加1,否则第k位的数字保持不变(使用数学四舍五入)。如果在操作之前,第k位的数字是9,它应该加1,那么我们搜索最小的位置k
’ (k ’ >k),其中第k位的数字小于9,并在第k位的数字上加1。然后赋值k=k ’ 之后,所有位置小于k的数字都被替换为0。
你的任务是使x尽可能的大,如果你可以执行尽可能多的操作的话。例如,如果x等于3451,那么如果连续选择:
K =1,那么运算后x将变成3450 K =2,那么运算后x将变成3500 K =3,那么经过运算后x将变成4000 K
=4,那么运算后x将变成0 为了使答案最大化,你需要先选择k=2,然后k=3,然后这个数字就变成了4000。 输入 第一行包含一个整数t(1≤t≤104)——测试用例的数量。每个测试用例由长度不超过2⋅105的正整数x组成。可以保证该整数中没有前导零。
保证所有整数×所有测试用例的长度之和不超过2⋅105。
输出 对于每组输入数据,在操作后输出x的最大可能值。数字的表示形式不应有前导零。
思路
从前往后进行判断,一旦识别到大于等于5的数就可以进行操作了,因为后面的数字再怎么样操作都不会比当前的操作更大,而且操作完当前这一位的数字之后后面的数字会清空变成0,所以我们只需要操作第一个大于对等于 5的数就好了,这里还需要注意一个特殊的情况,那就是当前的数操作完之后要判断前面的数增加1之后是否大于等于5,也就是前面的数字原本是4的情况,以及全部的数字操作完之后总共的位数可能会增加一,注意这两个地方就可以了。
代码
#include<bits/stdc++.h>
using namespace std;
int main()
{
int t;
cin>>t;
while(t--)
{
string s;
cin>>s;
//char a[(int)(2*1e5+10)]{0};
int zhizhen=0;
int yishuchu=0;
bool pd=0;
for(int i=0;i<(int)s.size();++i)
{
if(s[i]>='5')
{
for(int j=i+1;j<s.size();++j)
{
s[j]='0';
}
for(int j=i-1;j>=0;--j)
{
if(s[j+1]>='5')
{
s[j]=s[j]+1;
s[j+1]='0';
// cout<<"******\n";
// for(int i=0;i<s.size();++i)
// cout<<s[i];cout<<endl;
}
else
{
break;
}
}
//if(s[])
}
}
if(s[0]<='4')
{
for(int i=0;i<s.size();++i)
cout<<s[i];cout<<endl;
}
else
{
printf("1");
for(int i=0;i<s.size();++i)
cout<<0;cout<<endl;
}
}
return 0;
}
C. Assembly via Minimums

题目大意
对一个长度为n的数组a进行操作,任意两个数之间取最小值,得到一个长度为n*(n-1)/2 的数组b,现在知道数组b,求数组a的可能是哪些数字组成。
翻译:
Sasha有一个包含n个整数的数组a。他觉得很无聊,他得到了一个大小为n·(n−1)2的新数组b。
例如,如果一个=(2、3、5、1),他会写[min(2、3),最小值(2、5)、min(2,
1),最小值(3、5)、min(3,1),最小值(1)]=[2 2 1、3、1、1]。然后,他随机洗牌数组b的所有元素。
不幸的是,他忘记了数组a,你的任务是恢复任何可能的数组a,从这些数组a中可以得到数组b。
数组a的元素应该在[−109,109]的范围内。
输入 第一行包含一个整数t(1≤t≤200)——测试用例的数量。
每个测试用例的第一行包含一个整数n(2≤n≤103)——数组a的长度。
每个测试用例的第二行包含n⋅(n−1)2个整数b1,b2,…,bn⋅(n−1)2(−109≤bi≤109)-数组b的元素。
可以保证n对所有测试的和不超过103,并且对于测试中的每个数组b,都存在一个原始数组。
输出 对于每个测试用例,输出任意长度为n的数组a。
思路
首先来分析数组a中最小的数字,假设为x,则x在数组b里面出现的次数肯定是n-1次,然后就是第二小的数字,出现的次数肯定是n-2次,第三小的数字出现的次数肯定是n-3次…以此类推,所以直接排序就能得到原来的数组。
代码
#include<bits/stdc++.h>
using namespace std;
int arr[(int)1e6+10]{0};
int cmp(int a,int b)
{
return a<b;
}
int main()
{
int t;
cin>>t;
while(t--)
{
int n;
scanf("%d",&n);
for(int i=0;i<n*(n-1)/2;++i)
{
scanf("%d",&arr[i]);
}
sort(arr,arr+(n*(n-1)/2),cmp);
int zhizhen=0;
for(int i=n-1;i>0;--i)
{
printf("%d ",arr[zhizhen]);
zhizhen+=i;
}
// cout<<"***\n";
// for(int i=0;i<n*(n-1)/2;++i)
// cout<<arr[i]<<' ';cout<<endl;
printf("%d\n",arr[zhizhen-1]);
}
return 0;
}