面对需求的不确定性,报童模型是做库存优化的常见模型。而标准报童模型假设价格是固定的,此时求解一个线性规划问题,可以得到最优订货量,这种模型存在局限性。因为现实世界中价格与需求存在一定的关系,本文假设需求q是价格p的线性函数,基于历史需求数据学习回归直线的参数并计算拟合残差,带入到报童模型中,此时的报童模型变成一个二次规划问题,其目标函数是关于价格p是二次的。
方法
为提高报童模型的准确性,使用SAA算法解决随机优化问题,并与其他方法做对比。
对标准报童模型做的三个扩展
扩展1:允许rush order
当售卖当天需求量过高时,允许报童紧急订报,只是价格g比一般订购价格c稍高,即g>c;
如果定货太多,那么每份报纸会产生持货成本t,特别地,如果允许以一定价格回退给厂商,那么t<0 。但在这个文章中,仅考虑t>0的情况。
符号说明:
单份报纸的售价为p;
订货量是q;
目标函数是
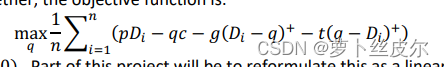
扩展2:需求与价格呈线性相关
假设需求与价格的线性回归模型如下
D
=
β
0
+
β
1
p
+
ϵ
i
D=\beta_0+\beta_1p+\epsilon_i
D=β0+β1p+ϵi
根据给定的数据集(含价格和需求量,即
{
(
p
i
,
D
i
)
∣
i
=
1
,
2
,
.
.
.
,
n
}
\{(p_i,D_i)|i=1,2,...,n\}
{(pi,Di)∣i=1,2,...,n}),找出最佳拟合线性回归函数的参数。假设干扰项
ϵ
i
\epsilon_i
ϵi具有随机性,根据历史数据
{
(
p
i
,
D
i
)
∣
i
=
1
,
2
,
.
.
.
,
n
}
\{(p_i,D_i)|i=1,2,...,n\}
{(pi,Di)∣i=1,2,...,n}学习到参数
β
0
,
β
1
\beta_0,\beta_1
β0,β1,计算残差值
{
ϵ
i
∣
i
=
1
,
2
,
.
.
.
,
n
}
\{\epsilon_i|i=1,2,...,n\}
{ϵi∣i=1,2,...,n}。
- 对于价格固定的标准报童模型,求最优订货量
如果新价格p出现,将计算好的残差值 { ϵ i ∣ i = 1 , 2 , . . . , n } \{\epsilon_i|i=1,2,...,n\} {ϵi∣i=1,2,...,n}和新价格p带入模型 D = β 0 + β 1 p + ϵ i D=\beta_0+\beta_1p+\epsilon_i D=β0+β1p+ϵi,可以得到新价格p所对应的需求量估计值 { D i ^ ∣ i = 1 , 2 , . . . , n } \{\hat{D_i}|i=1,2,...,n\} {Di^∣i=1,2,...,n},这些估计值会带入到标准报童模型中,求解该线性规划问题,从而得到最优订货量。
关于计算需求量估计值的进一步解释,比如:估计参数 β 0 = 1000 , β 1 = − 2 \beta_0=1000,\beta_1=-2 β0=1000,β1=−2,现有两个样本的拟合残差是15和-9,对于新价格2来说,需求量估计值有
1000 − 2 ∗ 2 + 15 = 1011 1000-2*2+15=1011 1000−2∗2+15=1011,
1000 − 2 ∗ 2 − 9 = 987 1000-2*2-9=987 1000−2∗2−9=987 - 对于价格不固定的扩展报童模型,求最优订货量和最优价格
此时,目标函数
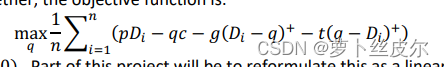
中 p ∗ D i p*D_i p∗Di就会变成 p ∗ ( β 0 + β 1 p + ϵ i ) p*(\beta_0+\beta_1p+\epsilon_i) p∗(β0+β1p+ϵi),这是价格p的二次函数。
注意:上面目标函数中的 D i D_i Di指的是新价格p所对应的第i个需求估计值,而不是原数据集中第i个样本的需求值。
我觉得没有疑问了,这本身就是一个关于价格p的二次优化问题。
注:
为了求解这个问题,引入哑变量
h
i
h_i
hi,表示第i天成本的负值。如此一来,目标函数——利润函数可以表示为收益+成本负值的平均,其中收益指
p
∗
D
i
p*D_i
p∗Di,成本负值指
h
i
h_i
hi。


扩展3:分析数据集对最优订货量和最优价格的影响(最优订购量、最优价格的敏感性分析)
对原数据集做重采样,计算最优订货量、最优价格、对应的期望利润值。
任务
- 根据给定数据集,估计出需求与价格之间的线性回归方程;
- 给定参数c=0.5,g=0.75,t=0.15,利用残差数据 { ϵ i ∣ i = 1 , 2 , . . . , n } \{\epsilon_i|i=1,2,...,n\} {ϵi∣i=1,2,...,n},求价格p=1时的需求量估计值 { D i ^ ∣ i = 1 , 2 , . . . , n } \{\hat{D_i}|i=1,2,...,n\} {Di^∣i=1,2,...,n};
- 求价格p=1时的最优订货量(这是一个线性规划问题);
- 假设价格不是固定的,将需求量与价格的线性回归方程带入到报童模型中,解QP(二次规划问题,目标函数含价格的平方项),得最优订货量、最优价格;
- 分析最优价格、最优订货量是否对数据集敏感。对原数据集做重采样,重新估计需求与价格之间的线性回归函数参数 ,求最优价格和最优订货量;
- 重复上述重采样、拟合操作,得到多组最优订货量和最优价格;为得到的最优订货量、最优价格、期望利润绘制直方图,观察统计规律。
建模
价格固定时
下面是思路,我用黄色荧光笔标了步骤,即
如果新价格p出现,将计算好的残差值
{
ϵ
i
∣
i
=
1
,
2
,
.
.
.
,
n
}
\{\epsilon_i|i=1,2,...,n\}
{ϵi∣i=1,2,...,n}和新价格p带入模型
D
=
β
0
+
β
1
p
+
ϵ
i
D=\beta_0+\beta_1p+\epsilon_i
D=β0+β1p+ϵi,可以得到新价格p所对应的需求量估计值
{
D
i
^
∣
i
=
1
,
2
,
.
.
.
,
n
}
\{\hat{D_i}|i=1,2,...,n\}
{Di^∣i=1,2,...,n},这些估计值会带入到标准报童模型中,求解该线性规划问题,从而得到最优订货量。
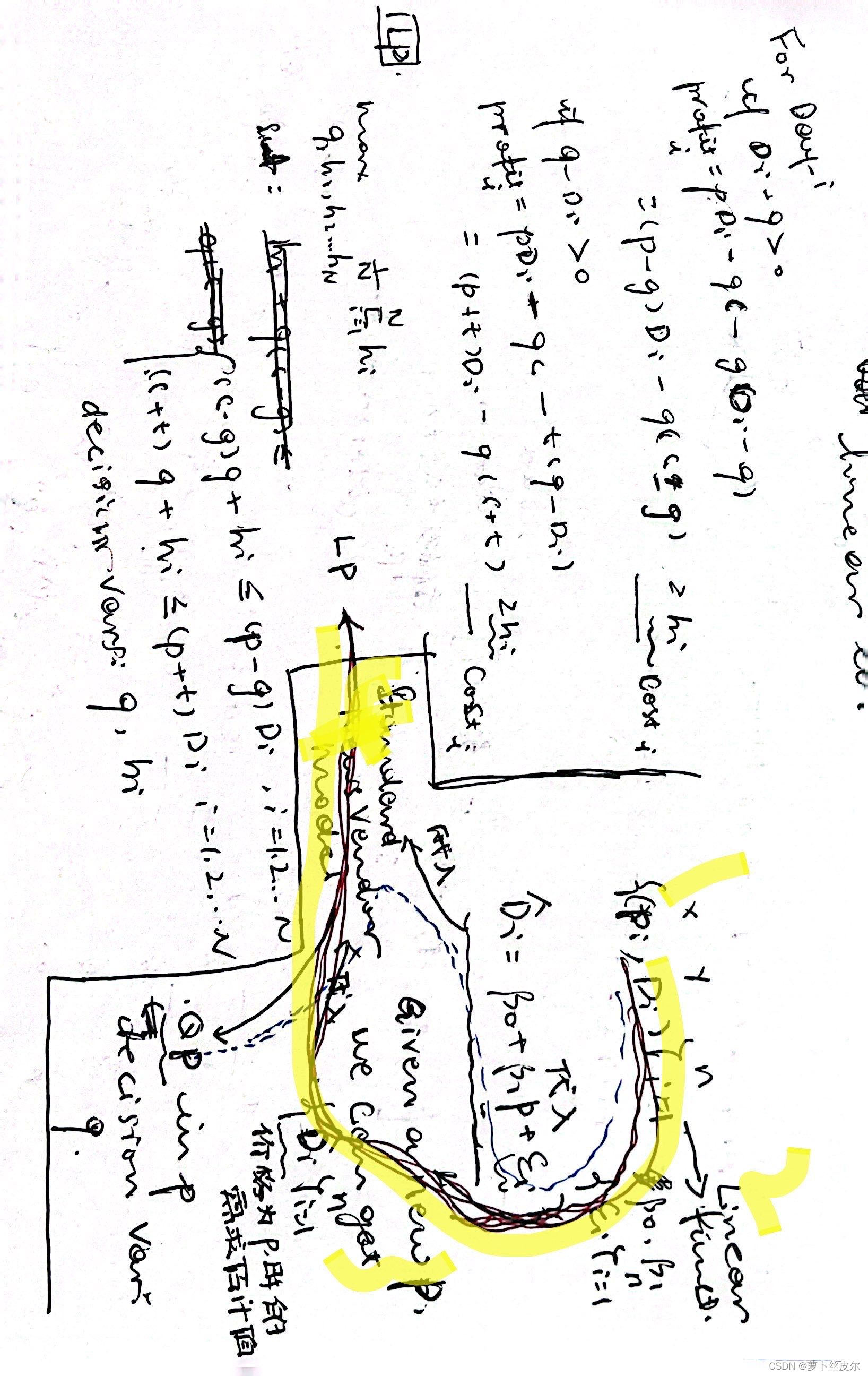

上述模型的含义:目标函数是最大化利润,引入哑变量
h
i
h_i
hi表示第’i天的成本负值。
上面画黄线的约束表示:不管需求量大于还是小于订货量,利润都大于
h
i
h_i
hi。换言之,限制利润(不管需求量大于还是小于订货量)大于等于一个变量,这个变量大于等于负无穷。
??为什么成本负值数组h的约束不是
0
>
h
>
−
inf
0>h>-\inf
0>h>−inf 做实验的时候,加上试试。会影响结果
将上述约束化简成Gurobi建模所需要的形式(如下图的蓝笔)
注:“Gurobi建模所需要的形式”是指“明确哪些是决策变量,哪些是决策变量的系数,哪些是右端项”,这里的决策变量有
q
,
h
1
,
.
.
.
h
N
q,h_1,...h_N
q,h1,...hN。
化简步骤见图中黑笔
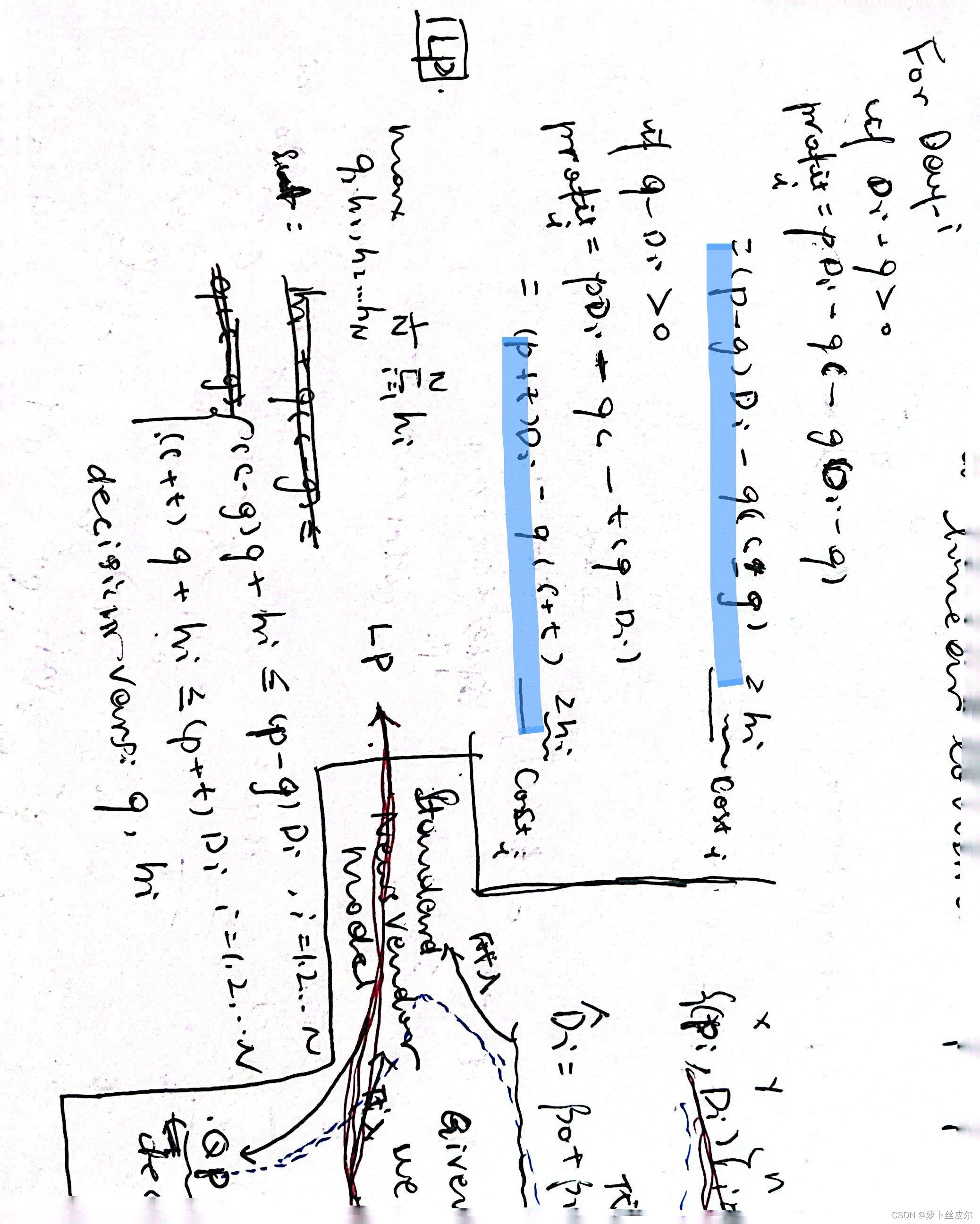
价格不固定时
我用蓝笔标注了步骤:
首先,获取需求-价格数据集,估计线性回归参数并计算残差数据;
接着,把
D
=
β
0
+
β
1
p
+
ϵ
i
D=\beta_0+\beta_1p+\epsilon_i
D=β0+β1p+ϵi带入到标准报童模型中,会得到一个二次规划问题。
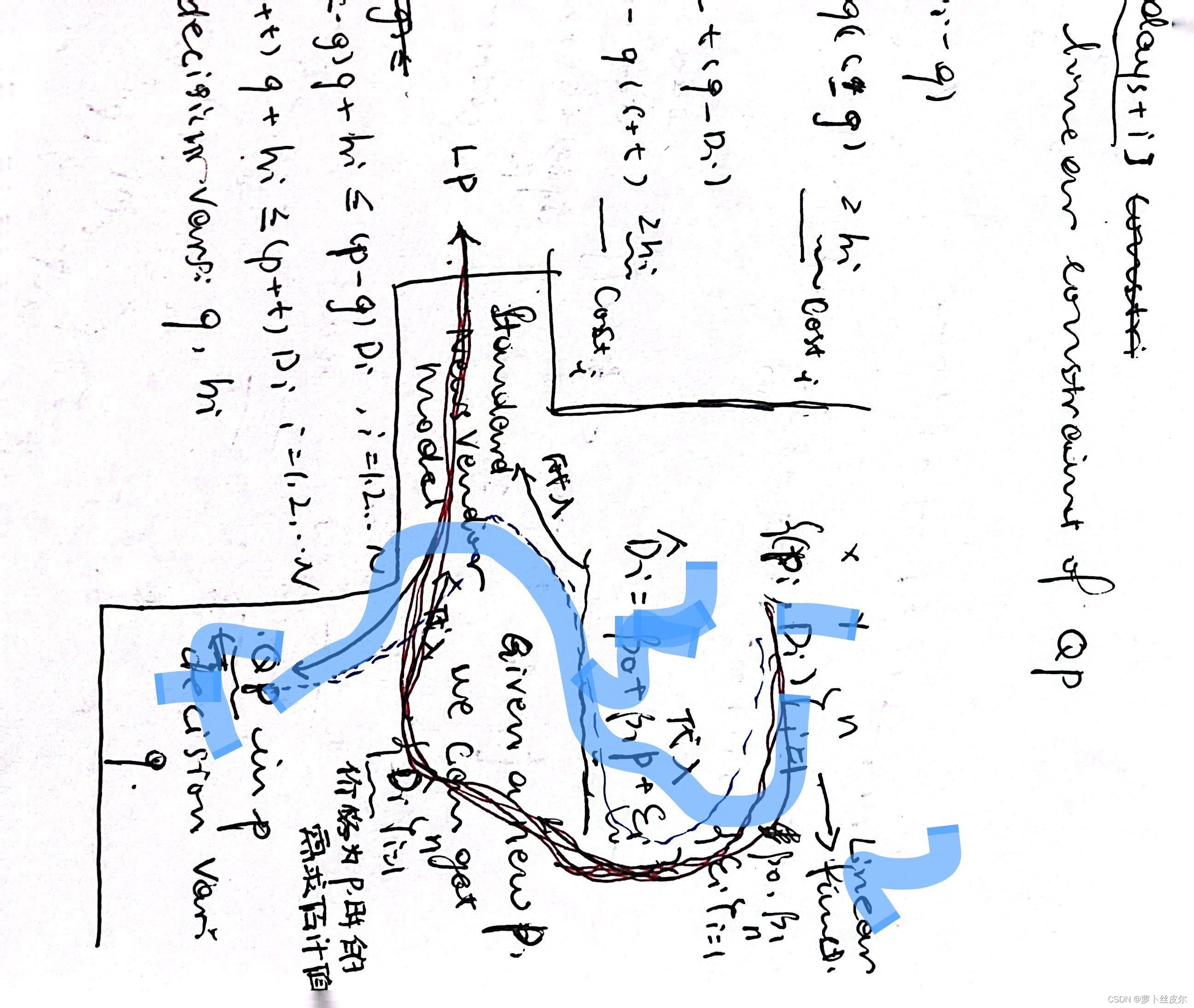
将之前的拟合结果——残差数据、拟合函数参数等,带入到上述模型中,得到需求量估计值 D i D_i Di,得到如下模型:
记录一个我没看懂的地方。我觉得作者的转换并没有把二次约束转成线性约束啊,难道是我对“二次规划”的定义理解出错了?我以为的二次规划是,目标函数是二次的,约束是一次的 数学优化问题。

关于上图的问题,我在纸上列了一下,作者的Gurobi模型应该是把上面两个约束的二次项
p
2
p^2
p2拿掉了(用报告里面的话说:拿到目标函数中了)。
??为什么可以直接拿掉呢
关于上面的约束如何化简成jupyter文件中Gurobi模型,我在草稿纸上简单列了一下,蓝色荧光笔标注的是Gurobi建模时所用的约束。
约束1:

约束2:

上图还有一个问题是,目标函数中决策变量
h
i
h_i
hi的系数应该是1。这一点可以从两个地方看出来:第一,老师给的作业说明(见上面“扩展2”中,
h
i
h_i
hi的含义说明——成本负值);第二,作者的Gurobi建模obj数组中目标函数系数的指定。
最优解的稳定性分析
目标:探究使用不同的数据集是否会影响到最优解——最优价格和最优订货量
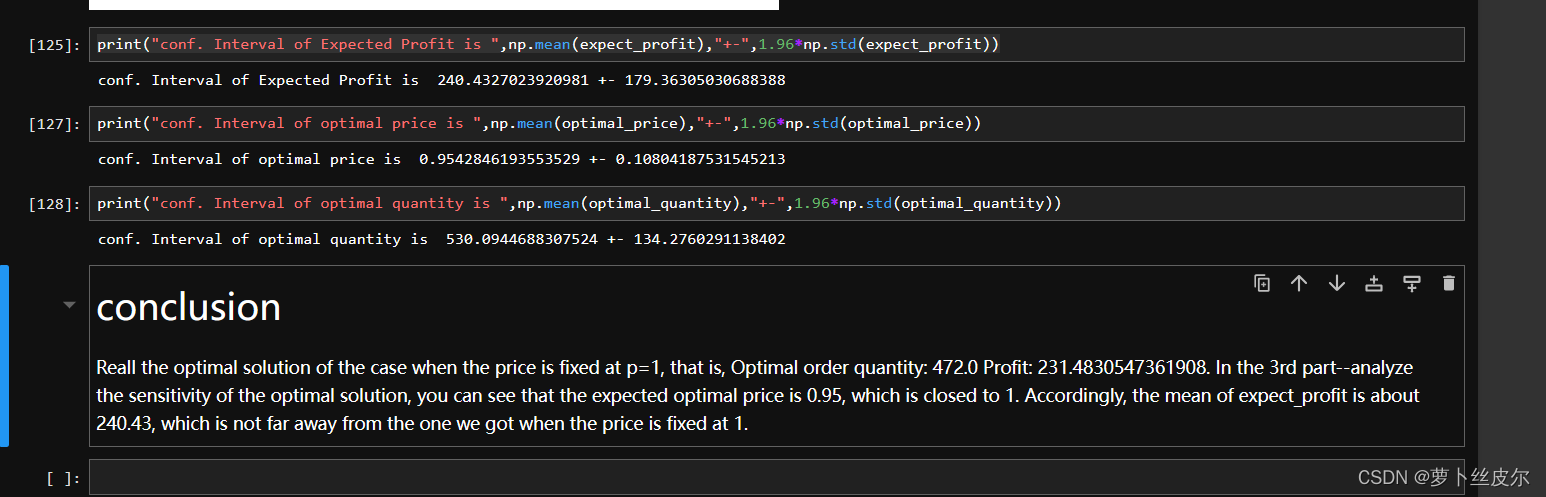
做法:对原数据集做1000次重采样,每次采样随机抽取99组样本形成新数据集。然后,针对新数据集,计算并收集最优订货量和最优价格,以及对应的最优利润expect_profit。绘制最优订货量、最优价格、最优价格的分布直方图,发现大致服从正态分布,且最优价格与之前LP中的预定价格1相差不大,expect_profit的均值也与之前LP的expect_profit相差不大。
注:新数据集与原数据集样本顺序是不同的。(我觉得这里有些不妥……应该设计新数据集是原数据集的子集,然后观察最优解的统计规律)
我给这个报告添加了一个conclusion,如下图