1005 0 vs 1

双端队列暴力模拟,时间复杂度为O(n*T)

首先预处理0的右边第一个0的下标,1的右边第一个1的下标,0的左边第一个0的下标,1的左边第一个1的下标

然后进行模拟

如果当前是zero的轮次,那么就看双端队列的两端

如果两头都是1,那么one赢,如果1头是0,1头是1,那么只能选择0

如果两头都是0,那么我们就要判断选择哪一个0,我们就贪心,想着能快点到达下一个0,所以就比较哪个0到下一个0的距离更近,我们就选择哪一个0,这样的话,首先对于zero来说,可以更快地到达下一个0,同时,掌握了主动权,因为zero选择哪一边,one就得跟着选择哪一边,那么当两边的0到达下一个0的距离相同时,我们就随便选择一边的0就行,因为两头对称,选择哪一头都一样,而且反正主动权在zero手上,zero不管选择哪边,one都只能跟着选同一边

对于one,同理

最后如果都没有输,那么平局,输出-1

AC代码:

#include<iostream>
#include<algorithm>
#include<cstring>
#include<vector>
#include<deque>
#include<cmath>
#include<cstdio>
#define endl '\n'
//#define int long long
using namespace std;
typedef long long ll;
const int N=1e5+10;
char a[N];
int l1[N],l2[N];//存放0的右边第一个0的下标,以及1的右边第一个1的下标
int r1[N],r2[N];//存放0的左边第一个0的下标,以及1的左边第一个1的下标
int n;
void solve() {
    cin>>n;
    deque<int>q;
    for(int i=1; i<=n; i++) cin>>a[i];

    //预处理
    int x=0,y=0;
    for(int i=1; i<=n; i++) {
        if(a[i]=='0') {
            l1[x]=i;
            x=i;
        } else {
            l2[y]=i;
            y=i;
        }
    }
    x=n+1,y=n+1;
    for(int i=n; i>=1; i--) {
        if(a[i]=='0') {
            r1[x]=i;
            x=i;
        } else {
            r2[y]=i;
            y=i;
        }
    }
//    cout<<"="<<endl;
    for(int i=1; i<=n; i++) q.push_back(i);
    int turn=0;//表示到谁操作了
    while(q.size()) {
        if(turn==0) {
            turn=1;
            if(a[q.front()]=='1'&&a[q.back()]=='1') {
                cout<<1<<endl;
                return;
            } else if(a[q.front()]=='1'||a[q.back()]=='1') {
                if(a[q.front()]=='0') q.pop_front();
                else q.pop_back();
            } else {
                if(l1[q.front()]-q.front()<=q.back()-r1[q.back()]) q.pop_front();
                else q.pop_back();
            }
        } else {
            turn=0;
            if(a[q.front()]=='0'&&a[q.back()]=='0') {
                cout<<0<<endl;
                return;
            } else if(a[q.front()]=='0'||a[q.back()]=='0') {
                if(a[q.front()]=='1') q.pop_front();
                else q.pop_back();
            } else {
                if(l2[q.front()]-q.front()<=q.back()-r2[q.back()]) q.pop_front();
                else q.pop_back();
            }
        }
    }
    cout<<-1<<endl;
    return;
}
int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int t=1;
    cin>>t;
    while(t--)
        solve();
    return 0;
}

1007 Solubility

就是n种液体,一共有m种互溶关系,然后判断所给的k种液体是否可以全部互溶

并查集,将有互溶关系的液体放在同一个联通块中,然后判断给定的k种液体是否全部在同一个连通块中

AC代码:

#include<iostream>
#include<algorithm>
#include<cstring>
#include<vector>
#include<deque>
#include<cmath>
#include<cstdio>
#define endl '\n'
//#define int long long
using namespace std;
typedef long long ll;
const int N=1e5+10;
int p[N];
int find(int x){
    if(p[x]!=x) p[x]=find(p[x]);
    return p[x];
}
int n,m;
void solve() {
    cin>>n>>m;
    for(int i=1;i<=n;i++) p[i]=i;
    for(int i=0;i<m;i++){
        int u,v;
        cin>>u>>v;
        u=find(u),v=find(v);
        if(u!=v) p[u]=v;
    }
    int k;
    cin>>k;
    bool flag=true;
    int x;
    cin>>x;
    int ans=find(x);
    for(int i=1;i<=k-1;i++){
        cin>>x;
        if(find(x)!=ans){
            flag=false;
        }
    }
    if(flag) cout<<"YES"<<endl;
    else cout<<"NO"<<endl;
}
int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int t=1;
    cin>>t;
    while(t--)
        solve();
    return 0;
}

两种错误：

错误1:数有几个节点x满足p[x]==x,那么就有几个连通块,如果n个节点都枚举到,那么是对的,因为枚举到了所有的祖宗节点,但是单单枚举其中的k个节点,这样写是有问题的,因为可能没有枚举到祖宗节点,那么都不会计入连通块的个数

    int k;
    cin>>k;
    int cnt=0;
    for(int i=1;i<=k;i++){
        int x;
        cin>>x;
        if(p[x]==x) cnt++
    }
    if(cnt==1) cout<<"YES"<<endl;
    else cout<<"NO"<<endl;

错误2:写了个break,如果只有一个样例,那么是没问题的,直接输出答案,后面不输入也没有关系,但是有t个样例,如果break了,该样例还未输入的数据可能会用于下一个样例中 

 int k;
    cin>>k;
    bool flag=true;
    int x;
    cin>>x;
    int ans=find(x);
    for(int i=1;i<=k-1;i++){
        cin>>x;
        if(find(x)!=ans){
            flag=false;
            break;
        }
    }
    if(flag) cout<<"YES"<<endl;
    else cout<<"NO"<<endl;

1010 Rikka with Square Numbers

将平方数依次列举出来,发现两两相邻的平方数相减会得到奇数,通过这样的操作,我们可以得到任意的奇数(其中1本身就是平方数)

 

 

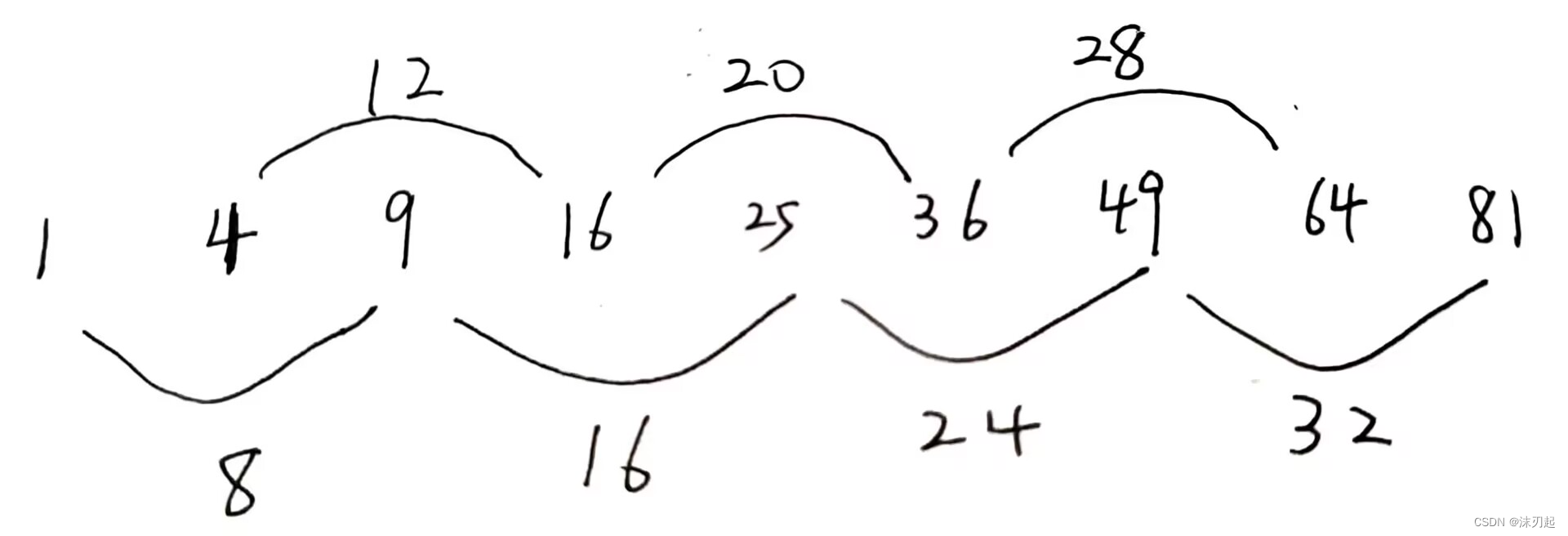
然后由于1本身就是平方数,又因为我们可以得到任意一个奇数,故可以通过+1或者-1得到任意一个偶数

令diff为a和b的差的绝对值,然后我们看最少需要几个平方数能凑出n

如果diff本身为平方数,那么操作次数即为1

如果diff可以分解为两个平方数的和,那么操作次数为2

如果diff是4的倍数,就可以分解为两个平方数的差,操作次数为2

如果diff为奇数但又不能分解为两个平方数的和,那么可以通过两个平方数凑出该奇数,那么操作次数为2

如果diff为偶数但又不能分解为两个平方数的和,那么可以通过两个平方数和一个1凑出该偶数,那么操作次数为3

AC代码: 

#include<iostream>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<vector>
#include<cstdio>
#define endl '\n'
//#define int long long
using namespace std;
typedef long long ll;
int a,b;
bool check(int x){
    int t=(int)sqrt(x);
    if(t*t==x) return true;
    return false;
}
int solve() 
{
    cin>>a>>b;
    int diff=abs(a-b);
    if(check(diff)) return 1;
    for(int i=1;i*i<=diff/2;i++){
        int j=diff-i*i;
        if(check(j)) return 2;
    }
    if(diff%2==1) return 2;
    if(diff%4==0) return 2;
    return 3;
}
int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int t=1;
    cin>>t;
    while(t--)
        cout<<solve()<<endl;
    return 0;
}