import cv2 as cv
import numpy as np
import matplotlib.pyplot as plt
img_cat = cv.imread("../SampleImages/cat.jpg", cv.IMREAD_COLOR)
plt.imshow(img_cat[:,:,::-1])
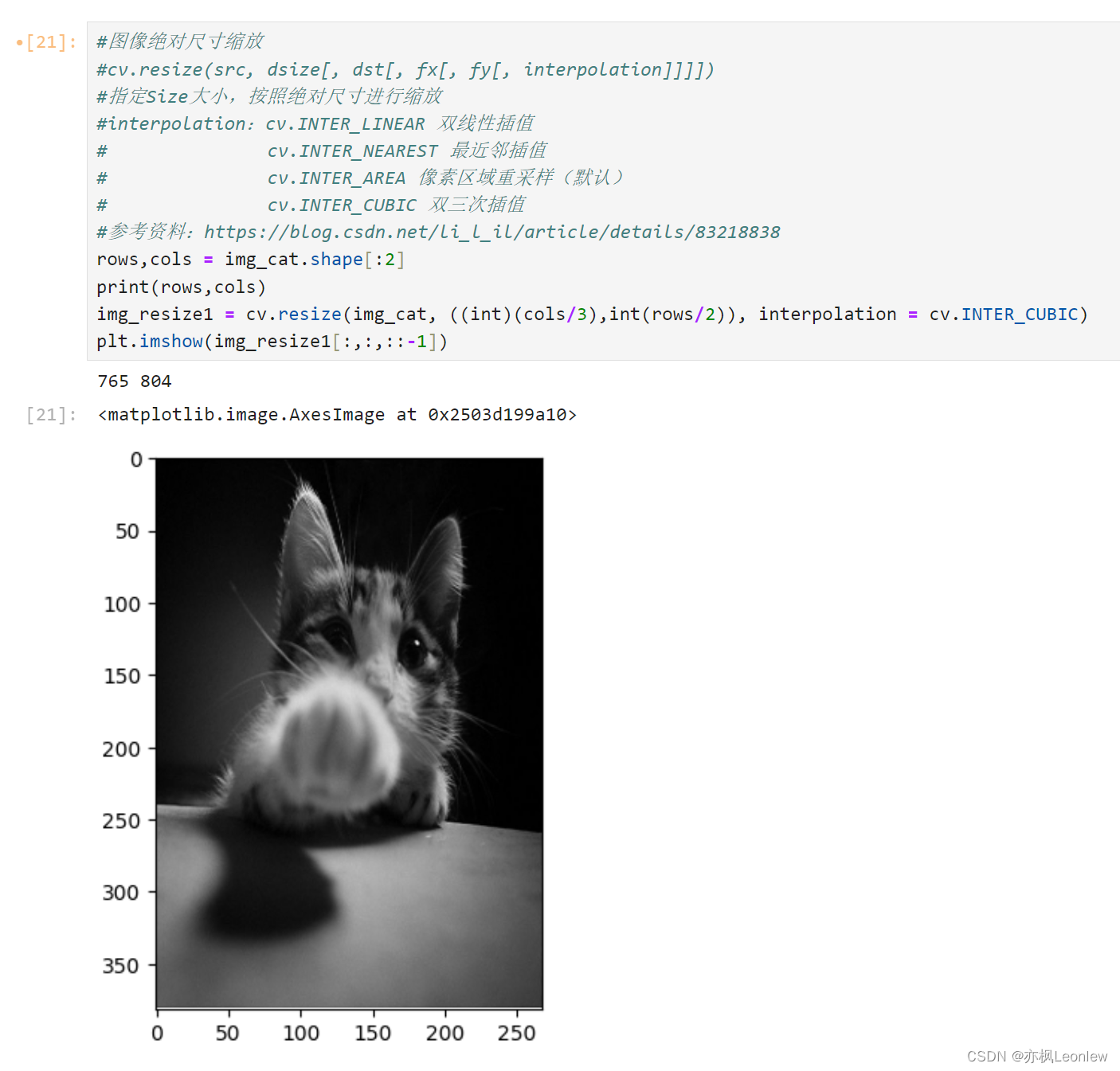
#图像绝对尺寸缩放
#cv.resize(src, dsize[, dst[, fx[, fy[, interpolation]]]])
#指定Size大小,按照绝对尺寸进行缩放
#interpolation:cv.INTER_LINEAR 双线性插值
# cv.INTER_NEAREST 最近邻插值
# cv.INTER_AREA 像素区域重采样(默认)
# cv.INTER_CUBIC 双三次插值
#参考资料:https://blog.csdn.net/li_l_il/article/details/83218838
rows,cols = img_cat.shape[:2]
print(rows,cols)
img_resize1 = cv.resize(img_cat, ((int)(cols/3),int(rows/2)), interpolation = cv.INTER_CUBIC)
plt.imshow(img_resize1[:,:,::-1])
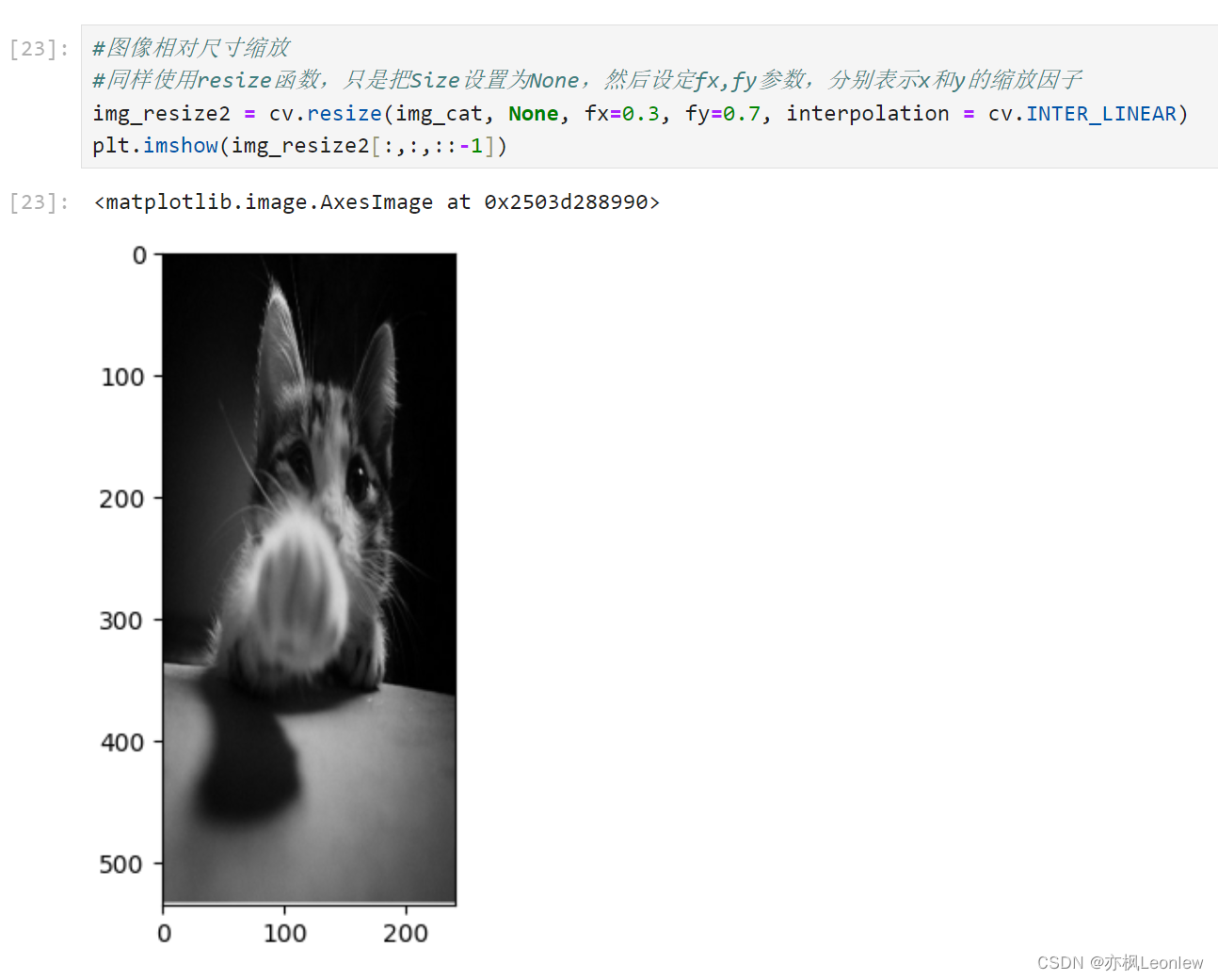
#图像相对尺寸缩放
#同样使用resize函数,只是把Size设置为None,然后设定fx,fy参数,分别表示x和y的缩放因子
img_resize2 = cv.resize(img_cat, None, fx=0.3, fy=0.7, interpolation = cv.INTER_LINEAR)
plt.imshow(img_resize2[:,:,::-1])