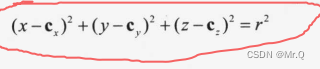日前价格预测
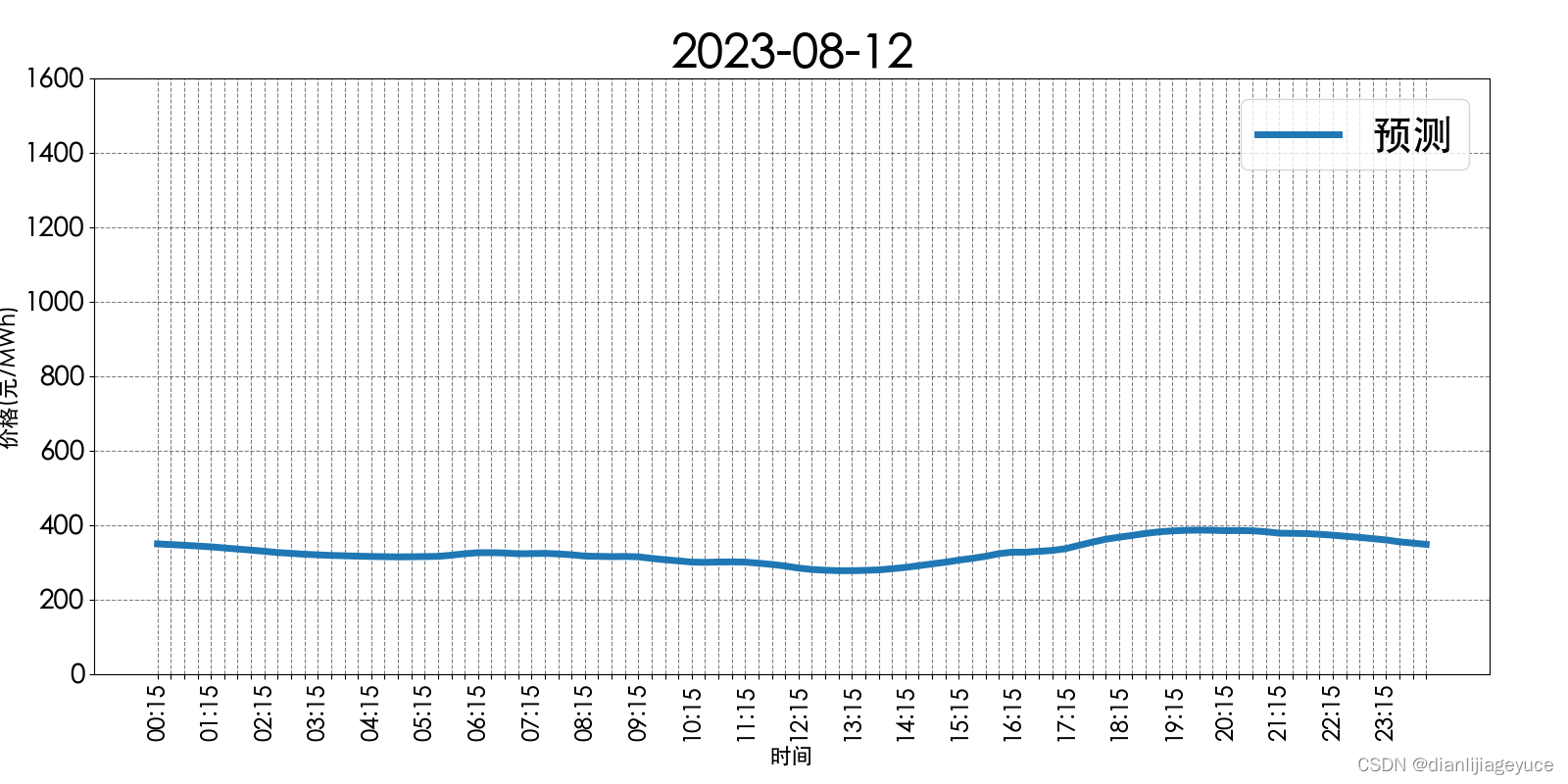
预测明日(2023-08-12)山西电力市场全天平均日前电价为330.52元/MWh。其中,最高日前电价为387.00元/MWh,预计出现在19: 45。最低日前电价为278.05元/MWh,预计出现在13: 00。
价差方向预测
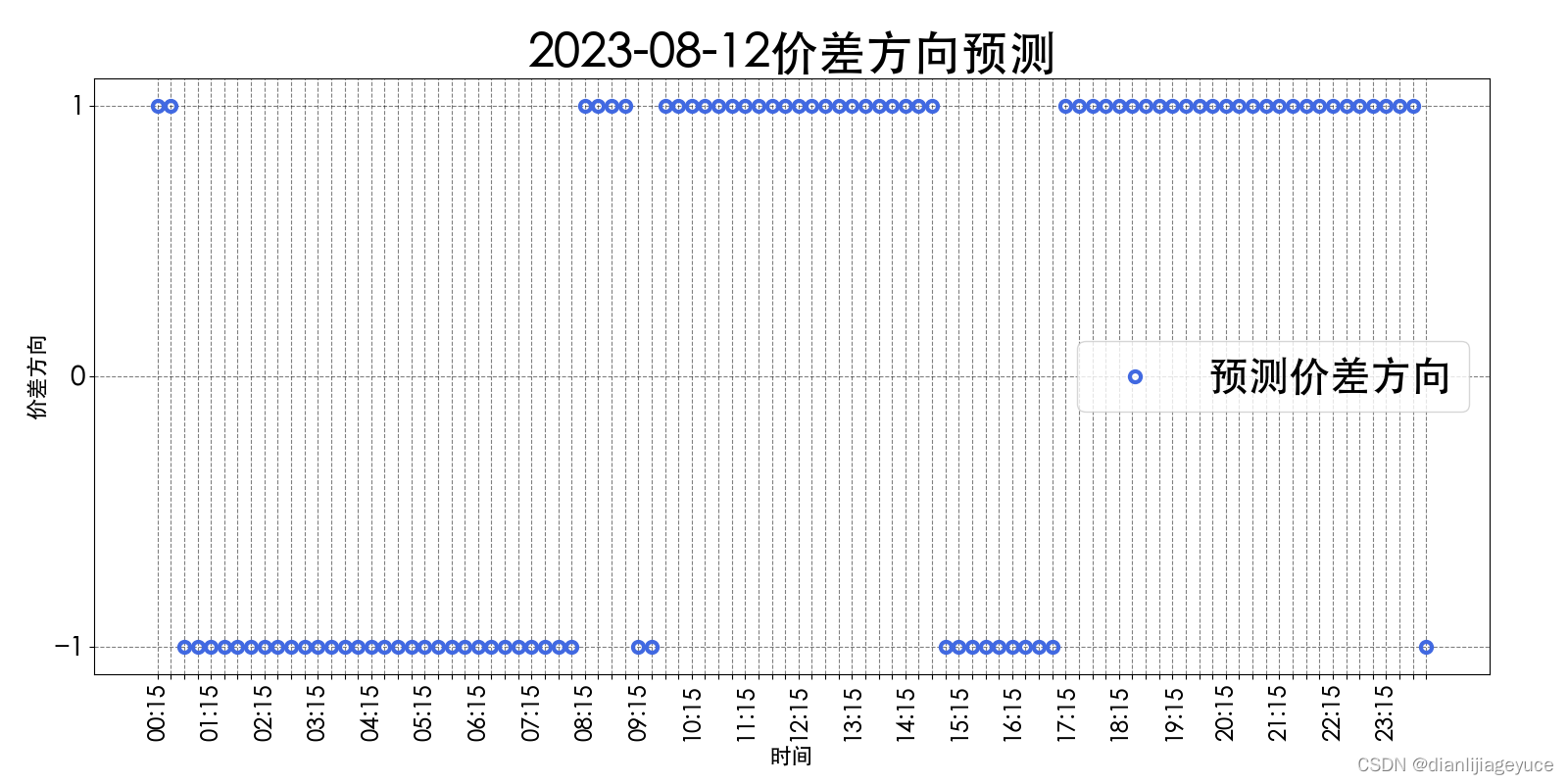
1: 实时价格 > 日前价格
0: 实时价格 = 日前价格
-1:实时价格 < 日前价格
注:价差代表的是原始出清价格的价差,并非最终结算价格的价差。
以上预测仅供学习参考,严禁用于商业用途。
昨日日前价格预测回顾
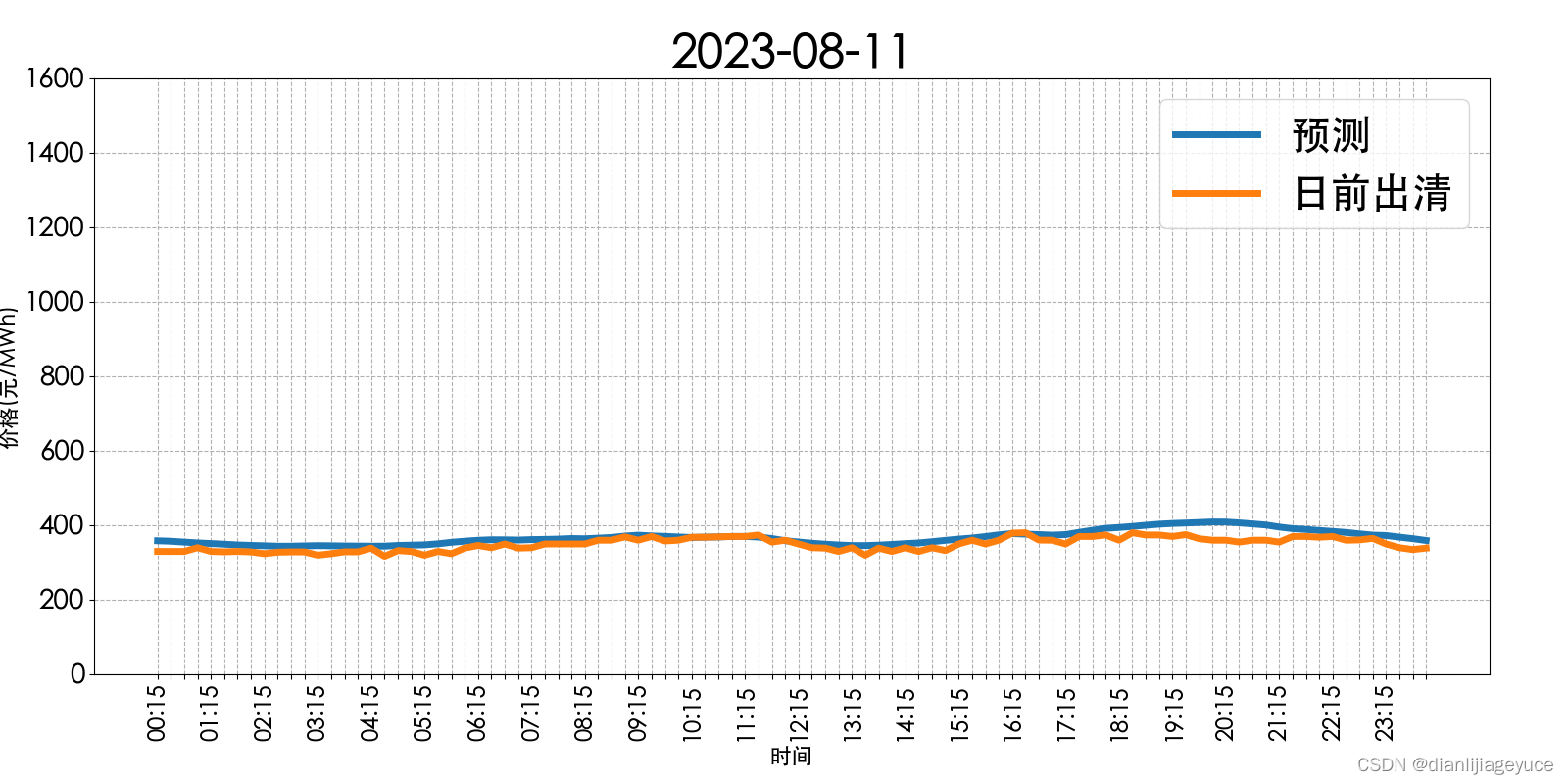
2023-08-11 全天96个点平均预测准确率94.85%,平均绝对偏差为17.99元/MWh。最大偏差为51.39元/MWh,出现在20:30。最小偏差为0.00元/MWh,出现在11:00。
价差方向预测回顾
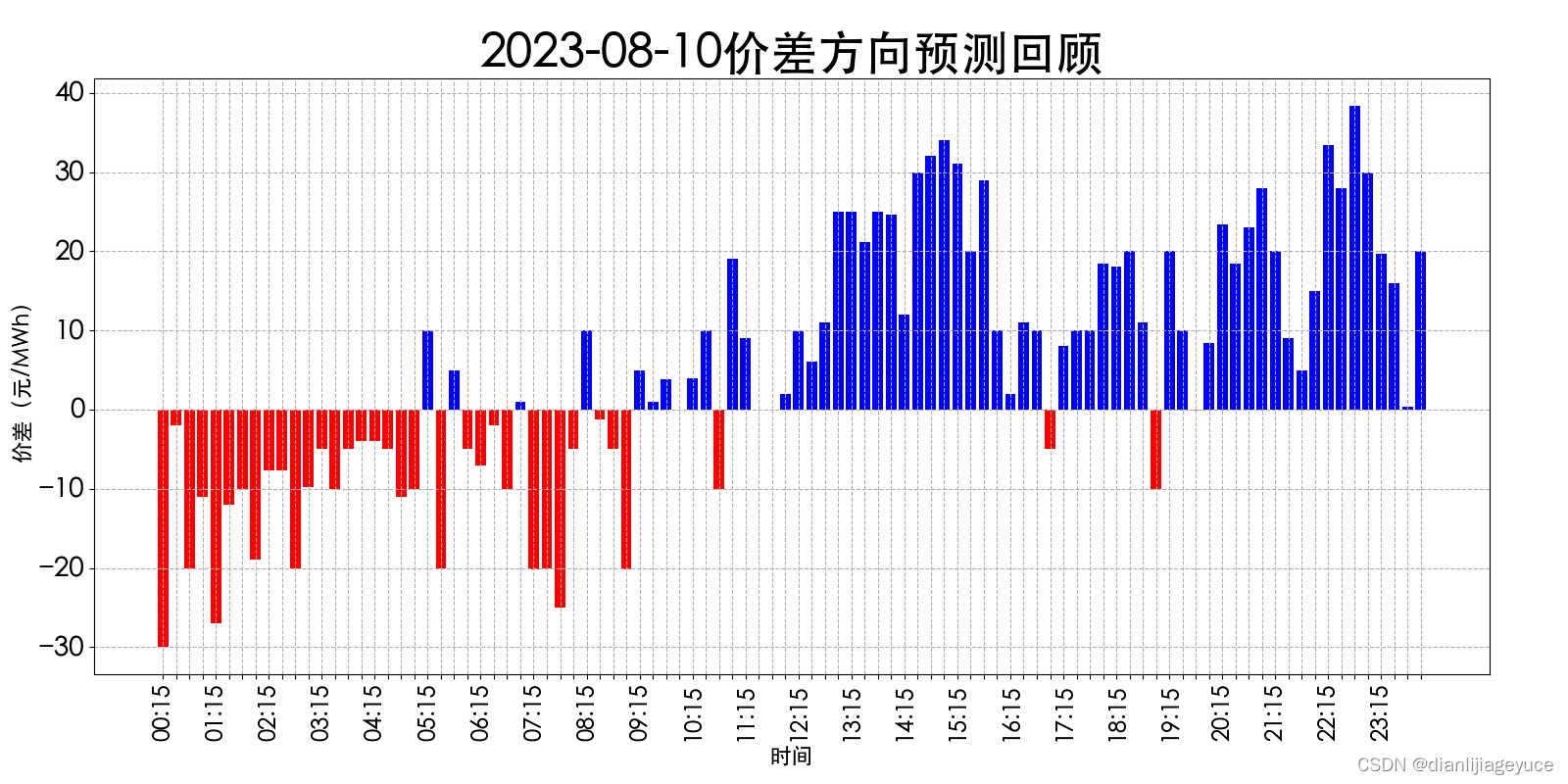
蓝色柱状图表示:该时段预测价差方向与实际价差方向一致。
红色柱状图表示:该时段预测价差方向与实际价差方向相反。
2023-08-10 全天96个时段价差方向预测准确率:39.4%
注:价差方向预测准确率计算公式:
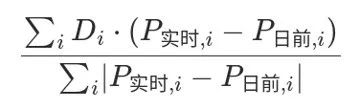
D:价差方向预测值(1:实时>日前,0:实时=日前,-1:实时<日前)
P: 价格
i: 时段