题目：

 题解思考：

这个题目我有两种解题方法：

1）利用数组，数组的下标。

2）利用等差数列的规律（这个可能比较难理解），行和列的递增规律。

注意输出格式的处理和多组输入。

数组解法

 数字递增的走向就是按箭头标注的走向。

 思路：

          可以发现第一排的走向是（0,0）

                        第二排的走向是（1,0）--->（0,1）

                        第三排的走向是（2,0）---->（1,1）---->（0,2）

      1） 上述可以发现横坐标每次移动的时候会-1，纵坐标每次移动的时候会+1

      2） 也可以知道每增加一排能得出结果的数字量=上一排的数字量+1，第一排的数字量为1

我们可以利用上面提到的特征，然后再用一个数来记录当前数的值，按上面的规律循环，再把这个数不断的+1，最后就能得到一个蛇形矩阵。

代码实现：

#include<stdio.h>
int n,x[101][101];
int main() {
	while(scanf("%d",&n)!=EOF) {
		int sum=1;
		for(int i=0; i<n; i++) {
			for(int j=0; j<=i; j++) {//i是每一排能得到的数字量，在外层for循环的影响下不断的+1
				x[i-j][j]=sum;//这里是横坐标不断的-1，纵坐标不断的+1
				sum++;//记录当前的数，不断的+1
			}
		}
		for(int i=0; i<n; i++) {//最后按照指定的格式输出
			for(int j=0; j<n-i; j++) {
				printf("%d ",x[i][j]);
			}
			printf("\n");
		}
	}
	return 0;
}

等差数列的规律解法

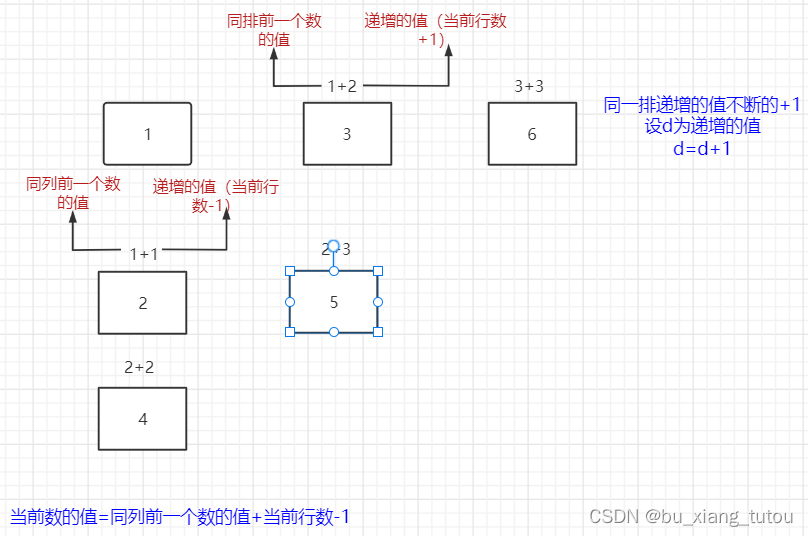
 要把行和列的递增分开来观察

行的递增规律：

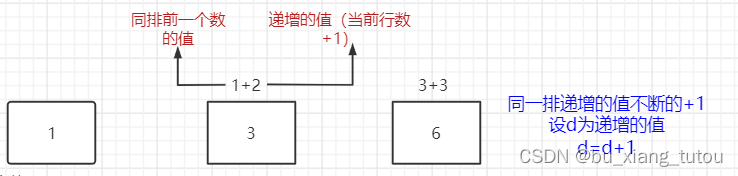
按照行的递增规律，我们需要一个数来记录同行上一个递增的值。然后不断的在这个基础上+1；

 

列的递增规律（特指第一列）：

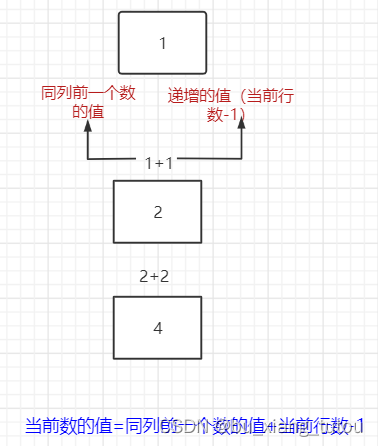
按照列的递增规律，我们需要一个数来记录同列上一个数的值，然后用这个数加上当前行数。

注意一下，这里的列的递增规律是特指的第一列。

 思路：

        1）需要一个数来记录当前行数（i）；

             一个数来记录当前一行的第一个数的值（a），然后a的值不断的递增输出；

             一个数来记录要不断递增的值（d）；

             一个数来记录上一行的第一个值（b）。

        2）按照总结出来的行与列的递增规律，来实现蛇形矩阵的输出。注意格式的处理。

代码实现：

#include<stdio.h>
int n;
int main(){
	while(scanf("%d",&n)!=EOF){
		int a,b,c,d;
		a=b=1;
		for(int i=1;i<=n;i++){
			a=b+i-1;//当前行的第一个数的值=上一行的第一个数的值+当前行数-1
			b=a;//记录上一行的第一个数的值
			d=i+1;//记录每一列的第一个递增的值，为当前行数+1
			for(int j=i;j<=n;j++){
				printf("%d",a);
				if(j==n){//格式的处理
					printf("\n");
				}else{
					printf(" ");
				}
				a=a+d;
				d++;//每一列递增的值，不断的+1
			}
		} 
	}
	return 0;
} 

 

最后再说一句，这个题目的解法多种多样，重要的是要理解思路。😊

不要copy代码哟😛！！！要理解思路！！👍