本文重点

本节课程我们学习使用学习曲线来判断某一个学习算法是否处于偏差、方差问题。学习曲线其实就是训练误差和验证误差关于样本m的曲线，我们将通过学习曲线来判断该算法是处于高偏差问题，还是处于高方差问题。

高偏差问题（欠拟合）

 

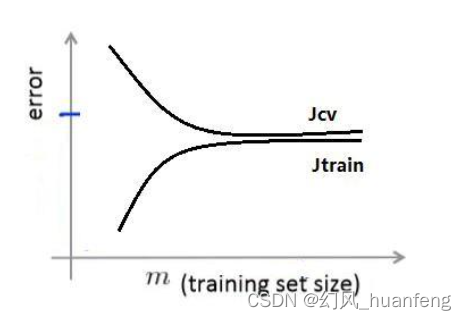
注意：这个m表示训练集数据样本数，其中训练误差是使用训练集算出来的，而验证集误差是使用验证集算出来的。因为不同的m求出的训练误差不同，因为梯度下降要最小化训练误差，那么此时的参数θ不同，那么验证集误差也不同，所以验证集误差也会随着训练集m而变化

 

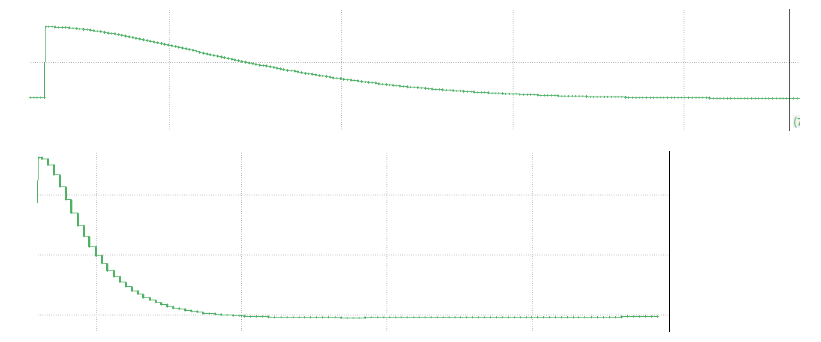
如欠拟合的学习曲线所示，当我们的训练数据很小的时候，泛化程度不会很好（验证集误差大），模型不能很好的适应新的样本，因此，此时不会是一个很好的假设。

随着训练集样本容量的增加，验证集误差和训练集误差都会而减少，所以当我们使用数据越多，越能获得更好的泛化表现，因此数据越多，越能拟合出合适的假设。

通过上面的图像，我们可以看出随着训练样本m的增加，我们的训练误差是越来越大的，而我们的交叉验证误差是越来越小的，这是一个趋势。

我们可以看到当我们的训练样本m增多的时候，此时训练误差和交叉验证误差会非