文章目录
- 一、局部变量
- 二、全局变量
一、局部变量
四种声明方式 + 多变量声明:
package main
import "fmt"
//局部变量声明
func main() {
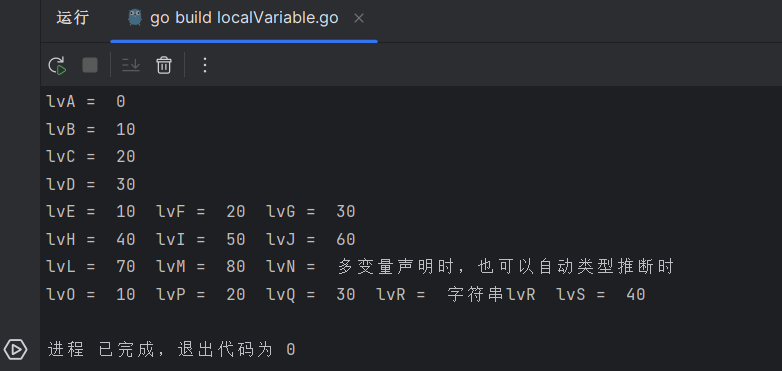
//方法一: 声明一个变量和数据类型,不初始化值;默认值为0;
var lvA int
fmt.Println("lvA = ", lvA)
//方法二: 声明一个变量和数据类型,并且初始化值。
var lvB int = 10
fmt.Println("lvB = ", lvB)
//方法三: 声明一个变量,不指定数据类型,但是初始化值;Golang 会自动推断设置这个变量的数据类型;
var lvC = 20
fmt.Println("lvC = ", lvC)
//方法四: 省略 var 关键字, 省略类型指定,使用 := 直接声明变量和初始化值。(常用方法) (但不支持这样声明全局变量)
lvD := 30
fmt.Println("lvD = ", lvD)
//多变量声明 方式一: 单行写法
//可以先一次声明多个,然后再一次单个或多个赋值
var lvE, lvF, lvG int
lvE = 10
lvF, lvG = 20, 30
fmt.Println("lvE = ", lvE, " lvF = ", lvF, " lvG = ", lvG)
//可以在声明多个变量的同时,初始化值
var lvH, lvI, lvJ int = 40, 50, 60
fmt.Println("lvH = ", lvH, " lvI = ", lvI, " lvJ = ", lvJ)
//可以同时声明多个不同类型的变量,根据初始化值,自动推断类型
var lvL, lvM, lvN = 70, 80, "多变量声明时,也可以自动类型推断时"
fmt.Println("lvL = ", lvL, " lvM = ", lvM, " lvN = ", lvN)
//多变量声明 方式二:多行写法
var (
//可以声明类型, 并初始化值 (多行时,必须要初始化值)
lvO int = 10
lvP = 20
lvQ, lvR = 30, "字符串lvR"
//也可以这样只声明但是不初始化值
//不过如果不初始化值,则必须指定类型,不然不知道这个变量的类型
lvS int
)
lvS = 40
fmt.Println("lvO = ", lvO, " lvP = ", lvP, " lvQ = ", lvQ, " lvR = ", lvR, " lvS = ", lvS)
}
二、全局变量
全局变量的声明和局部变量的声明方式一、二、三 相同;
但是不能使用局部变量声明方式四 (:=) 来声明全局变量。
package main
import "fmt"
//全局变量声明:和局部变量声明方法的一二三相同
var gvA int
var gvB int = 10
var gvC = 20
//不能使用 := 来声明全局变量,编译会报错
// gvD := 30
//全局变量的多个变量声明和局部变量一样
var gvL, gvM, gvN = 70, 80, "多变量声明时,也可以自动类型推断时"
var (
//可以声明类型, 并初始化值 (多行时,必须要初始化值)
gvO int = 10
gvP = 20
gvQ, gvR = 30, "字符串gvR"
//也可以这样只声明但是不初始化值
//不过如果不初始化值,则必须指定类型,不然不知道这个变量的类型
gvS int
)
func main() {
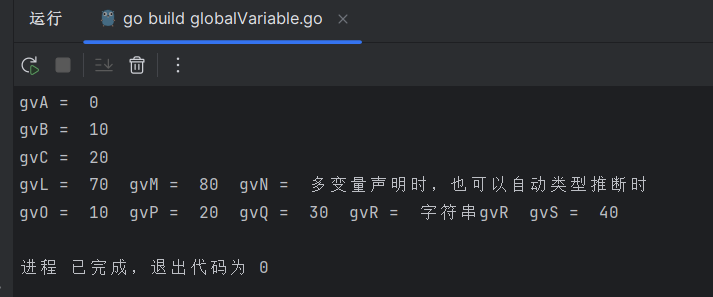
fmt.Println("gvA = ", gvA)
fmt.Println("gvB = ", gvB)
fmt.Println("gvC = ", gvC)
fmt.Println("gvL = ", gvL, " gvM = ", gvM, " gvN = ", gvN)
gvS = 40
fmt.Println("gvO = ", gvO, " gvP = ", gvP, " gvQ = ", gvQ, " gvR = ", gvR, " gvS = ", gvS)
}