202. 快乐数

202. 快乐数https://leetcode.cn/problems/happy-number/

题目：

编写一个算法来判断一个数 n 是不是快乐数。

「快乐数」 定义为：

对于一个正整数，每一次将该数替换为它每个位置上的数字的平方和。
然后重复这个过程直到这个数变为 1，也可能是 无限循环 但始终变不到 1。
如果这个过程 结果为 1，那么这个数就是快乐数。

如果 n 是 快乐数 就返回 true ；不是，则返回 false 。

解题思路：

我们先通过这两个测试用例来看看是什么情况

我们发现不管是19还是2都会形成一个环状结构（19的环状结构内都是1）

那这样我们就可以使用快慢指针来操作！！！

定义一个slow和fast，slow一次走一步，fast一次走两步

他们一定会相遇的，只不过相遇的时候会有两种情况，相遇的数是1或者不是1

那为什么一定会形成环状结构呢？我们来简单论证一下！

鸽巢原理：就是当n个巢穴，n+1个鸽子的时候，一定至少有一个巢穴的鸽子>1

我们注意一下n的范围，n最大为2的31次方，也就是2亿多（10位数）,那我们将它放大10个9（也就是最大的那个10位数，我懒得打9了），也就是说，它最多就是10个9，经过f操作最大就是9^2*10=810,也就是相当于我们最多有810个位置，我们处理813次的f，肯定会有重复的数出现！

那同理：

解题代码：

class Solution {
public:
    int f(int n)
    {
        int arr[11] = { 0 };
        int i = 1;
        for (int i = 1; i < 11; ++i)
        {
            if (n < 10)
            {
                arr[i] = n;
                break;
            }
            arr[i] = n % 10;
            n = n / 10;
        }
        int x = 0;
        for (int i = 1; i < 11; ++i)
        {
            x += (arr[i] * arr[i]);
        }
        return x;
    }
    bool isHappy(int n) {
        //快慢双指针
        int slow = n;
        int fast = n;
        //更新slow和fast
        slow = f(slow);
        fast = f(fast);
        fast = f(fast);
        if (slow == fast && slow == 1)return true;
        while (slow != fast)
        {
            //更新slow和fast
            slow = f(slow);
            fast = f(fast);
            fast = f(fast);
        }
        if (slow == 1)
            return true;
        else
            return false;
    }
};

11. 盛最多水的容器

11. 盛最多水的容器https://leetcode.cn/problems/container-with-most-water/

题目描述：

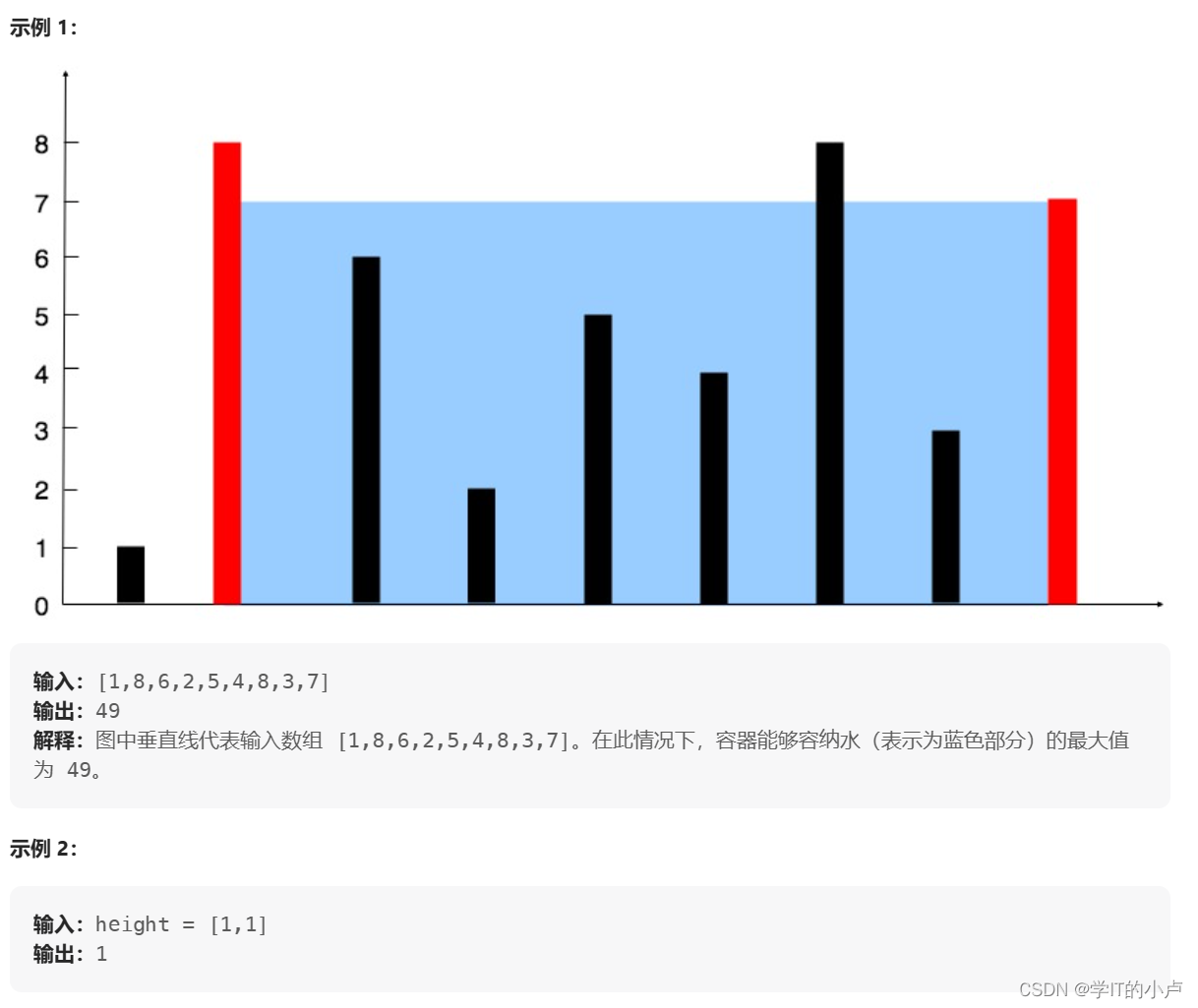
给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。

找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

返回容器可以储存的最大水量。

说明：你不能倾斜容器。

解题思路：

体积V=h*w,当我们利用双指针从左右两边向中间逼近，w一定是减小的，只有当h增大才可能增大

解题代码：

class Solution {
public:
    int maxArea(vector<int>& height) {
        int left=0;
        int right=height.size()-1;
        int ret=0;
        while(left<right)
        {
            int v=min(height[left],height[right])*(right-left);
            ret=max(v,ret);
            if(height[left] < height[right]) left++;
            else right--; 
        }
        return ret;
    }
};