2023河南萌新联赛第（五）场：郑州轻工业大学-F 布鲁特佛斯

https://ac.nowcoder.com/acm/contest/62977/F

题意

给定一个边长为$n(2\le n\le 1000)$的正方形方框，以及无数个边长为$2\sim 50$ 的正方形拼图, 请求出恰好填满这个正方形方框的任意合法方案；若不存在构造方案，请输出$-1$。

下图是填满边长为$112$的正方形边框的一种可能构造方式：

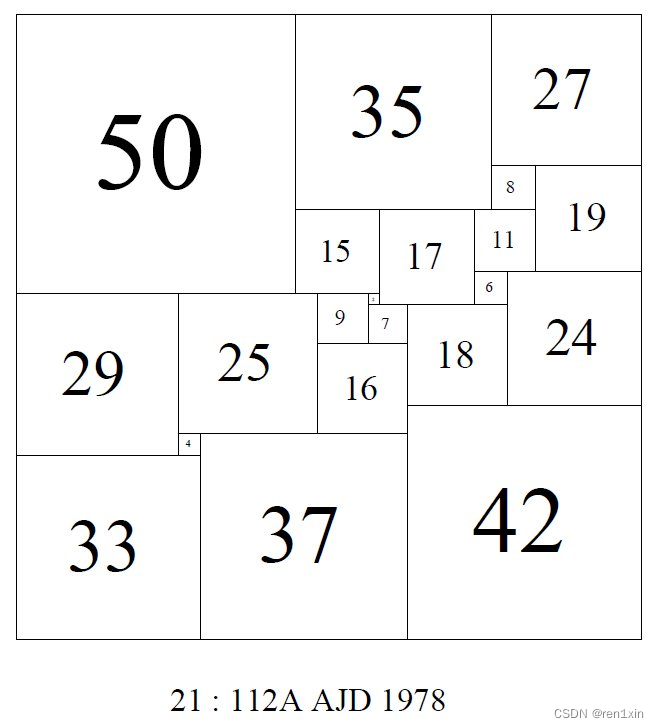
请注意，尽管拼图是无限的，但最终构造方案使用的正方形拼图个数应该小于$10^6$

解题思路

最后一句是废话，无论怎么构造都不会超过$10^6$。

该题有多种构造方法，下面是出题人给的一种：
对于$n\le 50$则直接用一个正方形填充，对于$n$为偶数，可以用边长为$2$的小正方形填充，对于其他情况，可以按如下图：

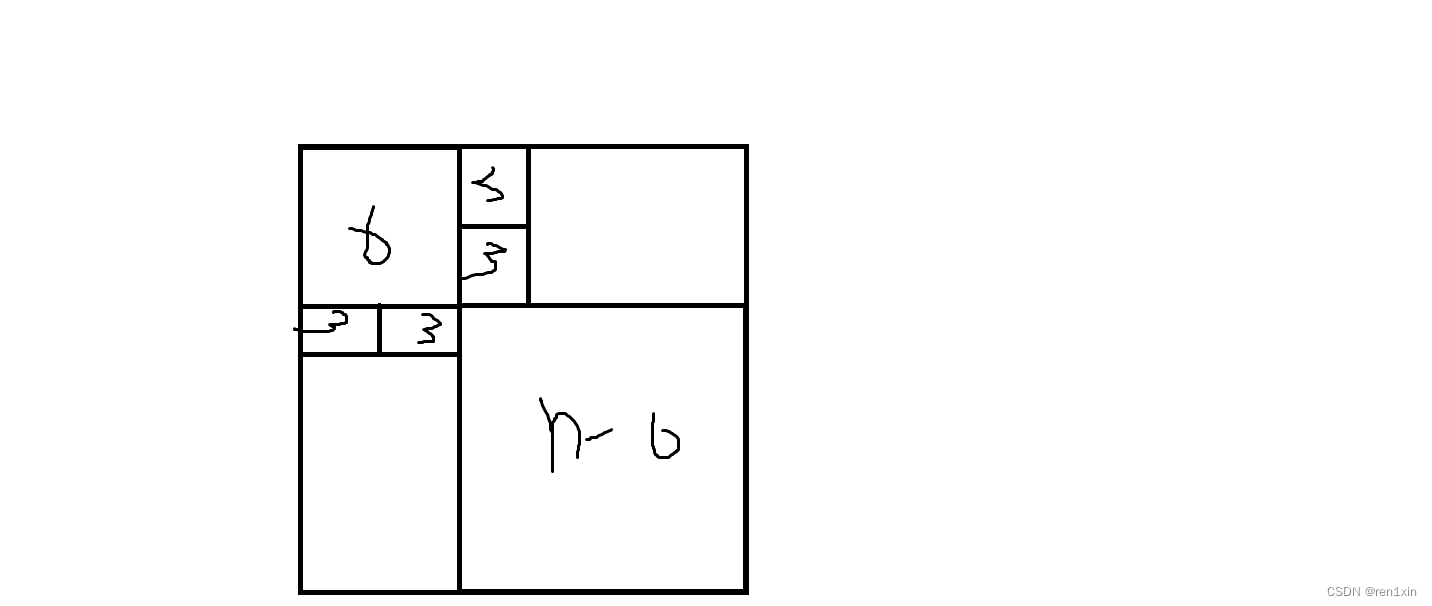
对于左下角与右上角的长方形，长为$n-9$，宽为$6$，由于$n$为奇数，所以$n-9$也是奇数，可以直接用边长为$2$的正方形填充，然后递归$n-6$的长方形，仍然按上述方法填充，知道剩下边长$\le 50$时，结束。

代码

#include<bits/stdc++.h>
#define ll long long
using namespace std;
int n;
struct node{
    int x,y,z;
};
vector<node>a;
int x[1000]={0,1,1,4,7,7},y[1000]={0,1,7,7,1,4},z[1000]={0,6,3,3,3,3},cnt=5;
void dfs(int p,int q){
    if(n-p+1<=50){
        a.push_back(node{p,q,n-p+1});
        return;
    }
	for(int i=1;i<=cnt;i++)a.push_back(node{x[i]+p-1,y[i]+q-1,z[i]});
    for(int i=p+9;i<=n;i+=2)
        for(int j=q;j<q+6;j+=2)
            a.push_back(node{i,j,2}),a.push_back(node{j,i,2});
    dfs(p+6,q+6);
}
int main(){
	cin>>n;
	if(n<=50){
		cout<<"1\n";
		cout<<"1 1 "<<n;
		return 0;
	}
	if(n%2==0){
		cout<<n*n/4<<'\n';
		for(int i=1;i<=n;i+=2){
			for(int j=1;j<=n;j+=2){
				cout<<i<<' '<<j<<' '<<2<<'\n';
			}
		}
		return 0;
	}
    dfs(1,1);
    cout<<a.size()<<'\n';
    for(auto b:a){
        cout<<b.x<<' '<<b.y<<' '<<b.z<<'\n';
    }
}