JDK安装
https://www.oracle.com/java/technologies/downloads/
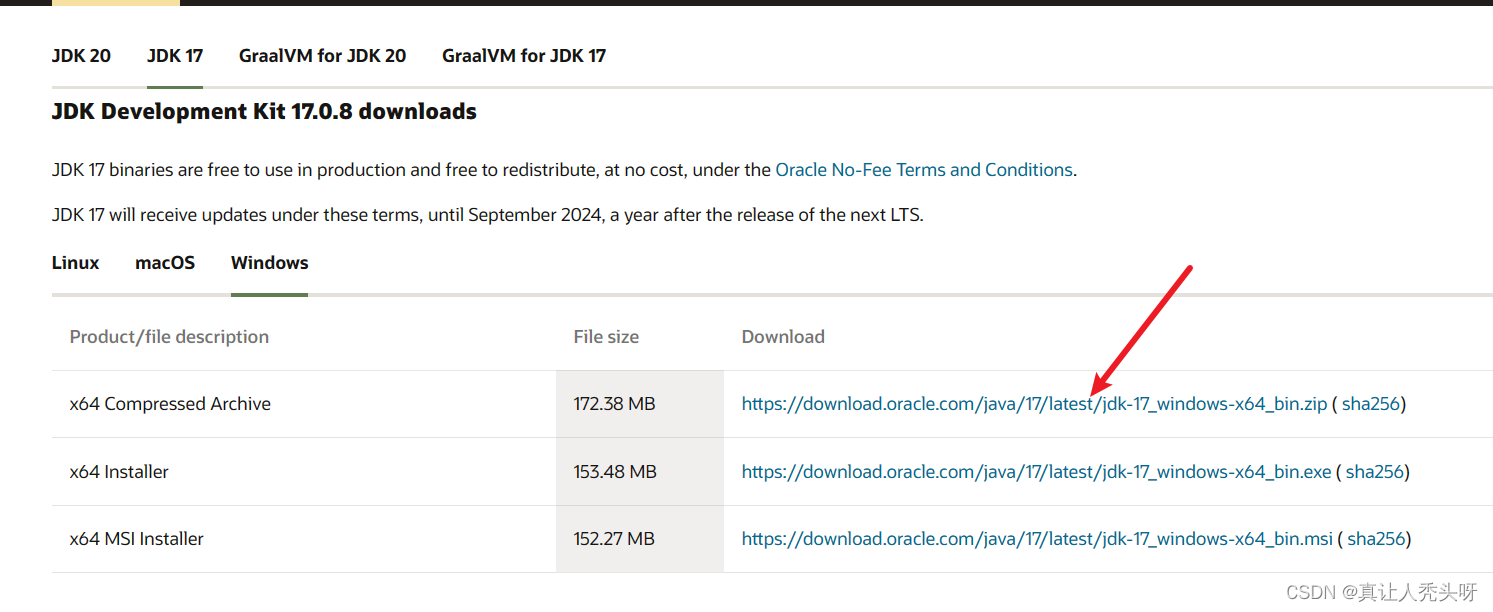
安装完成后,一直点下一步就行
打开控制面板输入cmd运行,控制台输入java -version。如果看到版本号就说明我们安装成功了

JDK的组成
1. JVM
JAVA虚拟机,JAVA真正运行的地方
2. 核心类库
JAVA内置的程序, 给程序员调用
3. JRE
JAVA运行环境
安装IDEA
https://www.jetbrains.com/zh-cn/idea/download/?section=windows
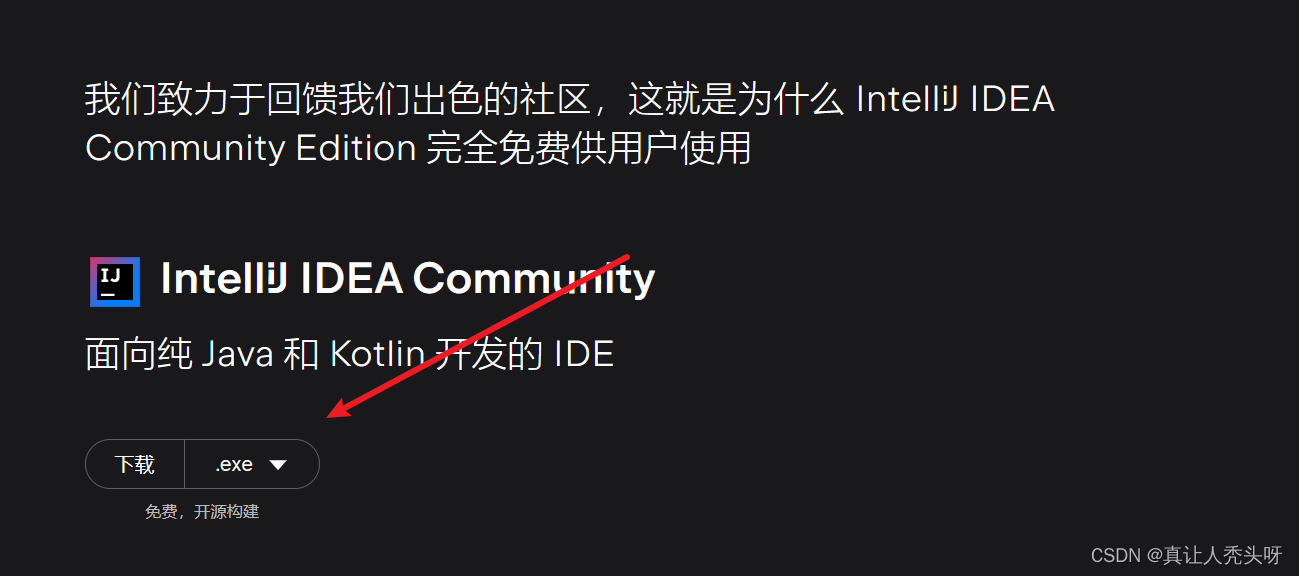
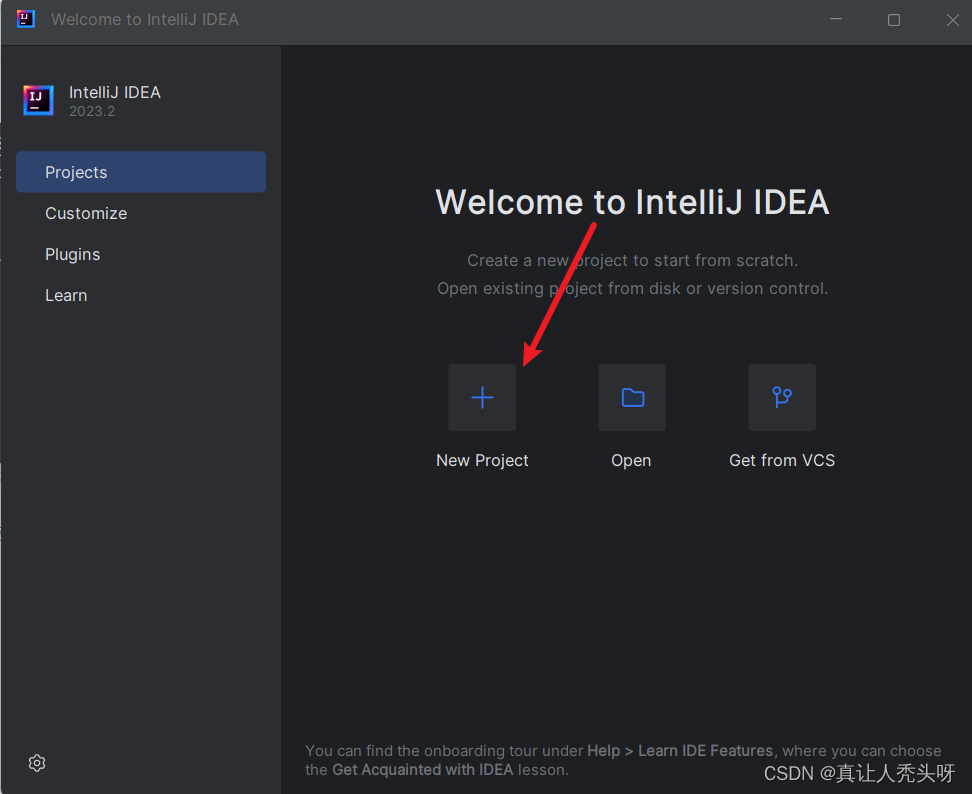
安装完成后,一直点下一步就行。安装完成后打开idea选择新建项目
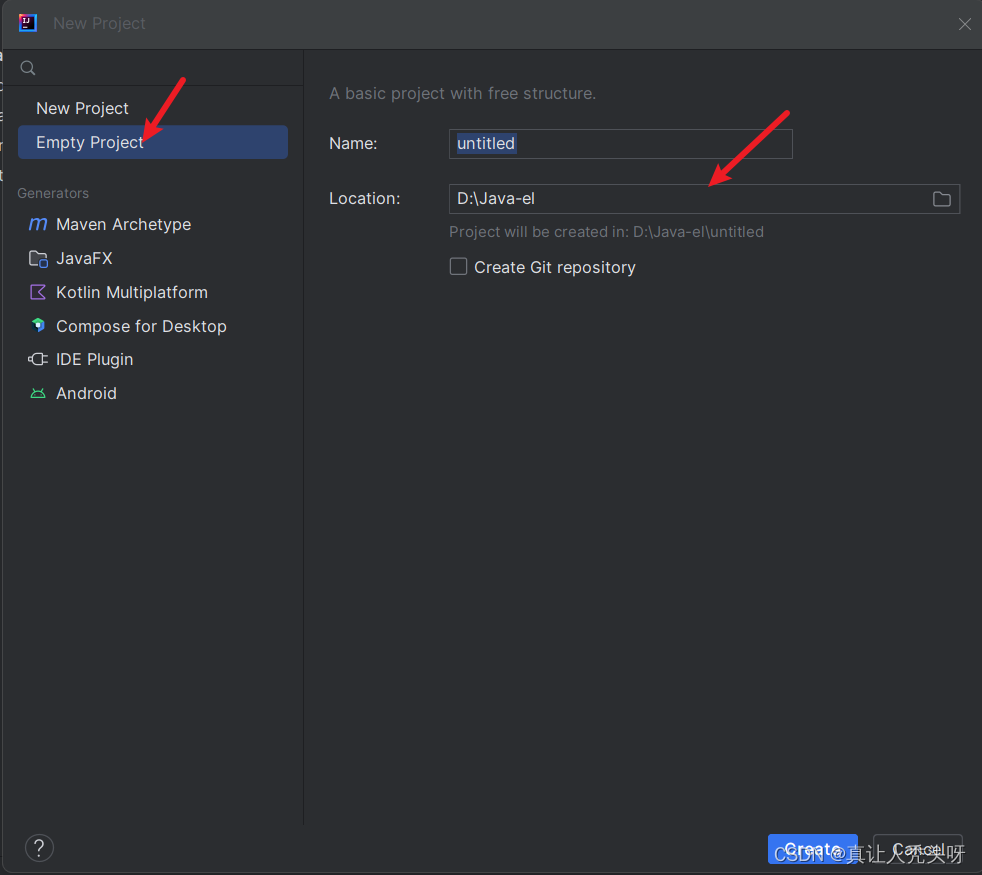
下面选择一个空目录,然后创建项目路径点击创建
进入项目后右键创建一个class文件
输入如下代码点击运行。如何看到控制台打印hello world就说明我们成功了。下面可以开启java之旅了



![[保研/考研机试] KY110 Prime Number 上海交通大学复试上机题 C++实现](https://img-blog.csdnimg.cn/fa301eee29874196802379554e278ba4.png)