1 引言

在前面的文章中已经介绍了一系列激活函数 (Sigmoid、Tanh、ReLU、Leaky ReLU、PReLU、Swish、ELU、SELU、GELU、Softmax、Softplus、Mish、Maxout、HardSigmoid、HardTanh、Hardswish)。在这篇文章中，会接着上文提到的众多激活函数继续进行介绍，给大家带来更多不常见的激活函数的介绍。这里放一张激活函数的机理图：

最后，对于文章中没有提及到的激活函数，大家可以通过评论指出，作者会在后续的文章中进行添加补充。

2 激活函数

2.1 HardShrink激活函数

HardShrink激活函数的数学表达式和数学图像分别如下所示：
$$HardShrink(x)=\{\begin{array}{c}xifx>+threshold\\ xifx<-threshold\\ 0otherwise\end{array}$$
上面这幅图像是连续的（这是因为以直线的形式画出来了，会将断点连接），实际上的图像是非连续的，如下所示：

其中，$threshold$ 是硬缩减的阈值，通常为一个预先设定的常数。

优点：

• 硬缩减：HardShrink激活函数在输入值小于阈值时直接将输出缩减为0，从而引入了非线性变换。这种硬缩减操作可以帮助模型学习具有稀疏性的表示，有助于减少模型的计算复杂性和参数数量。
• 无需学习参数：HardShrink激活函数不需要学习任何参数，因为它只是简单地对输入进行硬缩减。这使得HardShrink函数非常轻量级，适用于一些资源有限的场景和轻量级模型。

缺点：

• 硬缩减的信息丢失：HardShrink函数在阈值区间时直接将输出设为0，这可能导致部分信息的丢失。因此，HardShrink函数可能不适用于一些需要保留全部信息的任务。
• 不连续性：HardShrink函数在阈值处存在不连续性，这意味着在这些点上梯度不连续。这可能会影响梯度优化过程的稳定性和收敛性。
• 参数选择：HardShrink激活函数的性能高度依赖于阈值的选择。选择不合适的阈值可能导致性能下降，因此需要进行一定的调参。

对于不连续的HardShrink激活函数，几乎没有人使用。。。

2.2 SoftShrink激活函数

SoftShrink激活函数的数学表达式和数学图像分别如下所示：
$$SoftShrink(x)=\{\begin{array}{c}x-thresholdifx>+threshold\\ x+thresholdifx<-threshold\\ 0otherwise\end{array}$$

与HardShrink激活函数相比，SoftShrink激活函数是连续的，具有更少的稀疏性，保存更多的信息。同时，由于其连续性，在进行优化时过程会更加稳定。

SoftShrink在一定程度上改善了HardShrink的情况，但是在当前情况下仍不怎么使用。。。

2.3 TanhShrink激活函数

基于Tanh之上，计算输入输出的差值，即为TanhShrink。数学表达式和数学图像分别如下所示：
$$TanhShrink(x)=x-\tanh (x)=x-\frac{\exp (x)-\exp (-x)}{\exp (x)+\exp (-x)}=x_i-\frac{\exp (2x)-1}{\exp (2x)+1}$$

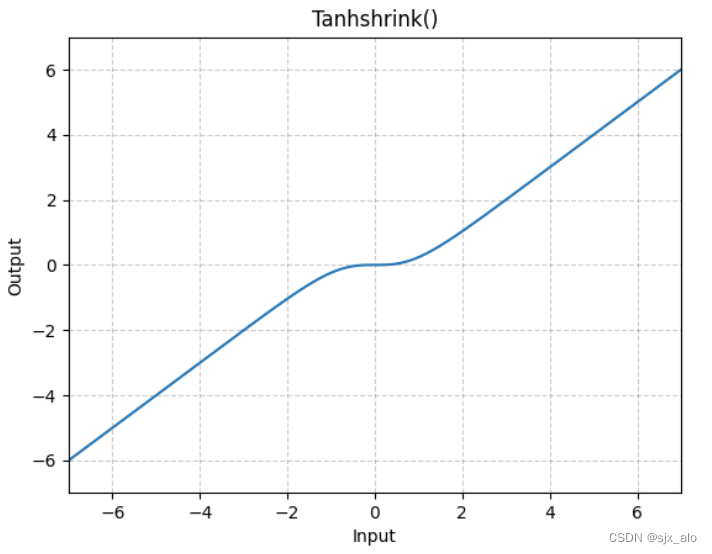
在当输入在0附近时，梯度近乎为0，而在输入极大或极小时，梯度反而为正常梯度。

TanhShrink相对于SoftShrink函数又具有一定的平滑性能，但是仍具有局限性（更多的是用作Tanh激活函数的代替）。。。

3. 总结

上述介绍的Shrink系列激活函数更多的是对Tanh函数的改进，同样地，这些函数也更适用于对Tanh函数进行替换，别的情况下很难得到应用。。。。
到此，使用 激活函数总结（五） 已经介绍完毕了！！！ 如果有什么疑问欢迎在评论区提出，对于共性问题可能会后续添加到文章介绍中。如果存在没有提及的激活函数也可以在评论区提出，后续会对其进行添加！！！！

如果觉得这篇文章对你有用，记得点赞、收藏并分享给你的小伙伴们哦😄。