题一：旋转数组

给定一个整数数组 nums，将数组中的元素向右轮转 k 个位置，其中 k 是非负数。 

思路一：

创建reverse()函数传入三个值分别为数组地址，从第几个数组元素开始，结束元素位置；

在reverse（）函数中实现颠倒，swap()函数实现交换。

先将数组分为两部分0--(k-1)和k--(sz-1),然后分别旋转；

//交换位置
void swap(int* a, int* b) {
    int t = *a;
    *a = *b, *b = t;
}
//实现颠倒
void reverse(int* nums, int start, int end) {
    while (start < end) {
        swap(&nums[start], &nums[end]);
        start += 1;
        end -= 1;
    }
}
//起始位置
void rotate(int* nums, int numsSize, int k)
{
    int sz = numsSize;
    int i = 0;
    int j = 0;
    int tmp = 0;
    k = k % sz;
    reverse(nums,0,sz-1);
    reverse(nums,0,k-1);
    reverse(nums,k,sz-1);

}

思路二：

如图：

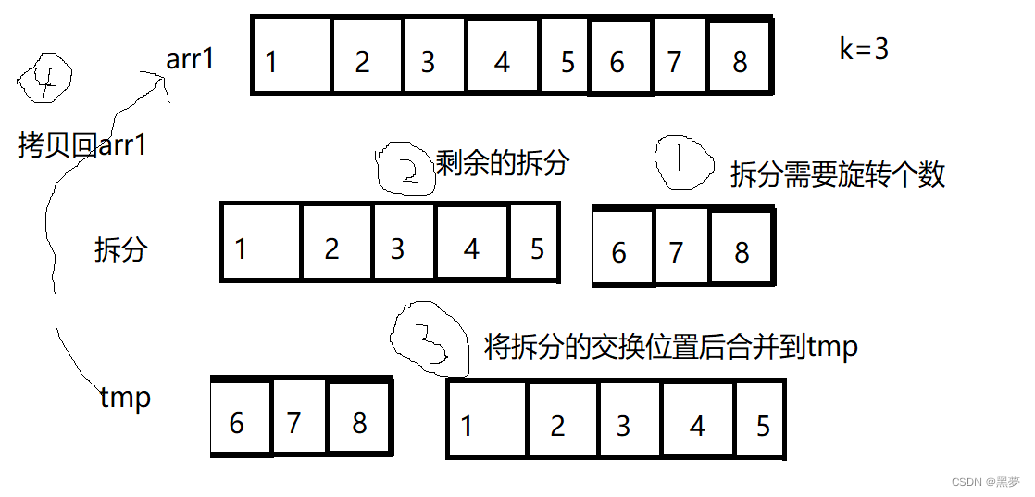
void rotate(int* nums, int numsSize, int k)
{
	int* tmp = (int*)malloc(sizeof(int) * numsSize);
	k = numsSize % k;
	
	memcpy(tmp, nums + numsSize - k, sizeof(int) * k);
	memcpy(tmp+k, nums, sizeof(int) * (numsSize - k));
	memcpy(nums, tmp , sizeof(int) * numsSize);
}

题二：消失的数字

数组nums包含从0到n的所有整数，但其中缺了一个。请编写代码找出那个缺失的整数。你有办法在O(n)时间内完成吗？

思路一：

将0--n的数全部加起来，然后减去数组中的值，最后得到的结果就是消失的数。

int missNumber(int* nums, int numsSize)
{
	int N = numsSize;
	int ret = N * (N + 1) / 2;
	for (int i = 0; i < N; i++)
	{
		ret -= nums[i];
	}
	return ret;
}

思路二：

单身狗问题解法：异或“ ^ ”

时间复杂度：O(N)

解法：定义一个数tmp为0，与0--n的数进行异或，然后与题所给的数组进行再次异或，

得出消失的数；

基础：a^a=0;a^b^a=b;

int missingNumber(int* nums, int numsSize)
{
    int n = numsSize;
    int i = 0;
    int tmp = 0;
    for(i = 0; i <= n;i++ )
    {
        tmp ^= i;
    }
    for(i = 0;i < n;i++)
    {
        tmp ^= nums[i];
    }
    return tmp;
}

题三：移除元素

给你一个数组 nums 和一个值 val，你需要 原地 移除所有数值等于 val 的元素，并返回移除后数组的新长度。

不要使用额外的数组空间，你必须仅使用 O(1) 额外空间并 原地 修改输入数组。

元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。

// nums 是以“引用”方式传递的。也就是说，不对实参作任何拷贝
int len = removeElement(nums, val);

// 在函数里修改输入数组对于调用者是可见的。
// 根据你的函数返回的长度, 它会打印出数组中 该长度范围内 的所有元素。
for (int i = 0; i < len; i++) {
    print(nums[i]);
}

思路一：

    解题思路：
        1. 从前往后遍历nums，找到val第一次出现的位置
        2. 将val之后的所有元素整体往前搬移，即删除该val
        3. nums中有效元素个数减少一个
    循环进行上述操作，直到nums中所有值为val的元素全部删除完
    时间复杂度:O(N^2)  空间复杂度:O(1)

int removeElement(int* nums, int numsSize, int val) {
    // 
    while (1)
    {
        // 1. 在nums中找val出现的位置
        int pos = 0;
        for (; pos < numsSize; ++pos)
        {
            if (nums[pos] == val)
            {
                break;
            }
        }


        // 2. 检测是否找到
        if (pos == numsSize)
            break;


        // 3. 找到值为value的元素--将其删除
        for (int j = pos + 1; j < numsSize; ++j)
        {
            nums[j - 1] = nums[j];
        }


        numsSize--;
    }


    return numsSize;
}

思路二：

    解题思路:
    因为题目说了，数组中元素个数最大为100，所以不用动态申请，至二级创建100个元素数组即可
        1. 创建一个100个元素的整形数组temp
        2. 遍历nums，将nums中所有与val不同的元素搬移到temp中
        3. 将temp中所有元素拷贝回nums中
       时间复杂度: O(N)  空间复杂度: O(N)

int removeElement(int* nums, int numsSize, int val) {
    // 1. 申请numSize个元素的新空间
    int temp[100];


    // 2. 将nums中非value的元素搬移到temp中---尾插到temp中
    int count = 0;
    for (int i = 0; i < numsSize; ++i)
    {
        if (nums[i] != val)
        {
            temp[count] = nums[i];
            ++count;
        }
    }


    // 3. 将temp中删除val之后的所有元素拷贝到nums中
    memcpy(nums, temp, sizeof(int) * count);
    return count;
}

思路三：

    解题思路:
        1. 设置一个变量count，用来记录nums中值等于val的元素的个数
        2. 遍历nums数组，对于每个元素进行如下操作：
            a. 如果num[i]等于val，说明值为val的元素出现了一次，count++
            b. 如果nums[i]不等于元素，将nums[i]往前搬移count个位置
                因为nums[i]元素之前出现过count个值等于val的元素，已经被删除了
                因此次数需要将nums[i]往前搬移
        3. 返回删除之后新数组中有效元素个数

    时间复杂度：O(N)   空间复杂度：O(1)

int removeElement(int* nums, int numsSize, int val) {
    int count = 0;
    for (int i = 0; i < numsSize; ++i)
    {
        if (nums[i] == val)
        {
            count++;
        }
        else
        {
            nums[i - count] = nums[i];
        }
    }


    return numsSize - count;
}

做错的选择题：

分析以下函数的时间复杂度

void fun(int n) {
  int i=l;
  while(i<=n)
    i=i*2;
}

A.O(n)

B.O(n^2)

C.O(nlogn)

D.O(logn)

答案：D

解析: 此函数有一个循环，但是循环没有被执行n次，i每次都是2倍进行递增，所以循环只会被执行log2(n)次。

给定一个整数sum，从有N个有序元素的数组中寻找元素a，b，使得a+b的结果最接近sum，最快的平均时间复杂度是（   ）

A.O(n)

B.O(n^2)

C.O(nlogn)

D.O(logn)

答案：A

  解析：此题目中，数组元素有序，所以a,b两个数可以分别从开始和结尾处开始搜，根据首尾元素的和是否大于sum,决定搜索的移动，整个数组被搜索一遍，就可以得到结果，所以最好时间复杂度为n

分析以下函数的空间复杂度（   ）

  int** fun(int n) {
    int ** s = (int **)malloc(n * sizeof(int *));
    while(n--)
      s[n] = (int *)malloc(n * sizeof(int));
    return s;
  }

A.O(n)

B.O(n^2)

C.O( 1 )

D.O(nlogn)

 解析：此处开辟的是一个二维数组，数组有n行，每行分别有1,2,3,...n列，所以是n(n + 1)/2个元素空间，空间复杂度为n^2