蜜蜂路线
题目背景
无
题目描述
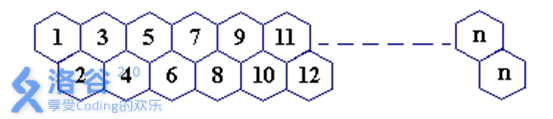
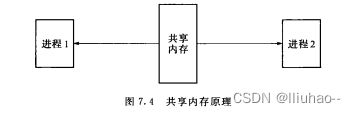
一只蜜蜂在下图所示的数字蜂房上爬动,已知它只能从标号小的蜂房爬到标号大的相邻蜂房,现在问你:蜜蜂从蜂房 m 开始爬到蜂房 n,m<n,有多少种爬行路线?(备注:题面有误,右上角应为n−1)
输入格式
输入m,n的值
输出格式
爬行有多少种路线
样例 #1
样例输入 #1
```
1 14
```### 样例输出 #1
```
377
```## 提示
对于100%的数据,1 <= M,N <= 1000
明显的斐波那契数列,因为第M号蜂巢只能从M-1号和M-2号来。
注意N,M可能达到1000,所以要高精度
#include <bits/stdc++.h>
using namespace std;
int m , n;
string f[1010] = {"0" , "1" , "1"};
string add(string A , string B){
int a[10010] , b[10010] , c[10010];
string r;
for ( int i = A.size()-1 ; i >= 0 ; i-- )
a[A.size()-i-1] = A[i] - '0';
for ( int i = B.size()-1 ; i >= 0 ; i-- )
b[B.size()-i-1] = B[i] - '0';
int len = max(A.size() , B.size());
int tmp=0;
for ( int i = 0 ; i <= len ; i++ ){
c[i] = a[i]+b[i]+tmp;
tmp = c[i] / 10;
c[i] %= 10;
}
if ( tmp != 0 )
c[++len] = tmp;
while ( c[len] == 0 )
len--;
for ( int i = len ; i >= 0 ; i-- )
r.push_back(c[i]+'0');
return r;
}
int main(){
scanf("%d%d" , &m , &n);
for ( int i = 3 ; i <= n - m + 1 ; i++ )
f[i] = add(f[i-1] , f[i-2]);
cout << f[n-m+1];
return 0;
}