基本动态规划问题的扩展
应用动态规划可以有效的解决许多问题,其中有许多问题的数学模型,尤其对一些自从57年就开始研究的基本问题所应用的数学模型,都十分精巧。有关这些问题的解法,我们甚至可以视为标准——也就是最优的解法。不过随着问题规模的扩大化,有些模型显出了自身的不足和缺陷。这样,我们就需要进一步优化和改造这些模型。
- 程序上的优化:
程序上的优化主要依赖问题的特殊性。我们以f(XT)= opt{f(uT)}+ A(XT), uTÎ Pred_Set(XT)这样的递推方程式为例(其中A(XT)为一个关于XT的确定函数,Pred_Set(XT)表示XT的前趋集)。我们设状态变量XT的维数为t,每个XT与前趋中有e维改变,则我们可以通过方程简单的得到一个时间复杂度为O(nt+e)的算法。
当然,这样的算法并不是最好的算法。为了简化问题,得到一个更好的算法。我们设每个XT所对应的g(XT)=opt{f(uT)},则f(XT)=g(XT)+A(XT),问题就变为求g(XT)的值。下面分两个方面讨论这个问题:
-
-
-
- Pred_Set(XT)为连续集:
-
-
在这样的情况下,我们可以用g(XT)= opt{g(Pred(XT)), f(Pred(XT))}这样一个方程式来求出g(XT)的值,并再用g(XT)的值求出f(XT)的值。这样,虽然我们相当于对g(XT)和f(XT)分别作了一次动态规划,但由于两个规划是同时进行的,时间复杂度却降为了O(nt)。由于我们在实际使用中的前趋即通常都是连续的,故这个方法有很多应用。例如IOI’99的《小花店》一题就可以用该方法把表面上的时间复杂度O(FV2)降为O(FV)。
-
-
-
- Pred_Set(XT)为与XT有关的集合:
-
-
这样的问题比较复杂,我们以最长不下降子序列问题为例。规划方程为:f(i)=max{f(j)}+1, d[i]≥ d[j]; i>j。通常认为,这个问题的最低可行时间复杂度为O(n2)。不过,这个问题只多了一个d[i]≥d[j]的限制,是不是也可以优化呢?我们注意到max{f(j)}的部分,它的时间复杂度为O(n)。但对于这样的式子,我们通常都可以用一个优先队列来使这个max运算的时间复杂度降至O(log n)。对于该问题,我们也可以用这样的方法。在计算d[i]时,我们要先有一个平衡排序二叉树(例如红黑树)对d[1]~d[i-1]进行排序。并且我们在树的每一个节点新增一个MAX域记录它的左子树中的函数f的最大值。这样,我们在计算f(i)时,只需用O(log n)时间找出不比d[i]大的最大数所对应的节点,并用O(1)的时间访问它的MAX域就可以得出f(i)的值。并且,插入操作和更新MAX域的操作也都只用O(log n)的时间(我们不需要删除操作),故总时间复杂度为O(n log n)。实际运行时这样的程序也是十分快的,n=10000时用不到1秒就可以得出结果,而原来的程序需要30秒。
从以上的讨论可以看出,再从程序设计上对问题优化时,要尽量减少问题的约束,尽可能的化为情况1。若不可以变为情况1,那么就要仔细考虑数据上的联系,设计好的数据结构来解决问题。
- 方程上的优化:
对于方程上的优化,其主要的方法就是通过某些数学结论对方程进行优化,避免不必要的运算。对于某一些特殊的问题,我们可以使用数学分析的方法对写出的方程求最值,这样甚至不用状态之间的递推计算就可以解决问题。不过用该方法解决的问题数量是在有限,并且这个方法也十分复杂。不过,却的确有相当数量的比较一般的问题,在应用某些数学结论后,可以提高程序的效率。
一个比较典型的例子是最优排序二叉树问题(CTSC96)。它的规划方程如下:
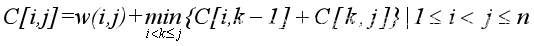
在递推时,阶段之间时没有优化的余地的,故优化的重点就在于这个方程的优化上。我们用B[i, j]表示D[i]+w(i, j),而原算法就是求出B并对每一列求最小值。
事实上,这一题的w有其特殊的性质:
对于a£ b£ c£ d,我们有w(a, c)+ w(b, d)£ w(a, d)+ w(b, c)。
这一性质对解题是应该有所帮助的。仿照上例,在两侧加上D[a]+ D[b],可得B[a, c]+ B[b, d]£ B[a, d]+ B[b, c]。
也就是说,若B[a, c]³ B[b, c],则有B[a, d]³ B[b, d]。于是我们在确定了B[a, c]与B[b, c]的大小关系之后,就可以决定是不是需要比较B[a, d]与B[b, d]的大小。
更进一步的,我们只要找出满足B[a, h]³ B[b, h]的最小的h,就可以免去h之后对第a列的计算。而这样的h,我们可以用二分查找法在O(log n)时间内找到(若w更特殊一些,例如说是确定的函数,我们甚至可以在O(1)的时间找到)。并且对于每一行来说,都只需要执行一次二分查找。在求出所有的h之后,只需用O(n)的时间对每列的第h行求值就可以了。这样得出的总时间为O(n)+O(n log n)= O(n log n)。至于程序设计上的问题,虽然并不复杂,但不是15分钟所可以解决的,也不是重点,略过不谈。[2]不过由于该题目可以用滚动数组的技巧解决空间的问题,故在大数据量时该算法有优异的表现。
从上面的叙述可以看出,对于方程的优化主要取决于权函数w的性质。其中应用最多的就是w(a, c)+ w(b, d)£ w(a, d)+ w(b, c)这个不等式。实际上,这个式子被称作函数的凸性判定不等式。在实际问题中,权函数通常都会满足这个不等式或这是它的逆不等式。故这样的优化应用是比较广泛的。还有许多特殊的不等式,若可以在程序中应用,都可以提高程序的效率。
- 从低维向高维的转化:
在问题扩大规模时,有一种方式就是扩大问题的维数。这时,规划时决策变量的维数也要增加。这样,存储的空间也要随着成指数级增加,导致无法存储下所有的状态,这就是动态规划的维数灾难问题。如果我们还要在这种情况下使用动态规划,那么就要使用极其复杂的数学分析方法。对于我们来说,使用这种方法显然是不现实的。这时,我们就需要改造动态规划的模型。通常我们都可以把这时的动态规划模型变为网络流模型。
对于模型的转化方法,我们有一些一般的规律。若状态转移方程只与另一个状态有关,我们可以肯定得到一个最小费用最大流的模型[3]。这个模型必然有其规律的地方,甚至用对偶算法在对网络流的求解时也还要用到动态规划的方法。不过这不是重点,我们关心的只是动态规划问题如何转化。例如说IOI’97《火星探测器》一题。这一题的一维模型是可以用动态规划来解决的(这里的维数概念是指探测器的数目)。在维数增加时,我们就可以用该方法来用网络流的方法解决问题。
除此之外,还有许多问题可以用该方法解决。例如最长区间覆盖问题,在维数增加时也同样可以用该方法解决。更进一步来说,甚至图论的最短路问题也可以做同样的转化来求出特殊的最短路。不过一般来说转化后流量最大为1,有许多特殊的性质也没有得到应用,并且些复杂的动态规划问题还无法转化为网络流问题(例如说最优二叉树问题),故标准的网络流算法显然有些浪费,它的解决还需要进一步的研究。
参考文献:
[EGG88] David Eppstein, Zvi Galil and Raffaele Giancarlo, Speeding up Dynamic Programming
[GP90] Zvi Galil and Kunsoo Park, Dynamic Programming with Convexity, Concavity, and Sparsity
[附录]
我们设k=Kb,c,则有C[a, c]+ C[b, d]£ C[a, k-1]+ C[k, c]+ C[b, k-1]+ C[k, d]+ w(a, c)+ w(b, d)= C[a, k-1]+ C[k, d]+ w(a, d)+ C[b, k-1]+ C[k, c]+ w(b, c)= C[a, d]+ C[b, c]。得证。
begin
E[1]ßD[1];
Queue.Add(K:1, H:n);
for jß2 to n do
begin
if B(j-1, j)£ B(Queue.K[head], j) then
begin
E[j]ßB(j-1, j);
Queue.Empty;
Queue.Add(K:j-1, H:n+1);
end else
begin
E[j]ßB(Queue.K[head], j);
while B(j-1, Queue.H[tail-1])£ B(Queue.K[tail], Queue.H[tail-1]) do Queue.Delete(tail);
Queue.H[tail]ßh(Queue.K[tail], j-1);
if h_OK then Queue.Add(K:j-1, H:n+1);
end;
if Queue.H[head]=j+1 then Queue.SkipHead;
end;
end;
其中的队列Queue可以称作备选队列,其中的队列头为第j行的最小值,并假设Queue.H[0]=j。其中的h(a, b)函数是用二分查找法查找B(a, h)³ B(b, h)的最小的h值,h_OK为查找成功与否的标志。在备选队列Queue中的数据(K:ir, H:hr)的意义是:当行数在区间[hr-1, hr-1]的范围内时,第ir列为最小值。我们知道,动态规划实际是求无向图的最短路的一种方法,故我们可以把动态规划中的每一个状态看成一个点,并将状态的转移过程变为一个图。在转化为最小费用最大流时,我们把这一个点拆成两个点,一个出点和一个入点,所有指向原来这个点的边都与入点相连,且所有由原来这个点发出的边现都以出点为起点。原来的边的容量设为正无穷,边权值一般不变。新增的入点与出点之间连一条边,它的权值为点权值,容量为每一点可以经过的次数(一般为一)。并且建立一个超级源和一个超级汇,并与可能的入点和出点连边。若有必要,超级源(或汇)也要拆成两个点,并且两个点之间的边的容量为最大的可能容量,边权值为0。这样,用最小费用流的方法得出的解就是该问题多维情况下的接。