一、什么是跳表

二、跳表的效率验证

三、跳表的实现

1、search

2、add

3、erase

四、跳表与其它搜索结构对比

总结

一、什么是跳表

跳表是一个随机化的数据结构，可以被看做二叉树的一个变种，它在性能上和红黑树，AVL树不相上下，但是跳表的原理非常简单，目前在Redis和LeveIDB中都有用到。

它采用随机技术决定链表中哪些节点应增加向前指针以及在该节点中应增加多少个指针。跳表结构的头节点需有足够的指针域，以满足可能构造最大级数的需要，而尾节点不需要指针域。

采用这种随机技术，跳表中的搜索、插入、删除操作的时间均为O(logn)，然而，最坏情况下时间复杂性却变成O(n)。相比之下，在一个有序数组或链表中进行插入/删除操作的时间为O(n)，最坏情况下为O(n)。

跳表是由skiplist是由William Pugh发明的，最早出现于他在1990年发表的论文《Skip Lists: A

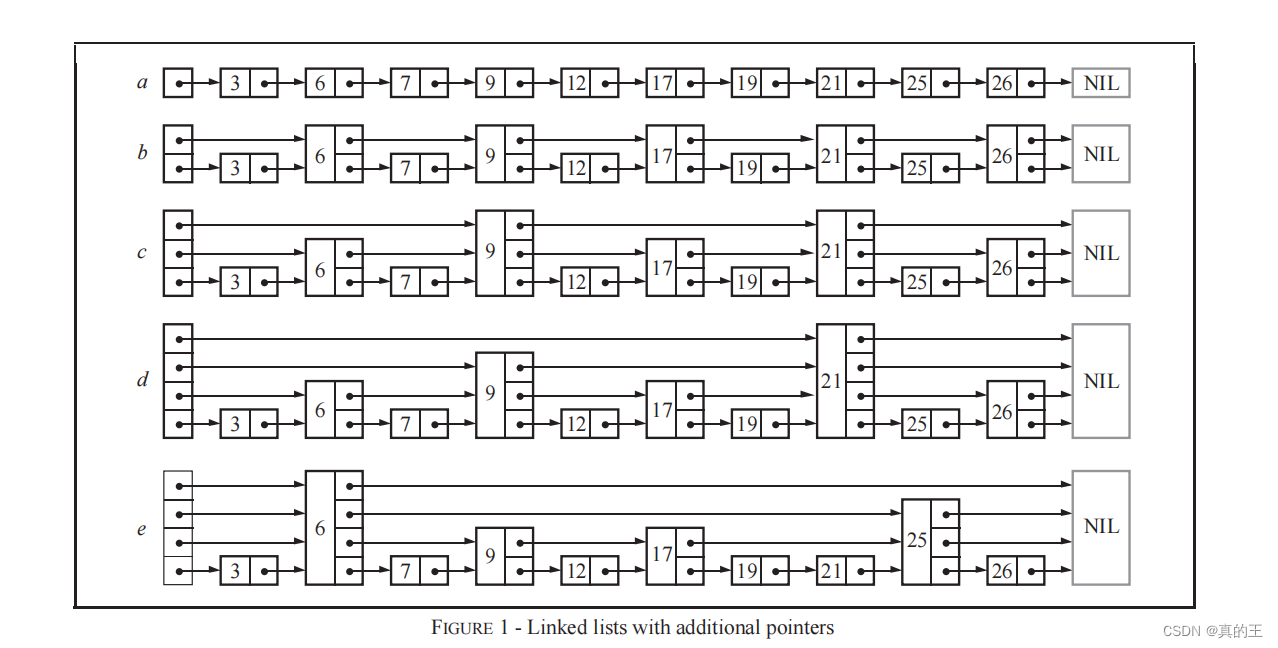
Probabilistic Alternative to Balanced Trees 》 skiplists (cmu.edu)

跳表的本质还是一个链表，它在一定程度上改善了链表的查询效率，相邻结点的高度可能是不相同的，上图是一种比较理想的情况，它的每个节点高度都是不相同且呈现一定的规律

不过这种情况太过理想，实际上，按照上面生成链表的方式，上面每一层链表的节点个数，是下面一层的节点个数的一半，这样查找过程就非常类似二分查找，使得查找的时间复杂度可以降低到O(log n)。但是这个结构在插入删除数据的时候有很大的问题，插入或者删除一个节点之后，就会打乱上下相邻两层链表上节点个数严格的2:1的对应关系。如果要维持这种对应关系，就必须把新插入的节点后面的所有节点（也包括新插入的节点）重新进行调整，这会让时间复杂度重新蜕化成O(n)。

skiplist的设计为了避免这种问题，做了一个大胆的处理，不再严格要求对应比例关系，而是插入一个节点的时候随机出一个层数。这样每次插入和删除都不需要考虑其他节点的层数，这样就好处理多了。这样就相当于将每个节点独立出来，只需要考虑当前节点的层数

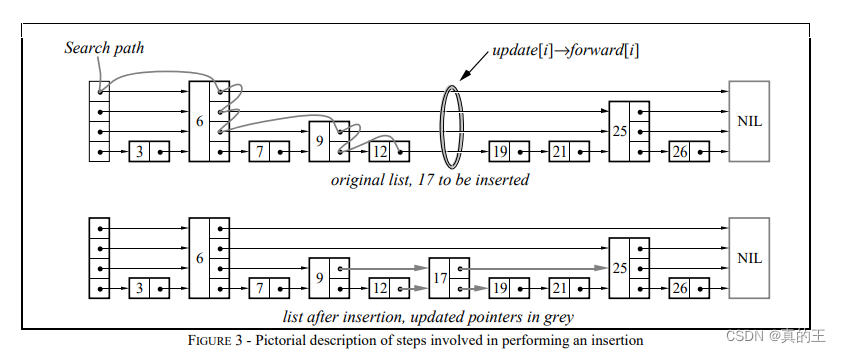
我们以跳表c来举例，在c中查询17这个节点

它的具体过程是：

首先有一个cur指针指向头节点的最高层，从头节点的最高层开始，如果同层的下一个节点的值比它小，就向右走：9比17小，cur指向9

如果同层的下一个节点的值比它大，就向下走：21比17大，cur走到9的第二层

同层的下一个节点的值与它相等，就找到了

如果走到了尾(nullptr)或者走到了-1层，那么就没有找到

二、跳表的效率验证

根据上面查询的过程我们可以大概估计它的时间复杂度是O(logN)

同时William Pugh给出了节点高度随机值的范围，如果没有限定范围随机出了10W，难道要建立10W层吗？

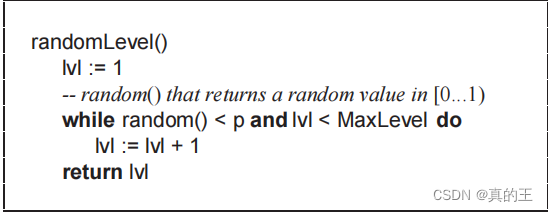
P：增加一层节点的概率

MaxLevel：节点层数的最大值

一般而言：P定为0.25，MaxLevel定为32层

我们可以使用加权平均值计算出跳表的平均高度

第一层的概率 1 - P

第二层的概率(1 - P) * P

第三层的概率(1 - P) * P * P

第n层的概率 (1 - P) * P ^(n - 1)

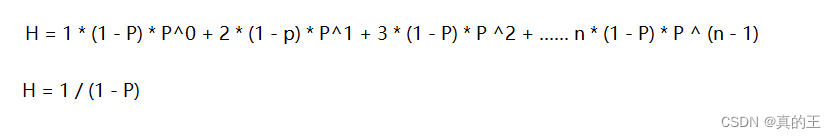
当P = 0.5时 H = 2

P = 0.25时 H = 1.3333

也就是说跳表节点高度不会太高

三、跳表的实现

1206. 设计跳表 - 力扣（LeetCode）

我们以这道题举例并且验证跳表的正确性

首先是跳表的节点

struct SkiplistNode
{
    int _val;
    std::vector<SkiplistNode*> _nextV;

    SkiplistNode(int val, int level)
        :_val(val)
        ,_nextV(level, nullptr)
    {}

};

跳表实际上是多维链表，节点的高度用一个vector来表示

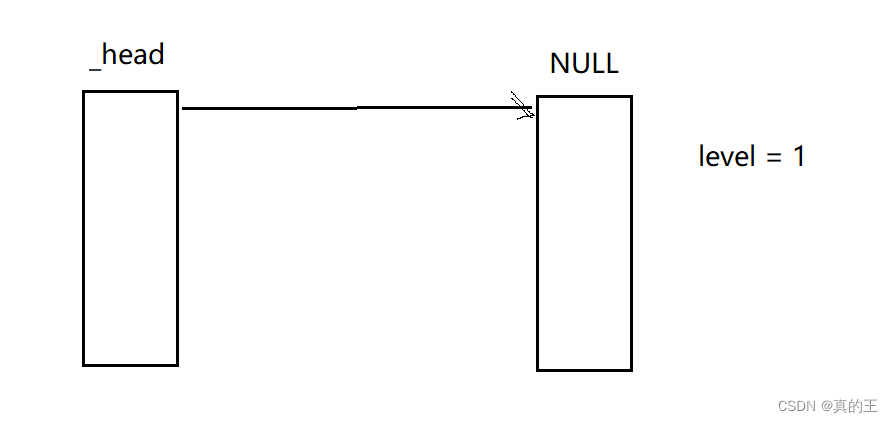
跳表的基本框架

class Skiplist {
    typedef SkiplistNode Node;
public:
    Skiplist() {
        _head = new Node(-1, 1);//创建一个头节点
    }
    

private:
    Node* _head;
    size_t _maxLevel = 32;
    double _p = 0.25;
};

1、search

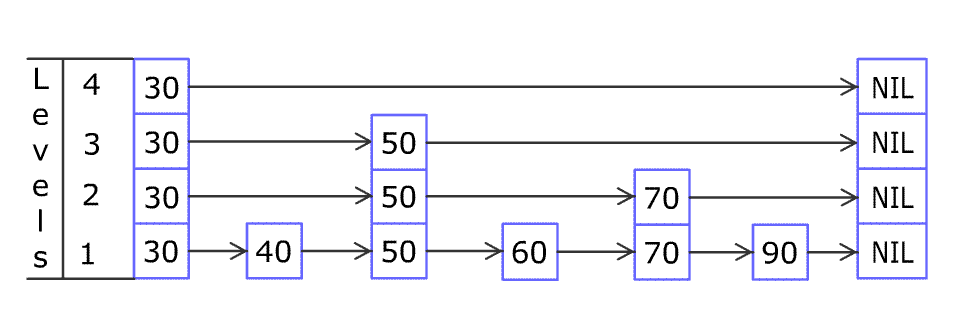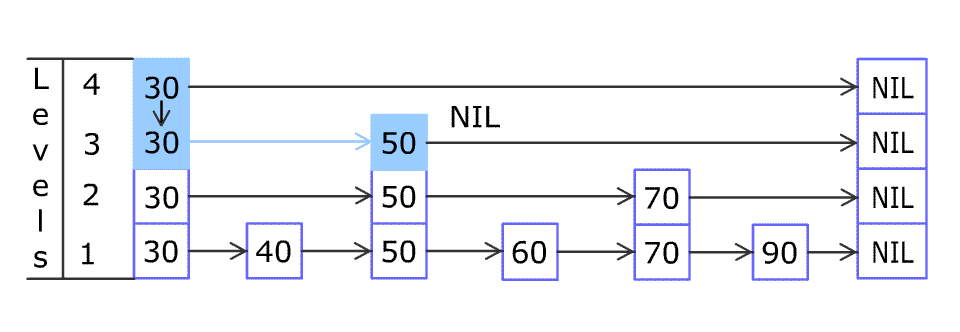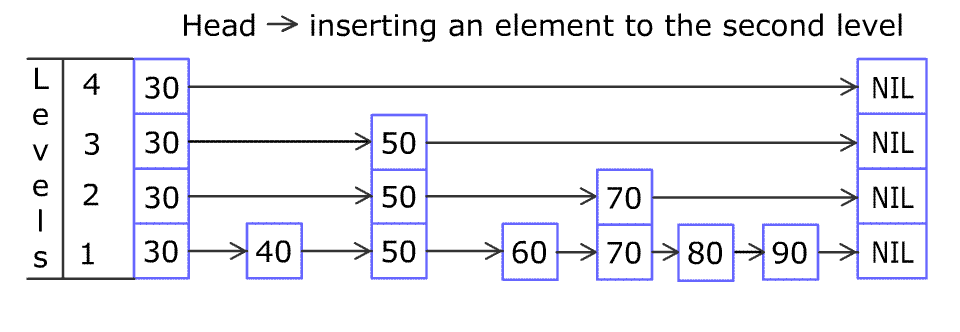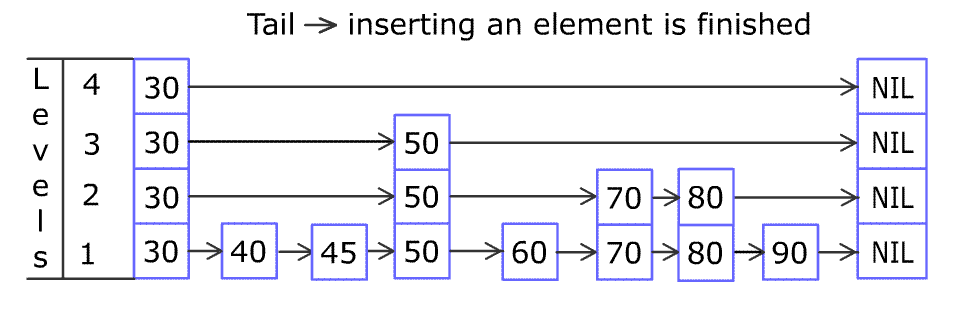
首先search 19这个能够找到的节点

cur首先走到6，6的下一个是空，cur走到6的下一层，6的下一个是25，25大于19，cur再向下走一层，cur的下一个是9，19大于9，cur走到9，9的下一个是25，25大于19，cur走到9的下一层，

9的下一个是12，12小于19，cur走到12，12的下一个是19，找到了

然后是找17这个节点

前面走到12的过程完全一样，现在走到12，12的下一个是19，比17大，cur走到12的下一层，12已经走到了最后一层，它的下一层是-1，结束，没有找到

还有一种情况是找28，走到26，26的下一个是空，结束，没有找到

    bool search(int target) {
        Node* cur = _head;
        int level = _head->_nextV.size() - 1;
        while(level >= 0)
        {
            if(cur->_nextV[level] && cur->_nextV[level]->_val < target)
            {
                cur = cur->_nextV[level];
            }
            else if(cur->_nextV[level] == nullptr || cur->_nextV[level]->_val > target)
            {
                level--;
            }
            else
            {
                return true;
            }
        }
        return false;
    }

2、add

add与链表类似，首先是找到要插入节点位置的前一个节点

找到插入节点的前一个节点的过程与search类似

使用一个vector来存储search过程中的prev节点

注意：这里只记录当向下移动时的节点，因为我们所谓的前一个节点指的是寻找一组target节点之前的每一层的前一个节点，只有在向下移动时才找到了当前层的target之前的节点

    std::vector<Node*> FindPrevNode(int num)
    {
        Node* cur = _head;
        int level = _head->_nextV.size() - 1;
        std::vector<Node*> prevV(_maxLevel, _head);

        while(level >= 0)
        {
            if(cur->_nextV[level] && cur->_nextV[level]->_val < num)
            {
                cur = cur->_nextV[level];
            }
            else
            {
                prevV[level] = cur;
                level--;
            }
        }

        return prevV;
    }

我们接收返回值，获取插入节点之前的每一层的prev节点

然后对于插入节点确定高度

这里使用C语言风格的随机值

    size_t RandomLevel()
    {
        size_t level = 1;
        while(rand() <= RAND_MAX * _p && level < _maxLevel)
        {
            level++;
        }

        return level;
    }

之后就是普通的链表插入节点的过程

    void add(int num) {
        std::vector<Node*> prevV = FindPrevNode(num);

        int n = RandomLevel();
        Node* newNode = new Node(num, n);
        if(n > _head->_nextV.size())
        {
            _head->_nextV.resize(n, nullptr);
        }

        for(size_t i = 0; i < n; i++)
        {
            newNode->_nextV[i] = prevV[i]->_nextV[i];
            prevV[i]->_nextV[i] = newNode;
        }
    }

3、erase

erase之前也需要我们获取它的前一个节点，我们还是查找它的前一个节点，然后手动判断一下，它的下一个节点的值是否是我们想要删除的节点的值，如果不是则证明该节点不存在

反之存在，就删除它，删除的过程也就不必多说

    bool erase(int num) {
        std::vector<Node*> prevV = FindPrevNode(num);

        if(prevV[0]->_nextV[0] == nullptr || prevV[0]->_nextV[0]->_val != num)
        {
            return false;
        }

        Node* del = prevV[0]->_nextV[0];
        
        for(size_t i = 0; i < del->_nextV.size(); i++)
        {
            prevV[i]->_nextV[i] = del->_nextV[i];
        }
        delete del;

        return true;
    }

同时这里还有一个优化的空间，如果删除的节点是跳表的最高节点，那么可以考虑降低头节点的高度

       //压缩高度
        int hight = _head->_nextV.size() - 1;
        while(hight >= 0)
        {
            if(_head->_nextV[hight] == nullptr)
            {
                hight--;
            }
            else
            {
                break;
            }
        }

        _head->_nextV.resize(hight + 1);

erase完整代码

    bool erase(int num) {
        std::vector<Node*> prevV = FindPrevNode(num);

        if(prevV[0]->_nextV[0] == nullptr || prevV[0]->_nextV[0]->_val != num)
        {
            return false;
        }

        Node* del = prevV[0]->_nextV[0];
        
        for(size_t i = 0; i < del->_nextV.size(); i++)
        {
            prevV[i]->_nextV[i] = del->_nextV[i];
        }
        delete del;

        //压缩高度
        int hight = _head->_nextV.size() - 1;
        while(hight >= 0)
        {
            if(_head->_nextV[hight] == nullptr)
            {
                hight--;
            }
            else
            {
                break;
            }
        }

        _head->_nextV.resize(hight + 1);

        return true;
    }

完整代码

struct SkiplistNode
{
    int _val;
    std::vector<SkiplistNode*> _nextV;

    SkiplistNode(int val, int level)
        :_val(val)
        ,_nextV(level, nullptr)
    {}

};

class Skiplist {
    typedef SkiplistNode Node;
public:
    Skiplist() {
        srand(time(0));
        _head = new Node(-1, 1);
    }
    
    bool search(int target) {
        Node* cur = _head;
        int level = _head->_nextV.size() - 1;
        while(level >= 0)
        {
            if(cur->_nextV[level] && cur->_nextV[level]->_val < target)
            {
                cur = cur->_nextV[level];
            }
            else if(cur->_nextV[level] == nullptr || cur->_nextV[level]->_val > target)
            {
                level--;
            }
            else
            {
                return true;
            }
        }
        return false;
    }

    size_t RandomLevel()
    {
        size_t level = 1;
        while(rand() <= RAND_MAX * _p && level < _maxLevel)
        {
            level++;
        }

        return level;
    }

    std::vector<Node*> FindPrevNode(int num)
    {
        Node* cur = _head;
        int level = _head->_nextV.size() - 1;
        std::vector<Node*> prevV(_maxLevel, _head);

        while(level >= 0)
        {
            if(cur->_nextV[level] && cur->_nextV[level]->_val < num)
            {
                cur = cur->_nextV[level];
            }
            else
            {
                prevV[level] = cur;
                level--;
            }
        }

        return prevV;
    }
    
    void add(int num) {
        std::vector<Node*> prevV = FindPrevNode(num);

        int n = RandomLevel();
        Node* newNode = new Node(num, n);
        if(n > _head->_nextV.size())
        {
            _head->_nextV.resize(n, nullptr);
        }

        for(size_t i = 0; i < n; i++)
        {
            newNode->_nextV[i] = prevV[i]->_nextV[i];
            prevV[i]->_nextV[i] = newNode;
        }
    }
    
    bool erase(int num) {
        std::vector<Node*> prevV = FindPrevNode(num);

        if(prevV[0]->_nextV[0] == nullptr || prevV[0]->_nextV[0]->_val != num)
        {
            return false;
        }

        Node* del = prevV[0]->_nextV[0];
        
        for(size_t i = 0; i < del->_nextV.size(); i++)
        {
            prevV[i]->_nextV[i] = del->_nextV[i];
        }
        delete del;

        //压缩高度
        int hight = _head->_nextV.size() - 1;
        while(hight >= 0)
        {
            if(_head->_nextV[hight] == nullptr)
            {
                hight--;
            }
            else
            {
                break;
            }
        }

        _head->_nextV.resize(hight + 1);

        return true;
    }
private:
    Node* _head;
    size_t _maxLevel = 32;
    double _p = 0.25;
};

四、跳表与其它搜索结构对比

1. skiplist 相比平衡搜索树 (AVL 树和红黑树 ) 对比，都可以做到遍历数据有序，时间复杂度也差不多。skiplist 的优势是： a 、 skiplist 实现简单，容易控制。平衡树增删查改遍历都更复杂。b、skiplist 的额外空间消耗更低。平衡树节点存储每个值有三叉链，平衡因子 / 颜色等消耗。skiplist中 p=1/2 时，每个节点所包含的平均指针数目为 2 ； skiplist 中 p=1/4 时，每个节点所包

含的平均指针数目为 1.33 ；

2. skiplist 相比哈希表而言，就没有那么大的优势了。相比而言 a 、哈希表平均时间复杂度是O(1)，比 skiplist 快。 b 、哈希表空间消耗略多一点。 skiplist 优势如下： a 、遍历数据有序b、 skiplist 空间消耗略小一点，哈希表存在链接指针和表空间消耗。 c 、哈希表扩容有性能损耗。d 、哈希表再极端场景下哈希冲突高，效率下降厉害，需要红黑树补足接力。