【LetMeFly】1572.矩阵对角线元素的和

力扣题目链接：https://leetcode.cn/problems/matrix-diagonal-sum/

给你一个正方形矩阵 mat，请你返回矩阵对角线元素的和。

请你返回在矩阵主对角线上的元素和副对角线上且不在主对角线上元素的和。

 

示例  1：

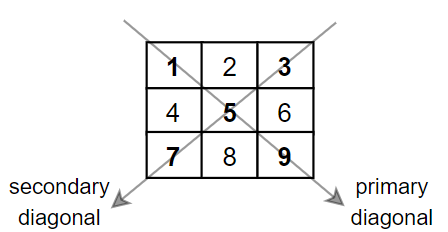
输入：mat = [[1,2,3],
            [4,5,6],
            [7,8,9]]
输出：25
解释：对角线的和为：1 + 5 + 9 + 3 + 7 = 25
请注意，元素 mat[1][1] = 5 只会被计算一次。

示例  2：

输入：mat = [[1,1,1,1],
            [1,1,1,1],
            [1,1,1,1],
            [1,1,1,1]]
输出：8

示例 3：

输入：mat = [[5]]
输出：5

 

提示：

• n == mat.length == mat[i].length
• 1 <= n <= 100
• 1 <= mat[i][j] <= 100

方法一：模拟

假设$mat$的大小是$n\times n$，则可以：

用$i$从$0$到$n-1$遍历$mat$的每一行，$ans$加上这一行的$i$和$n-i-1$。

最后，如果$n$是奇数，则还需要减去对主副对角线重叠的元素$mat[\lfloor \frac{n}{2}\rfloor ][\lfloor \frac{n}{2}\rfloor ]$

• 时间复杂度$O(n)$，其中$size(mat)=n\times n$
• 空间复杂度$O(1)$

AC代码

C++

class Solution {
public:
    int diagonalSum(vector<vector<int>>& mat) {
        int n = mat.size();
        int ans = 0;
        for (int i = 0; i < n; i++) {
            ans += mat[i][i] + mat[i][n - i - 1];
        }
        if (n % 2) {
            ans -= mat[n / 2][n / 2];
        }
        return ans;
    }
};

Python

# from typing import List

class Solution:
    def diagonalSum(self, mat: List[List[int]]) -> int:
        n = len(mat)
        ans = 0
        for i in range(n):
            ans += mat[i][i] + mat[i][n - i - 1]
        if n % 2:
            ans -= mat[n // 2][n // 2]
        return ans

同步发文于CSDN，原创不易，转载请附上原文链接哦~
Tisfy：https://letmefly.blog.csdn.net/article/details/132223172