stack 基本概念

定义

在C++中，栈（stack）是一种常见的数据结构，采用后进先出（Last-In-First-Out，LIFO）的原则。栈的特点是它只有一个出口，只允许在一端进行插入和删除操作，这一端被称为栈顶。在栈中，只有位于栈顶的元素可以被访问和操作，而其他元素则无法直接访问。栈中只有顶端的元素才可以被外界使用，因此栈不允许有遍历行为

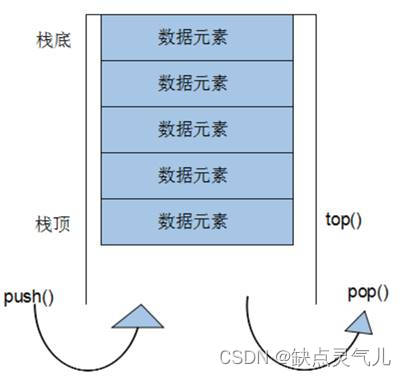
基本概念

栈顶（Top）——指向栈中最上面的元素的位置。

入栈（Push）——将元素添加到栈顶。

出栈（Pop）——从栈顶移除元素。

栈空（Empty）——当栈中没有任何元素时，称为栈空。

栈大小（Size）——表示栈中元素的数量。

stack 常用接口

构造函数

• stack<T> stk; stack采用模板类实现， stack对象的默认构造形式
• stack(const stack &stk); 拷贝构造函数

赋值操作

• stack& operator=(const stack &stk); 重载等号操作符

数据存取

• push(elem); 向栈顶添加元素
• pop(); 从栈顶移除第一个元素
• top(); 返回栈顶元素

大小操作

• empty(); 判断堆栈是否为空
• size(); 返回栈的大小

示例

代码

#include <iostream>
#include <stack>

int main() {
    std::stack<int> stk;

    // 判断栈是否为空
    if (stk.empty()) {
        std::cout << "栈为空" << std::endl;
    }

    // 向栈中添加元素
    stk.push(10);
    stk.push(20);
    stk.push(30);

    // 返回栈顶元素
    std::cout << "栈顶元素为：" << stk.top() << std::endl;

    // 移除栈顶元素
    stk.pop();

    // 再次返回栈顶元素
    std::cout << "栈顶元素为：" << stk.top() << std::endl;

    // 获取栈的大小
    std::cout << "栈的大小为：" << stk.size() << std::endl;

    return 0;
}

运行结果如下：

栈为空
栈顶元素为：30
栈顶元素为：20
栈的大小为：2

分析

这个例子创建了一个整型的栈对象std::stack stk
然后通过empty()方法判断栈是否为空
接着使用push(elem)方法向栈中依次添加元素10、20和30。 使用top()方法可以获取栈顶元素的值
然后使用pop()方法移除栈顶元素
最后使用size()方法返回栈的大小。

总结

• 入栈 — push
• 出栈 — pop
• 返回栈顶 — top
• 判断栈是否为空 — empty
• 返回栈大小 — size

常见的应用场景

函数调用和递归

在函数调用中，每当进入一个新的函数时，函数的调用信息（如返回地址、局部变量等）可以通过栈顶入栈，待函数执行完成后，这些信息会从栈顶依次出栈，实现了函数调用的递归和返回。

表达式求值

在一些需要解析表达式的场景中，可以使用栈来实现表达式的求值。例如，中缀表达式转换为后缀表达式，再利用栈对后缀表达式进行求值。

括号匹配

在处理括号匹配问题中，可以使用栈来验证括号是否配对。遇到左括号时，将其入栈；遇到右括号时，判断栈顶元素是否是对应的左括号，如果是，则将栈顶元素出栈，继续判断下一个字符；如果不是，说明括号不匹配。

浏览器的前进后退功能

在浏览器的前进后退功能中，可以使用两个栈来实现。一个栈用于存储用户访问的页面历史记录，另一个栈用于存储用户点击后退按钮时需要返回的页面历史记录。

撤销操作

在一些文本编辑器、绘图软件等应用中，可以使用栈来实现撤销操作。每当用户进行操作时，将操作的信息存储在栈中，在需要撤销操作时，从栈顶取出最近的操作信息进行回滚。

在深度优先搜索（DFS）算法中，可以使用栈来实现对图或树的遍历。

将起始节点入栈，然后循环执行以下步骤：从栈顶弹出一个节点，访问该节点，将其未访问过的邻居节点入栈。重复执行直到栈为空。

在迷宫求解问题中，可以使用栈来实现回溯算法。

将起始位置入栈，然后循环执行以下步骤：从栈顶弹出一个位置，尝试向上、下、左、右四个方向移动，如果可以移动则更新位置并入栈，直到找到目标位置或者栈为空。