【LetMeFly】1289.下降路径最小和 II：通俗易懂地讲解O(n^2) + O(1)的做法

力扣题目链接：https://leetcode.cn/problems/minimum-falling-path-sum-ii/

给你一个 n x n 整数矩阵 arr ，请你返回 非零偏移下降路径 数字和的最小值。

非零偏移下降路径 定义为：从 arr 数组中的每一行选择一个数字，且按顺序选出来的数字中，相邻数字不在原数组的同一列。

示例 1：

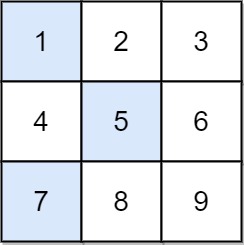
输入：arr = [[1,2,3],[4,5,6],[7,8,9]]
输出：13
解释：
所有非零偏移下降路径包括：
[1,5,9], [1,5,7], [1,6,7], [1,6,8],
[2,4,8], [2,4,9], [2,6,7], [2,6,8],
[3,4,8], [3,4,9], [3,5,7], [3,5,9]
下降路径中数字和最小的是 [1,5,7] ，所以答案是 13 。

示例 2：

输入：grid = [[7]]
输出：7

提示：

n == grid.length == grid[i].length
1 <= n <= 200
-99 <= grid[i][j] <= 99

方法一：动态规划

这道题其实思路很简单：

gird[i][j]来自gird[i - 1]的哪一个？当然是gird[i - 1]中最小的那一个。
如果grid[i - 1]中最小的那个元素恰好是j怎么办？那么gird[i][j]就来自gird[i - 1]中第二小的那一个。

不难发现，我们只关注上一行最小的两个元素（的位置）

具体实现

写一个函数findMin2(v)，用来寻找数组v中最小的两个元素的位置。

用 $i$ 从第2行开始遍历地图grid：

用 $j$ 遍历 $g i r d [i]$ ：
- 如果 $j$ 等于上一行最小元素的下标： $g r i d [i] [j] + = g r i d [i - 1] [第二小元素的下标]$
- 否则 $g r i d [i] [j] + = g r i d [i - 1] [最小元素的下标]$

最终返回最后一行的最小元素即可。

时间复杂度 $O(n^2)$ ，其中 $n\times n$
空间复杂度 $O (1)$

AC代码

C++

class Solution {
private:
    pair<int, int> findMin2(vector<int>& v) {  // 只接收长度大于等于2的v
        pair<int, int> ans;
        int m = v[0], loc = 0;
        for (int i = 0; i < v.size(); i++) {
            if (v[i] < m) {
                m = v[i], loc = i;
            }
        }
        ans.first = loc;
        loc = ans.first ? 0 : 1, m = v[loc];  // 如果第一个元素是最小的，那么找第二个最小元素的时候就从上一行的第二个元素开始
        for (int i = 0; i < v.size(); i++) {
            if (v[i] < m && i != ans.first) {
                m = v[i], loc = i;
            }
        }
        ans.second = loc;
        return ans;
    }
public:
    int minFallingPathSum(vector<vector<int>>& grid) {
        int n = grid.size();
        for (int i = 1; i < n; i++) {
            pair<int, int> last2min = findMin2(grid[i - 1]);  // i >= 1说明grid[i - 1].size() >= 2
            for (int j = 0; j < n; j++) {
                grid[i][j] += (j == last2min.first ? grid[i - 1][last2min.second] : grid[i - 1][last2min.first]);
            }
        }
        return *min_element(grid.back().begin(), grid.back().end());
    }
};

Python

# from typing import List

class Solution:
    def findMin2(self, v: List[int]) -> List[int]:
        ans = [0, 0]
        m, loc = v[0], 0
        for i in range(len(v)):
            if v[i] < m:
                m, loc = v[i], i
        ans[0] = loc
        loc = 0 if ans[0] else 1
        m = v[loc]
        for i in range(len(v)):
            if v[i] < m and i != ans[0]:
                m, loc = v[i], i
        ans[1] = loc
        return ans
    
    def minFallingPathSum(self, grid: List[List[int]]) -> int:
        n = len(grid)
        for i in range(1, n):
            last2min = self.findMin2(grid[i - 1])
            for j in range(n):
                grid[i][j] += grid[i - 1][last2min[0]] if j != last2min[0] else grid[i - 1][last2min[1]]
        return min(grid[-1])