这里给出一种简单高效的IMU姿态解算方法,本方法的特点就是思路非常的简单,并且效果也还可以,地面机器人这类运动想对不那么剧烈的应用应该是能应付的,但是震动较大的无人机、足式机器人等应用是否能应用还有待试验。
代码如下:
/**
* @brief 姿态估计
*
*/
void simpleAttitudeEstimation(const msa2d::sensor::ImuData& curr_data) {
// 第一个IMU数据不计算,只记录时间信息
if (last_attitude_predict_time_ == 0) {
last_attitude_predict_time_ = curr_data.time_stamp_;
last_attitude_update_time_ = last_attitude_predict_time_;
return;
}
const Eigen::Vector3d unbiased_gyro = curr_data.gyro_ - sensor_param_.imu_.gyro_bias_; // 去偏置
const Eigen::Vector3d angle_vec = unbiased_gyro * (curr_data.time_stamp_ - last_attitude_predict_time_);
const double angle = angle_vec.norm();
const Eigen::Vector3d axis = angle_vec / angle;
Eigen::Matrix3d delta_rot = Eigen::AngleAxisd(angle, axis).toRotationMatrix();
sensor_param_.imu_.G_R_I_ = sensor_param_.imu_.G_R_I_ * delta_rot; // 旋转矩阵姿态更新
last_attitude_predict_time_ = curr_data.time_stamp_;
/**
* @brief 在线标定陀螺仪bias
* 测试:使用在线标定,15min 角度最大漂移0.1rad
* 不使用在线标定,15min角度最大漂移 0.3rad
* @todo 为了节省计算量,采用了一种迭代的静止标定方法,局限是需要载体在静止时才会自动校准参数,
* 改进点是如何实现高效的动态标定
*/
imu_tool_.OnlineCalibGyroBias(unbiased_gyro, sensor_param_.imu_.gyro_bias_);
// 重力校正
float acc_v = curr_data.acc_.norm();
// 加速度不能和重力相差太大
if (std::fabs(acc_v - 9.8) < 0.3 * 9.8) {
double correct_delta_t = curr_data.time_stamp_ - last_attitude_update_time_;
// 至少间隔0.1s
if (correct_delta_t > 0.1) {
// 计算权重因子
float time_ratio = 1 - std::exp(-correct_delta_t / 0.5); // 距离上一次校正的时间间隔越大 越接近1
// 由重力观测出姿态角
float gravity_pitch = -std::asin(curr_data.acc_[0] / 9.81);
float gravity_roll = std::atan2(curr_data.acc_[1], curr_data.acc_[2]);
// 由陀螺仪观测出来的姿态角
float gyro_roll_ = atan2(sensor_param_.imu_.G_R_I_(2, 1), sensor_param_.imu_.G_R_I_(2, 2));
float gyro_pitch_ = asin(-sensor_param_.imu_.G_R_I_(2, 0));
// 重力解算出来的结果与陀螺仪解算出来的结果相差不能太大(5度)
// 否则由与短时间更加信任陀螺仪,所以认为重力观测不准
if (std::fabs(gyro_roll_ - gravity_roll) < 0.08 && std::fabs(gyro_pitch_ - gravity_pitch) < 0.08) {
// 加权融合
float correct_pitch = time_ratio * gravity_pitch + (1 - time_ratio) * gyro_pitch_;
float correct_roll = time_ratio * gravity_roll + (1 - time_ratio) * gyro_roll_;
// 重新更新旋转矩阵
sensor_param_.imu_.G_R_I_ = Eigen::AngleAxisd(0, Eigen::Vector3d::UnitZ())
* Eigen::AngleAxisd(correct_pitch, Eigen::Vector3d::UnitY())
* Eigen::AngleAxisd(correct_roll, Eigen::Vector3d::UnitX());
last_attitude_update_time_ = curr_data.time_stamp_;
}
}
}
}
解析:
简单来说也是和互补滤波、KF一样的加权融合,步骤如下:
1、陀螺仪角速度测量对旋转矩阵进行更新。
2、迭代静态在线校准陀螺仪bias。
3、将重力向量观测恢复成姿态角的观测,同时将陀螺仪更新的旋转矩阵也恢复成姿态角,对这两个姿态角进行加权融合。这一步对整个系统的效果影响最为关键的,可以尝试增加各种的trick去进行优化,这里采用了两个最基本的策略,(1)、加速度向量的模长不能比重力大太多,否则这个加速度观测大概率包含了机体自身的运动加速度,这个测量值是不可用的。(2)、陀螺仪短时间准确,而长时间有累计误差,加速度计短期噪声大,而长期比较准确,因此,将校正的时间间隔作为权重的考量因素,时间过的越久,就越不相信陀螺仪的结果,而更相信重力观测的结果。(3)、除了模长外,还要考虑由重力和陀螺仪单独恢复出来的姿态角之间的差异,校正只在两个姿态角接近的时候执行,因为,在重力观测可靠时,重力恢复的姿态角和陀螺仪恢复的姿态角之间的误差很小,而当这个误差很大时,大概率是由与剧烈运动所产生的加速度噪声引起的,因此过滤掉。
试验结果:
下面是姿态角pitch的角度图,蓝色是融合后的结果,红色是加速度单独计算的结果,黄色是角速度单独计算的结果。
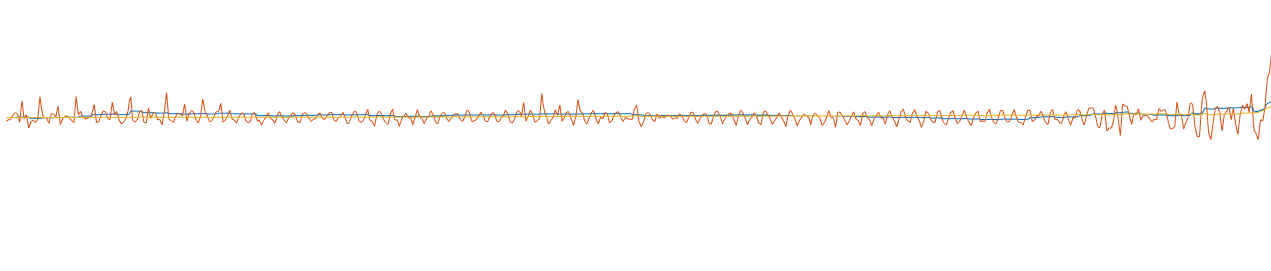 静止时,可以看到加速度解算的结果有很大的噪声。
静止时,可以看到加速度解算的结果有很大的噪声。
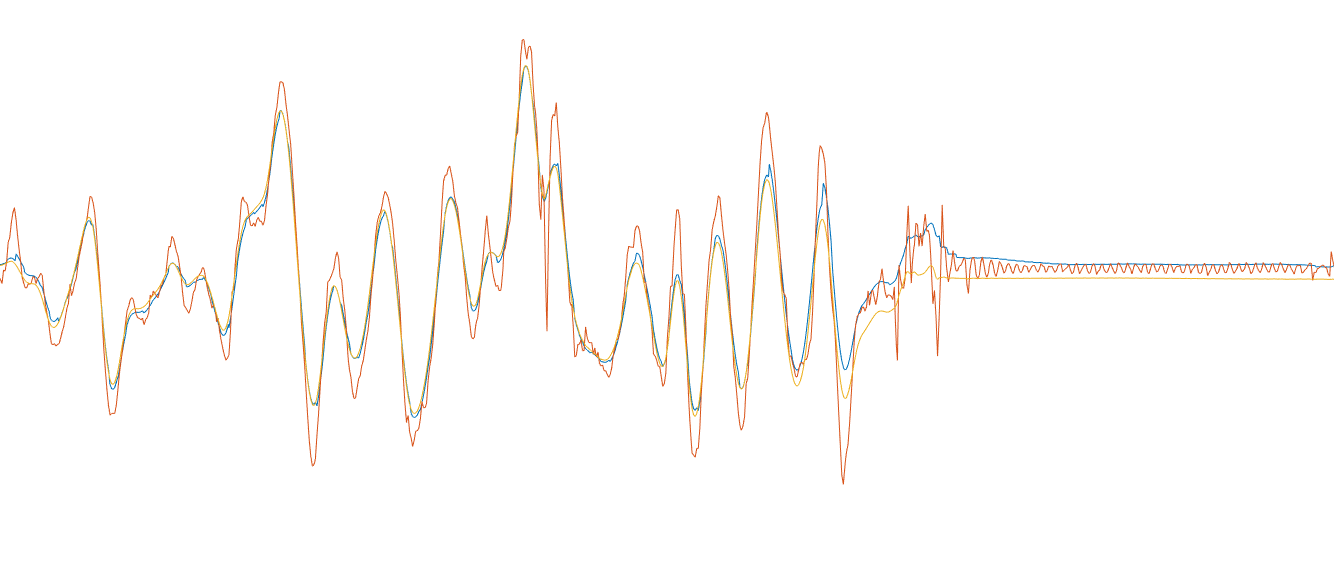 上图是缓慢旋转抖动产生的。
上图是缓慢旋转抖动产生的。
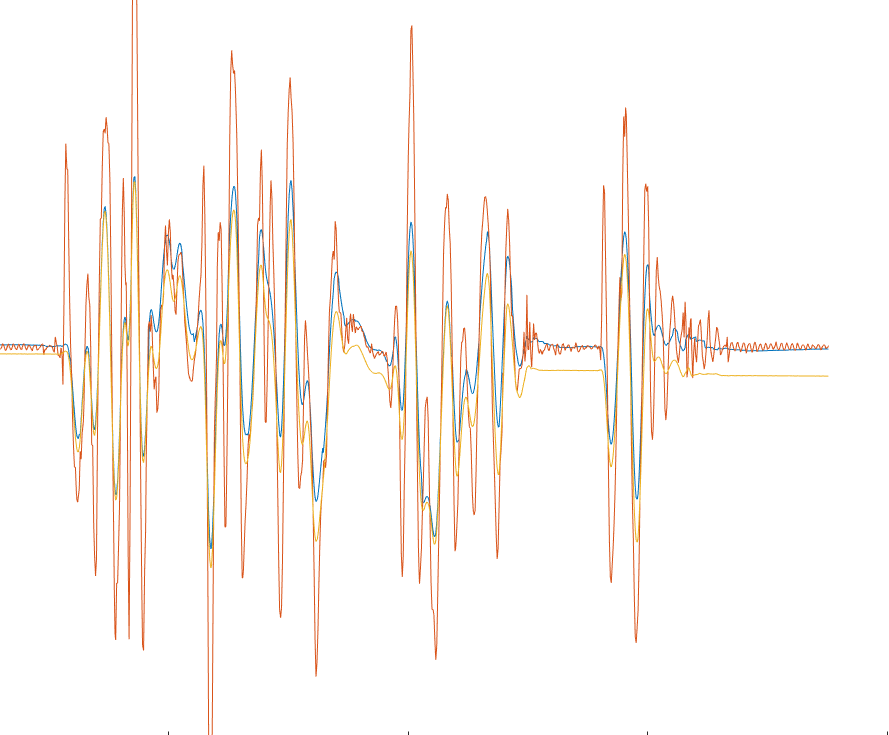 上图对应的是剧烈晃动,可以看到加速度计已经产生了巨大的噪声了,但融合后就将加速度计的噪声大部分过滤了,同时,最后静止时相比于陀螺仪的结果显著降低了稳态误差。
上图对应的是剧烈晃动,可以看到加速度计已经产生了巨大的噪声了,但融合后就将加速度计的噪声大部分过滤了,同时,最后静止时相比于陀螺仪的结果显著降低了稳态误差。
一些问题:
由与没有仔细调参,还是有不少问题的,如下图就没有很好的将加速度计的干扰给过滤掉。

剧烈运动时,给加速度的权重还是太大了,
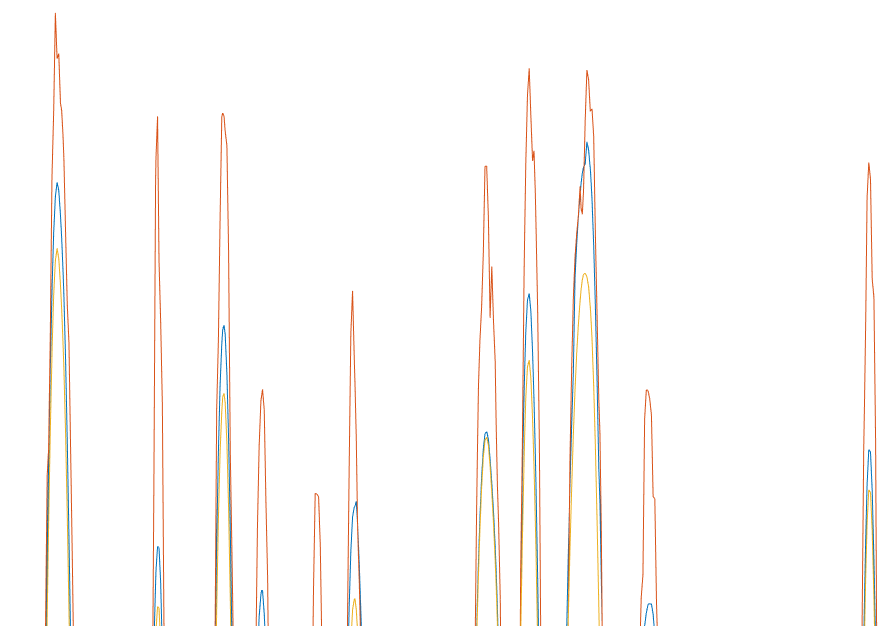
总之有空还得将参数再好好调一调,不过只要不是太剧烈的运动用起来还是可以的。