目录

题目：

示例：

分析：

代码：

---

题目：

示例：

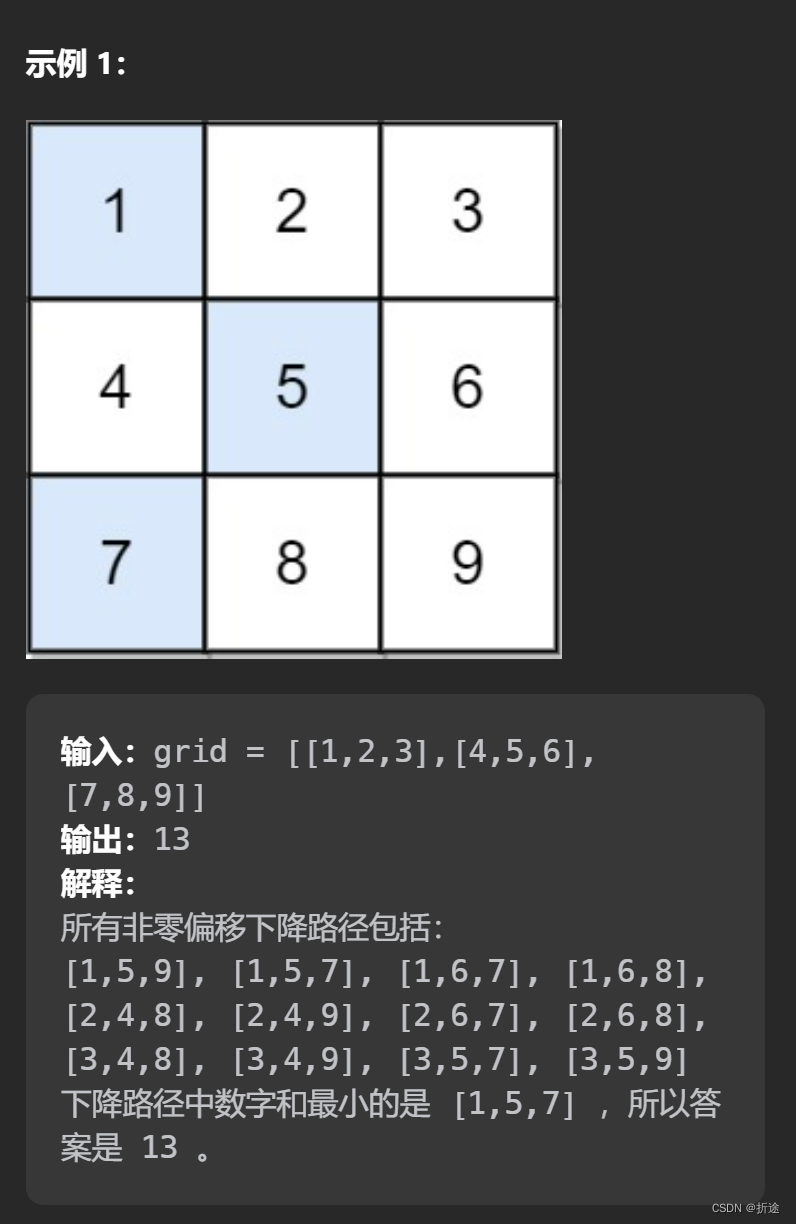
分析：

题目给我们一个数组，让我们模拟从上面第一层走到下面的最后一层，下降路径需要加上经过的格子的值，每层走的格子不能和相邻层走的格子在同一列，让我们返回下降路径的最小和。

那既然是要路径的总和最小，那么我每次都只选择最小的数不就好啦。

不过相邻行的最小元素所在的列可能是会一样的，这样我们就不能直接无脑选择最小了，我们每次选择本行经过哪一格的时候，需要做个判断，只要你这格子的列跟我上一行最小数的列不一样，那么我就在你这格子的值我再加上上一层的最小值，这样就可以表示我从上面的最小格走到你这边，这格的数就是我从上面走到这个格子的下降路径和，我们这样不断累加，直到最后统计最后一行的最小值，那就是总的下降路径最小和了。

不过还有一个问题，和上一行最小值的不同列的格子我们都更新数值了，那么同列的格子我们应该怎么更新呢？我们可以记录下第二小的数，如果一个格子和上一列的最小数同列，那么它就不会和第二小的数同列，既然无法加最小的数，那么退而求其次，我加上第二小的数也凑合。

所以我们需要维护两个变量，分别来存储上一层第一小的元素和列下标以及上一层第二小的元素和列下标。

我们还需要在遍历每层的时候就更新这两个变量，作为下一层的上一层最小元素，但是这样会造成数据污染，如果我还没遍历完整层元素就把这两个变量给更新了，那么本层中后面的格子可能用的就不是上一层的最小数而是本层的最小数了。

所以我们其实一共需要四个变量，两个变量一样是存储上一层的第一小和第二小的元素和列下标。另外两个变量就用来存储本层的第一小和第二小元素和列下标。在遍历完整层之后，再将上一层的两个变量更新为本层的两个变量。

最后我们返回最后一层的最小值，那就是我们要返回的下降路径最小和了。

代码：

class Solution {
public:
    int minFallingPathSum(vector<vector<int>>& grid) {
        int n=grid.size();
        if(n==1) return grid[0][0];
        pair<int,int>min1{-1,0},min2{-1,0}; //初始化成最小次小都为0,这样在第一层操作的时候就不会有影响

        for(int i=0;i<n;i++){
            pair<int,int>min11{0,INT_MAX},min22{0,INT_MAX}; //记录本层的最小和次小,用于更新
            for(int j=0;j<n;j++){
                if(j!=min1.first) grid[i][j]+=min1.second;  //如果不是和上层最小的列一样就添加最小.
                else grid[i][j]+=min2.second;   //反之添加次小.

                if(grid[i][j]<min11.second){    //更新本层的最小
                    min22=min11;    //最小更新以后,之前的最小就是现在的次小
                    min11.first=j;
                    min11.second=grid[i][j];
                }else if(grid[i][j]<min22.second){  //更新本层的次小
                    min22.first=j;
                    min22.second=grid[i][j];
                }
            }
            min1=min11;min2=min22;  //更新
        }
        return min1.second;
    }
};