剑指 Offer 56 - II. 数组中数字出现的次数 II
在一个数组 nums 中除一个数字只出现一次之外，其他数字都出现了三次。请找出那个只出现一次的数字。

 

示例 1：

输入：nums = [3,4,3,3]
输出：4
示例 2：

输入：nums = [9,1,7,9,7,9,7]
输出：1

通用版：
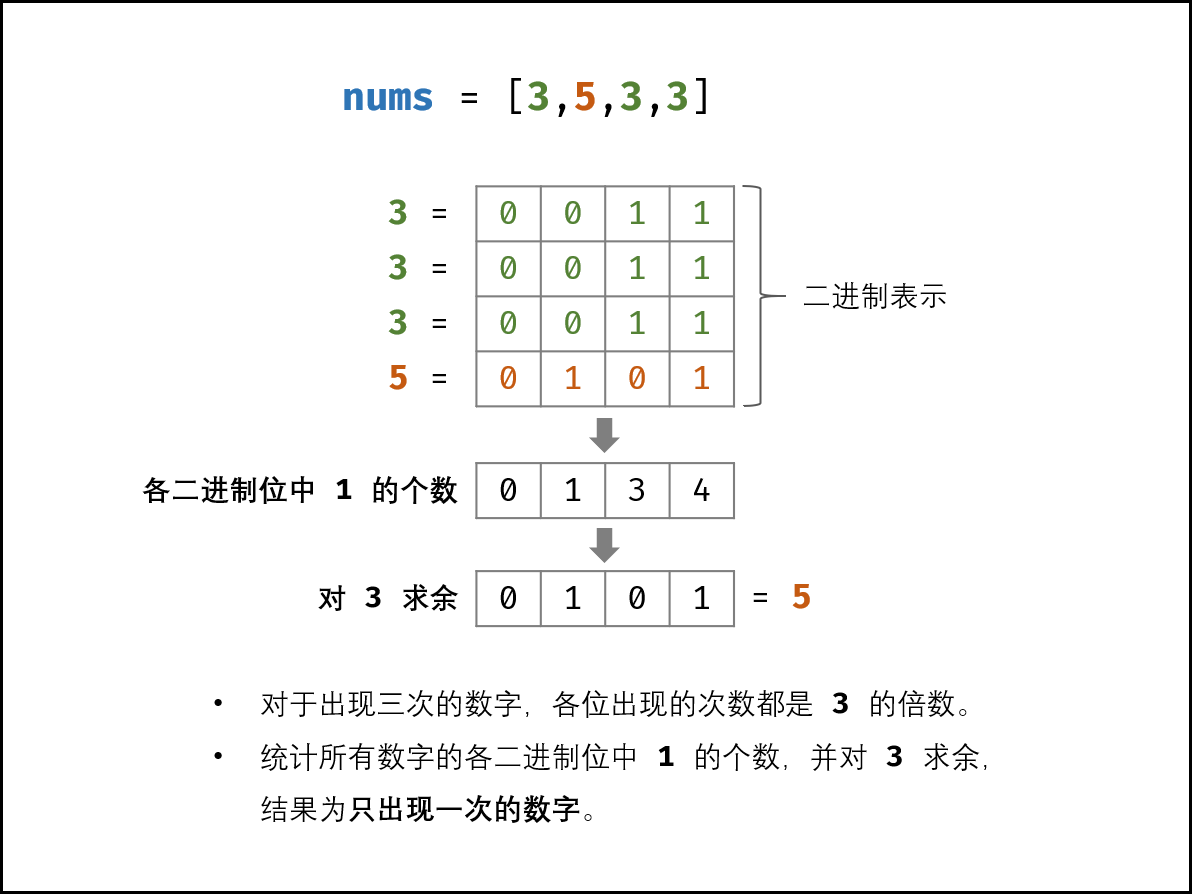
假设数组中，只有一个数出现1次，其余数都出现k次。问：这个“出现一次”的数是谁？

思路：
首先，将数组中每一位数转成二进制，
然后，对每一个二进制位做加法，第i位二进制记录到counts[i]中；
接着，counts[i]对k取余数，即counts[i]%k，（思考一下，此时那些出现k次的数的二进制表示的第i位，加和到counts[i]中，经过这次%k,他们的痕迹必然消失，所以此后count[i]就是那个“只出现一次”的数的二进制表示的第i位）；
最后，将counts这个二进制数组 转换成对应十进制数即可。

下面是我参考了力扣K神之后自己写的代码，还有K神的代码：
区别在于：counts[i]的定义不同。

class Solution {
// 我自己写的，count[0]表示高位，count[31]表示低位
    public int singleNumber1(int[] nums) {
        int[] count = new int[32];
        for(int num:nums){
            for(int j=31;j>=0;j--){
                count[j] += (num&1);
                num>>>=1;
            }
        }
        
        int res=0;
        for(int j=0;j<32;j++){
            res=2*res+(count[j]%3); //注意这里是二进制转十进制
        }
        return res;
    }



     public int singleNumber(int[] nums) {
     // 大佬写的，count[31]表示高位，count[0]表示低位
         int[] counts = new int[32];
         for(int num:nums){
             for(int j=0;j<32;j++){
                 counts[j] += (num&1);
                 num>>>=1;
             }
         }
         int res=0;
         for(int i=0;i<32;i++){   
         // 注意这两句话不要写反了，可以想想：i=31时，res应该记录最低位；而如果写反了，res记录完counts[0]，还会左移一位，此时最低位是0，这显然不对。          
             res<<=1;
             res|=(counts[31-i]%3);
             
         }
         return res;
     }
}

下面是《程序员代码面试指南》中解法
思路和上面相差不大，这里是把数组中每一个数转成k进制，每一位加和得到eo，
然后，对k取余数（注意考虑到“先求和再取余，等于，先取余再求和”，代码中这部分是一边求和一边取余），这一步之后那些“出现k次”的数在eo中必然没有留下痕迹，也就是说eo是我们要找那个“只出现一次”的数的k进制表示；
所以，将eo的k进制表示转化为十进制，即为最终结果。

  public int singleNumber(int[] nums) {
         return onceNum(nums,3);
     }
     public int onceNum(int[] nums, int k){
         int[] eo = new int[32];
         for(int i=0;i!=nums.length;i++){
             setExclusiveOr(eo,nums[i],k);
         }
         return getNumFromKSysNum(eo,k);
     }
     public void setExclusiveOr(int[] eo, int value, int k){
         int[] valueK = getKSysNumFromNum(value,k);
         for(int i=0;i<eo.length;i++){
             eo[i]=((eo[i]+valueK[i])%k); //先求和再取余，等于，先取余再求和
         }
     }
     public int[] getKSysNumFromNum(int num,int k){
         int[] res = new int[32];
         for(int i=0;i<32;i++){
             res[i]=(num%k); // 0位是最低位
             num/=k;
         }
         return res;
     }
     public int getNumFromKSysNum(int[] num,int k){
         int res=0;
         for(int i=0;i<32;i++){
             res = k*res+num[31-i];

         }
         return res;
     }

注：中间转成k进制的函数也可以写成下面的形式

 public int[] getKSysNumFromNum(int num,int k){
         int[] res = new int[32];
         int i=0;
         while(num!=0){
             res[i++]=(num%k); // 0位是最低位
             num/=k;
         }
         return res;
     }