题目（回忆版）：

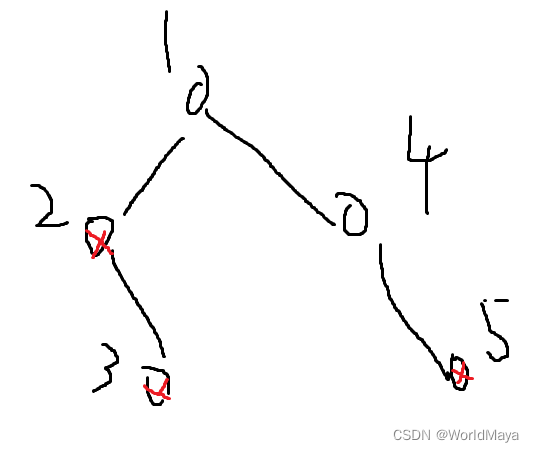
给一棵树，每个节点要么是白色要么是红色，并且有节点编号，要求查询每个节点所在子树中红色节点的数量。
先是一个正整数 n，表示树有 n 个节点。
第二行给出 n-1 个数字，表示从2号节点开始每个节点的父节点编号。
第三行给出长度为 n 的字符串，表示从1号节点开始每个节点的颜色（W白色/R红色）。
接下来是一个正整数 q，表示有 q 次查询。
然后是 q 行，每行一个正整数，对应一个节点的编号，要求输出这个编号节点所在子树中红色节点的数量。

例一：

输入：
5
1 2 1 4
WRRWR
5
1
2
3
4
5
输出：
3
2
1
1
1

解题思路：

构建节点：节点中存储节点颜色和它的子节点们的编号。
存储节点：用一个编号与节点对象对应的 map 存储编号及对应的节点。
搜索节点：以节点编号在 map 中读取节点，根据节点内部存储的子节点编号在 map 中向下搜索子节点。
查询子树红色节点数量：深度优先搜索（类比二叉树后序遍历），统计红色子节点的数量，并将每个节点编号对应的红色子节点数记录在哈希表 h 中，之后每次查询都从哈希表 h 中直接查询即可。

代码：

#include <iostream>
#include <vector>
#include <string>
#include <map>
using namespace std;
struct TreeNode {
    int id;  // 节点编号
    char c;  // 节点颜色（W白色/R红色）
    vector<int> sub;  // 子节点编号
    TreeNode() {}
    TreeNode(int x, char y) : id(x), c(y) {}
};
map<int, TreeNode> m;  // 用于存储节点信息（编号，节点）
map<int, int> h;  // 用于存储节点的红色子节点数（节点编号，红色子节点数）
int dfs(TreeNode* root) {  // 搜索一个节点的红色子节点数
    if(root == nullptr) return 0;
    int sum = 0;
    int size = root->sub.size();
    for(int i = 0; i < size; i++) {
        sum += dfs(&m[root->sub[i]]);  // 递归搜索所有的子节点
    }
    sum += (root->c == 'R') ? 1 : 0;  // 如果当前节点是红色，则红色子节点数加一
    h[root->id] = sum;  // 将当前节点的红色子节点数存入map
    return sum;  // 向父节点传递当前节点的红色子节点数
}

int main() {
    int n;
    while (cin >> n) {
        vector<int> a(n, 0);  // 从2号节点开始，每个节点的父节点编号
        string s;  // 每个节点的颜色（按节点编号顺序）
        for(int i = 1; i < n; i++) {
            cin >> a[i];
        }
        cin >> s;
        m.clear();
        TreeNode n1(1, s[0]);  // 根节点
        m.emplace(1, n1);  // 将根节点存入map的第一个位置
        for(int i = 1; i < n; i++) {
            TreeNode temp(i + 1, s[i]);  // 创建第i+1号节点
            m.emplace(i + 1, temp);
            m[a[i]].sub.emplace_back(i + 1);  // 将第i+1号节点存入其父节点的子节点集合中
        }
        h.clear();
        dfs(&m[1]);  // 从根节点开始完成搜索一次，即可得到所有节点的红色子节点数，存入h表，后续查询的时间复杂度都是O(1)
        int q;
        cin >> q;
        while(q--) {  // q次查询
            int t;
            cin >> t;
            cout << h[t] << endl;
        }
    }
}