需求描述:
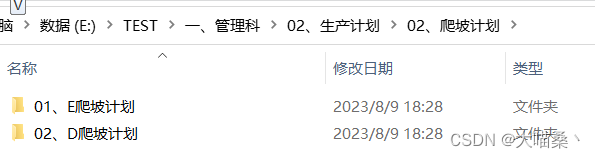
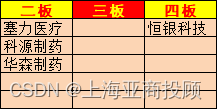
需要将以下excel内的结构解析,并创建对应的文件目录
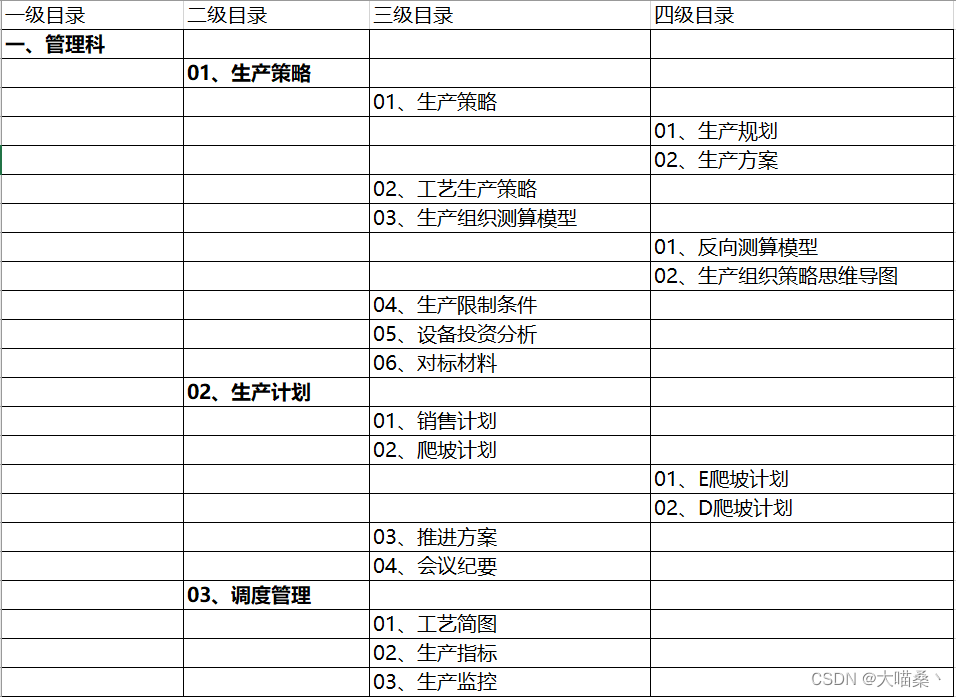
实现思路:
实现思路是通过解析Excel文件中的目录结构,并根据目录结构创建对应的文件夹。
具体的实现步骤如下:
1. 加载指定的Excel文件,获取活动的工作表。
2. 创建一个空的目录栈列表,用于记录当前每一级目录。
3. 遍历工作表中的每一行,从第2行开始。
4. 对于每一行,获取当前行的目录级别。
5. 遍历当前行的每一个单元格,判断是否是目录名。
6. 如果单元格的值不为None且不为"@",则将其作为目录名进行处理。
7. 清空目录栈中当前行级别及以下的目录,以保持目录栈的正确层级关系。
8. 将当前目录名加入目录栈。
9. 根据目录栈中的目录名构建完整的目录路径。
10. 使用函数创建目录,如果目录已存在则忽略。
11. 重复步骤3至步骤10,直到遍历完所有行。
12. 完成目录的创建。
那么,怎么去理解目录栈呢?
当我们遍历Excel文件的每一行时,我们需要记录当前的目录结构。目录栈就像是一个容器,用来存储目录的层级关系。
假设Excel文件中的目录结构是这样的:
目录A
目录B
目录C
目录D
目录E
目录F
我们可以使用一个列表来表示目录栈,开始时是一个空列表 []。
当我们遍历到第一行时,目录栈为空,我们将目录A加入目录栈中,目录栈变为 ['目录A']。
当我们遍历到第二行时,目录栈中已经有了目录A,我们需要将目录B加入目录栈中,所以目录栈变为 ['目录A', '目录B']。
当我们遍历到第三行时,目录栈中已经有了目录A和目录B,我们需要将目录C加入目录栈中,所以目录栈变为 ['目录A', '目录B', '目录C']。
当我们遍历到第四行时,目录栈中已经有了目录A,我们需要将目录D加入目录栈中,但同时我们需要清空目录栈中目录B和目录C以下的内容,所以目录栈变为 ['目录A', '目录D']。
当我们遍历到第五行时,目录栈中已经有了目录A和目录D,我们需要将目录E加入目录栈中,所以目录栈变为 ['目录A', '目录D', '目录E']。
当我们遍历到第六行时,目录栈中已经有了目录A、目录D和目录E,我们需要将目录F加入目录栈中,所以目录栈变为 ['目录A', '目录D', '目录E', '目录F']。
通过这样的方式,我们使用列表来模拟目录栈的结构,每当遍历到一个新的目录时,我们将其加入目录栈中,并且可以根据需要清空目录栈中的部分内容,以保持正确的目录层级关系。
实现代码:
import openpyxl
import os
def parse_excel(file_path):
workbook = openpyxl.load_workbook(file_path)
sheet = workbook.active
directory_stack = [] # 用于记录当前每一级目录的栈
for row in sheet.iter_rows(min_row=2, values_only=True):
level = len(directory_stack) # 当前行的目录级别
for i, cell_value in enumerate(row):
if cell_value is not None and cell_value != "@":
directory_stack = directory_stack[:i] # 清空目录栈中当前行级别及以下的目录
directory_stack.append(cell_value) # 将当前目录加入目录栈
directory_path = "\\".join(directory_stack) # 构建完整的目录路径
full_path = file_path.replace(os.path.basename(file_path), "") + directory_path
os.makedirs(full_path, exist_ok=True) # 创建目录,如果目录已存在则忽略
parse_excel("E:\TEST\文件.xlsx")
代码逻辑:
当我们调用 parse_excel(“E:\TEST\文件.xlsx”) 时,会执行 parse_excel 函数。
在 parse_excel 函数中,首先通过 openpyxl.load_workbook(file_path) 加载指定的 Excel 文件,并将其赋值给 workbook 变量。
然后,通过 workbook.active 获取活动的工作表,并将其赋值给 sheet 变量。
接下来,我们创建一个空列表 directory_stack,用于记录当前每一级目录的栈。
然后,通过遍历 sheet 中的每一行(从第2行开始),我们逐行解析 Excel 文件中的目录结构。
对于每一行,我们首先获取当前行的目录级别,即目录栈 directory_stack 的长度。
然后,我们遍历当前行的每一个单元格,判断单元格的值是否不为 None 且不为 “@”。
如果满足条件,说明该单元格是一个目录名,我们需要对目录栈进行相应的操作。
首先,我们使用 directory_stack = directory_stack[:i] 清空目录栈中当前行级别及以下的目录,这样就保证目录栈中只保留了当前行级别之前的目录。
然后,我们将当前目录加入目录栈,使用 directory_stack.append(cell_value)。
接着,我们根据目录栈中的目录名,构建完整的目录路径。
通过 “\”.join(directory_stack),我们使用反斜杠将目录栈中的目录名连接起来,得到一个完整的目录路径。
最后,我们使用 os.makedirs(full_path, exist_ok=True) 创建目录,如果目录已存在则忽略。
通过这样的逻辑,我们可以根据 Excel 文件中的目录结构,逐行解析并创建对应的文件夹。每一行代表一个目录,每一列代表目录的级别。代码会根据目录的层级关系,构建目录栈,并根据目录栈构建完整的目录路径,最终使用 os.makedirs 函数创建目录。
最终效果图(部分):