一、购物篮分析简介

相信，很多人都听过沃尔玛购物篮分析的故事---“啤酒和尿布湿“，即分析购买尿布湿的顾客最喜欢购买的商品是什么？（啤酒）。在零售终端经营中，通过购物篮分析，分析不同商品之间销售的关联性，对于零售终端的商品布局摆放，有着非常重要的意义。下面就介绍一下，在Power BI中如何完成购物篮分析。

二、数据源表

两张数据源表，一张《销售单据》，一张《商品表》，如下图

表《销售单据》

流水单号	商品	数量	价格	金额
A0001	中华	1	45	45
A0002	中华	2	45	90
A0002	脉动	1	5	5
A0003	中华	1	45	45
A0003	脉动	2	5	10
A0003	打火机	1	1	1
A0004	奥利奥	1	10	10
A0004	脉动	1	5	5
A0004	打火机	1	1	1
A0004	口香糖	1	5	5

表《商品表》

商品

中华

脉动

打火机

奥利奥

口香糖

三、数据分析过程

步骤一、获取数据

1、将两张表添加到Power BI中，并将《商品表》，重新命名为《商品表(A)》

步骤二、建立关系

1、通过复制《商品表(A)》，新建一张表，并命名为《商品表(B)》

   商品表(B)=’商品表(A)’

2、在“模型视图”中，《商品表(A)》通过字段“商品”与《销售单据》建立1对多的关系（实线）；《商品表(B)》通过字段“商品”与《销售单据》建立1对多的关系，但是此关系状态设置为未激活（虚线）。

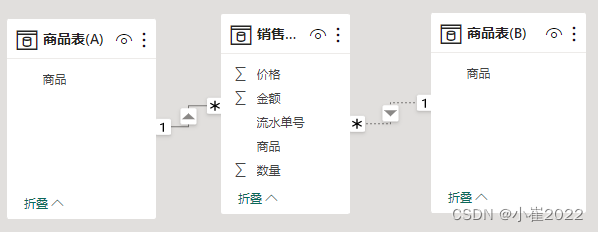
步骤三、创建可视化对象

1、在“报表视图”中创建可视化对象---矩阵，并将《商品表(A)》中的“商品”设置为行，重命名为“商品A”。

2、创建可视化对象---切片器，并将《商品表(B)》中的“商品”设置为字段，重命名为“商品B”。

步骤四、创建度量值

1、新建度量值---客户数量

  客户数量 = DISTINCTCOUNTNOBLANK('销售单据'[流水单号])

  将“客户数量”设置为矩阵的值，矩阵中则显示出购买不同商品A的客户数量。

2、新建度量值---购买商品B的客户数量

购买商品B的客户数量 =

 // 取消《商品表(A)》的筛选功能，激活《商品表(B)》和《销售单据》之间的1对多关系，进而统计出购买商品B的客户数量

 VAR table1=CALCULATETABLE(VALUES('销售单据'[流水单号]),USERELATIONSHIP('商品表(B)'[商品],'销售单据'[商品]),ALL('商品表(A)'))

 VAR result1=CALCULATE('度量值表'[客户数量],table1)

 // 如果显示为空，则客户数量显示为0

 VAR result2=IF(ISBLANK(result1),0,result1)

 // 如果矩阵中行值(商品A）与切片器-商品B中勾选的商品相同，则客户数量显示为空

 VAR result=IF(SELECTEDVALUE('商品表(A)'[商品])=SELECTEDVALUE('商品表(B)'[商品]),BLANK(),result2)

 RETURN result

3、将度量值“购买商品B的客户数量”设置为矩阵的值，并重命名为“同时购买商品B的客户数量。

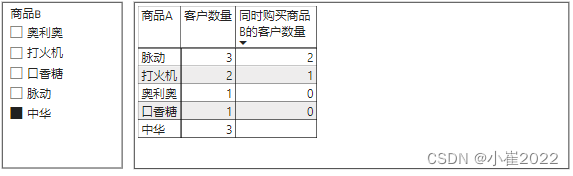
如果单独看度量值“购买商品B的客户数量”，它统计显示就只是购买商品B的客户数量，但是将其放入矩阵后，受到矩阵行（商品A）值的筛选影响，显示的就是购买商品A

同时购买了商品B的客户数量。如，将切片器-商品B中勾选“中华“，矩阵中第一行显示的就是购买商品A-脉动的客户数量为3个，其中有2个同时购买了商品B-中华。（矩阵中”同时购买商品B的客户数量按降序排列）

4、新建度量值---客户占比

客户占比 = DIVIDE('度量值表'[购买商品B的客户数量],'度量值表'[客户数量])

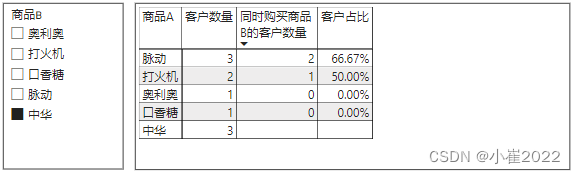
即购买了商品A同时购买商品B的客户占比。

5、将度量值“客户占比”设置为矩阵的值

6、新建度量值---购买商品B的金额

购买商品B的金额 =

// 取消《商品表(A)》的筛选功能，激活《商品表(B)》和《销售单据》之间的1对多关系，进而统计出购买商品B的金额

CALCULATE(SUM('销售单据'[金额]),USERELATIONSHIP('商品表(B)'[商品],'销售单据'[商品]),ALL('商品表(A)'))

7、新建度量值---同时购买商品B的金额

同时购买商品B的金额 =

 // 统计筛选出购买商品A的流水单号

 VAR tableA=CALCULATETABLE(VALUES('销售单据'[流水单号]))

 //  取消《商品表(A)》的筛选功能，激活《商品表(B)》和《销售单据》之间的1对多关系，进而统计出购买商品B的流水单号

 VAR tableB=CALCULATETABLE(VALUES('销售单据'[流水单号]),USERELATIONSHIP('商品表(B)'[商品],'销售单据'[商品]),ALL('商品表(A)'))

 // 购买商品A的流水单号与购买商品B的流水单号的交集，即为同时购买了商品A和商品B的流水单号，或者说是够买了商品A同时购买了商品B的流水单号

 VAR AandB=NATURALINNERJOIN(tableA,tableB)

 // 根据同时购买了商品A和商品B的流水单号，统计出同时购买商品B的金额

 VAR result=CALCULATE('度量值表'[购买商品B的金额],AandB)

 RETURN result

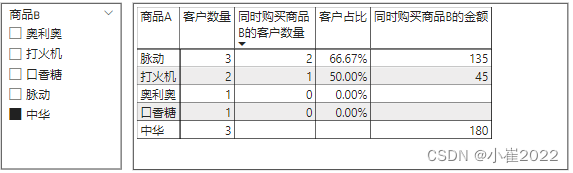
8、将度量值“同时购买商品B的金额” 设置为矩阵的值

在切片器-商品B中勾选“中华”，矩阵中显示商品A-脉动的客户数量为3个，其中有2个购买了商品B-中华，客户占比66.67%，同时购买商品B的金额为135。

步骤五、可视化图表优化

1、当切片器-商品B中勾选了某个商品比如“中华”，在矩阵商品A下方就不再显示该商品“中华”

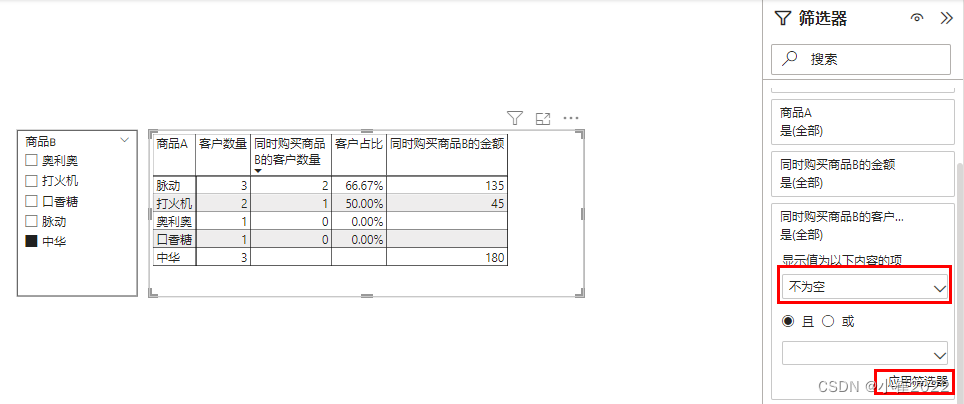
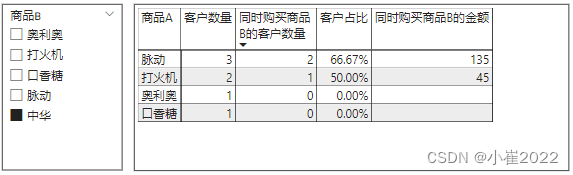
选中可视化对象矩阵，打开“筛选器”对话框，在“同时购买商品B的客户数量”下方，将“显示值为以下内容的项”设置为“不为空”，点击右下角“应用筛选器”。最终效果显示如下