图常见的遍历方式有两种，一种是宽度优先遍历，一种是深度优先遍历。

宽度优先遍历
宽度优先遍历和之前介绍的二叉树的层级遍历类似，主要也是利用Queue来完成层级的遍历，除此之外，因为图中很可能有环，所以还需要一个Set集合来保证遍历的过程中没有重复的点打印，防止死循环。
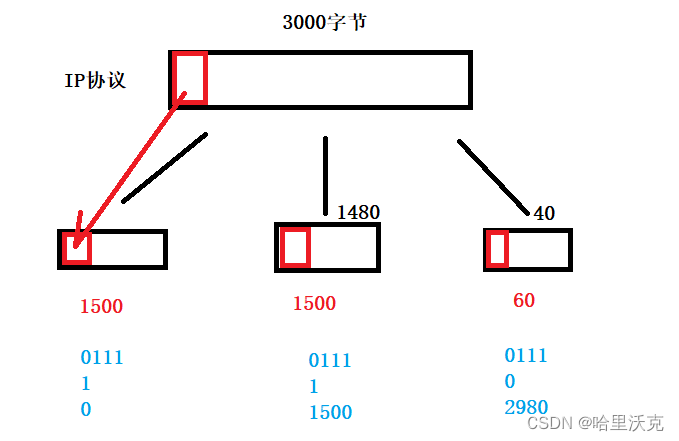
比如说，图形结构如下图所示：

遍历时，先遍历a，将a放入队列，弹出后，a直接到达的节点的有b和c，将b,c放入队列，b弹出时，直接到达的节点有c和p。
如果此时再将c放入队列那c就会遍历两次，根据set集合判断放入p，遍历完c,p后，p直接到达的点是a，如果没有set集合，那么就死循环了。在a处重新开始遍历。

BFS
需要注意的是，一定要给一个开始的节点node。并且出堆就打印。

public class BFS {

    public static void bfs(Node node) {
        if (node == null) {
            return;
        }

        Queue<Node> heap = new LinkedList<>();
        Set<Node> set = new HashSet<>();
        heap.add(node);
        set.add(node);
        while (!heap.isEmpty()) {
            Node cur = heap.poll();
            System.out.print(cur.value + " ");
            for (Node next : cur.nexts) {
                if (!set.contains(next)) {
                    heap.add(next);
                    set.add(next);
                }
            }
        }
    }
}

深度优先遍历
深度优先遍历的技巧就在于一条道走到黑，只要下面还有，就一直先向下找，同样需要set集合来去重，避免死循环。进栈就打印。

DFS

内层for循环中，与BFS有所区别，利用set去重做判断，如果不存在则将当前Node和next的Node都放入Stack中，然后break。注意要先将当前Node放入栈中，因为后进先出，都放入后，栈中会保留你遍历的路径，break再次弹出的是第一次放入的next的Node。下次会从next的Node向下遍历，看是否在set中存在。

public class DFS {

    public static void dfs(Node node){
        if (node == null){
            return;
        }
        Stack<Node> stack = new Stack<>();
        Set<Node> set = new HashSet<>();
        stack.add(node);
        set.add(node);
        System.out.println(node.value + " ");
        while (!stack.isEmpty()){
            Node cur = stack.pop();
            for (Node next : cur.nexts){
                if (!set.contains(next)){
                    stack.add(cur);
                    stack.add(next);
                    set.add(next);
                    System.out.println(next.value + " ");
                    break;
                }
            }
        }
    }
}