0-1背包问题

问题描述：有n件物品和一个最多能背重量为w 的背包。第i件物品的重量是weight[i]，得到的价值是value[i] 。每件物品只能用一次，求解将哪些物品装入背包里物品价值总和最大。

二维数组解法

动态规划五部曲：

1. 确定dp数组以及下标的含义
   对于背包问题，有一种写法， 是使用二维数组，即dp[i][j] 表示从下标为[0-i]的物品里任意取，放进容量为j的背包，价值总和最大是多少。
   
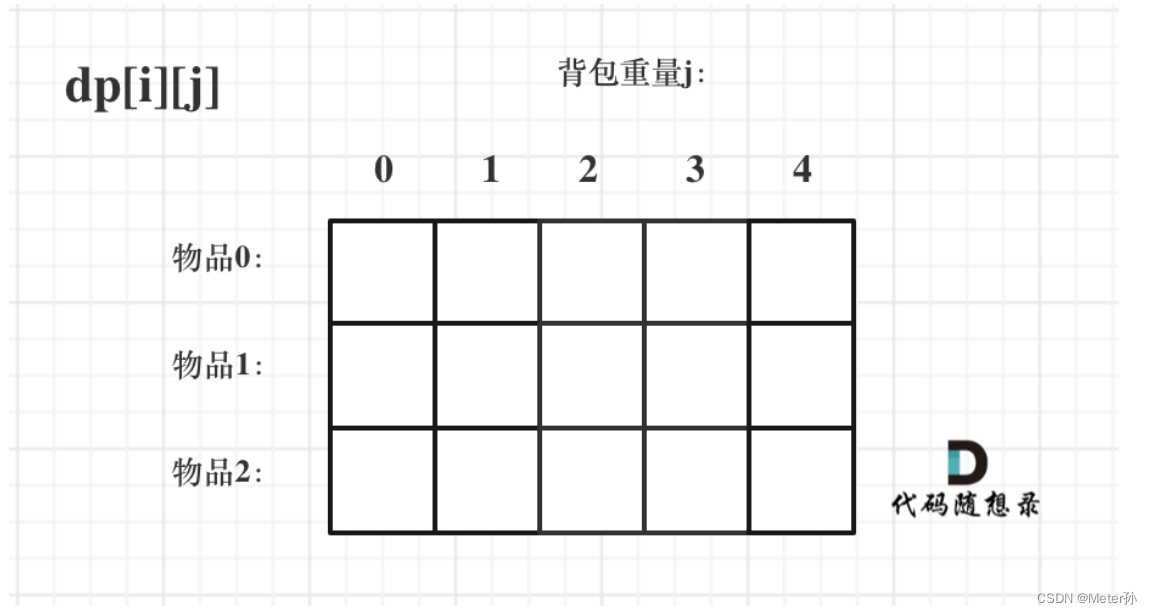
2. 确定递推公式
   可以有两个方向推出来dp[i][j]：

• 不放物品i：由dp[i - 1][j]推出，即背包容量为j，里面不放物品i的最大价值，此时dp[i][j]就是dp[i - 1][j]。(其实就是当物品i的重量大于背包j的重量时，物品i无法放进背包中，所以背包内的价值依然和前面相同。)
• 放物品i：由dp[i - 1][j - weight[i]]推出，dp[i - 1][j - weight[i]] 为背包容量为j - weight[i]的时候不放物品i的最大价值，那么dp[i - 1][j - weight[i]] + value[i] （物品i的价值），就是背包放物品i得到的最大价值

3. dp数组如何初始化
   首先从dp[i][j]的定义出发，如果背包容量j为0的话，即dp[i][0]，无论是选取哪些物品，背包价值总和一定为0。
   状态转移方程 dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]); 可以看出i 是由 i-1 推导出来，那么i为0的时候就一定要初始化。
   dp[0][j]，即：i为0，存放编号0的物品的时候，各个容量的背包所能存放的最大价值。
   那么很明显当 j < weight[0]的时候，dp[0][j] 应该是 0，因为背包容量比编号0的物品重量还小。
   当j >= weight[0]时，dp[0][j] 应该是value[0]，因为背包容量放足够放编号0物品。
4. 确定遍历顺序
   有两个遍历的维度：物品与背包重量，先遍历哪一个都可以
   5.检查

function testWeightBagProblem (weight, value, size) {
    // 定义 dp 数组
    const len = weight.length,
          dp = Array(len).fill().map(() => Array(size + 1).fill(0));

    // 初始化
    for(let j = weight[0]; j <= size; j++) {
        dp[0][j] = value[0];
    }

    // weight 数组的长度len 就是物品个数
    for(let i = 1; i < len; i++) { // 遍历物品
        for(let j = 0; j <= size; j++) { // 遍历背包容量
            if(j < weight[i]) dp[i][j] = dp[i - 1][j];
            else dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
        }
    }

    console.table(dp)

    return dp[len - 1][size];
}

一维数组解法

在使用二维数组的时候，递推公式：dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
其实可以发现如果把dp[i - 1]那一层拷贝到dp[i]上，表达式完全可以是：dp[i][j] = max(dp[i][j], dp[i][j - weight[i]] + value[i]);
与其把dp[i - 1]这一层拷贝到dp[i]上，不如只用一个一维数组了，只用dp[j]

1. 在一维dp数组中，dp[j]表示：容量为j的背包，所背的物品价值可以最大为dp[j]。
2. 此时dp[j]有两个选择，一个是取自己dp[j] 相当于 二维dp数组中的dp[i-1][j]，即不放物品i，一个是取dp[j - weight[i]] + value[i]，即放物品i，指定是取最大的，毕竟是求最大价值。
3. dp[j]表示：容量为j的背包，所背的物品价值可以最大为dp[j]，那么dp[0]就应该是0，因为背包容量为0所背的物品的最大价值就是0。
4. 二维dp遍历的时候，背包容量是从小到大，而一维dp遍历的时候，背包是从大到小。
   倒序遍历是为了保证物品i只被放入一次！。但如果一旦正序遍历了，那么物品0就会被重复加入多次！
   所以从后往前循环，每次取得状态不会和之前取得状态重合，这样每种物品就只取一次了。
   要先遍历物品。因为一维dp的写法，背包容量一定是要倒序遍历（原因上面已经讲了），如果遍历背包容量放在上一层，那么每个dp[j]就只会放入一个物品，即：背包里只放入了一个物品。
5. 检查

function testWeightBagProblem(wight, value, size) {
  const len = wight.length, 
    dp = Array(size + 1).fill(0);
  for(let i = 1; i <= len; i++) {
    for(let j = size; j >= wight[i - 1]; j--) {
      dp[j] = Math.max(dp[j], value[i - 1] + dp[j - wight[i - 1]]);
    }
  }
  return dp[size];
}

416. 分割等和子集

本题要求集合里能否出现总和为 sum / 2 的子集。

1. 套到本题，dp[j]表示 背包总容量（所能装的总重量）是j，放进物品后，背的最大重量为dp[j]。
2. 本题，相当于背包里放入数值，那么物品i的重量是nums[i]，其价值也是nums[i]。dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]);
3. 如果题目给的价值都是正整数那么非0下标都初始化为0就可以了，如果题目给的价值有负数，那么非0下标就要初始化为负无穷。这样才能让dp数组在递推的过程中取得最大的价值，而不是被初始值覆盖了。
4. 如果使用一维dp数组，物品遍历的for循环放在外层，遍历背包的for循环放在内层，且内层for循环倒序遍历！
5. 检查

var canPartition = function(nums) {
    const sum = (nums.reduce((p, v) => p + v));
    if (sum & 1) return false;
    const dp = Array(sum / 2 + 1).fill(0);
    for(let i = 0; i < nums.length; i++) {
        for(let j = sum / 2; j >= nums[i]; j--) {
            dp[j] = Math.max(dp[j], dp[j - nums[i]] + nums[i]);
            if (dp[j] === sum / 2) {
                return true;
            }
        }
    }
    return dp[sum / 2] === sum / 2;
};