题目描述 

输入 #1
3 13
1 1 -1 -1 1 -1 1 1 1 -1 1 1 1
1 -1 1 -1 1 -1 1 -1 1 -1 -1 1 -1
1 -1 -1 1 1 -1 1 1 1 -1 1 1 1 输出 #1
24输入 #2
3 13
-1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1输出 #2
-20 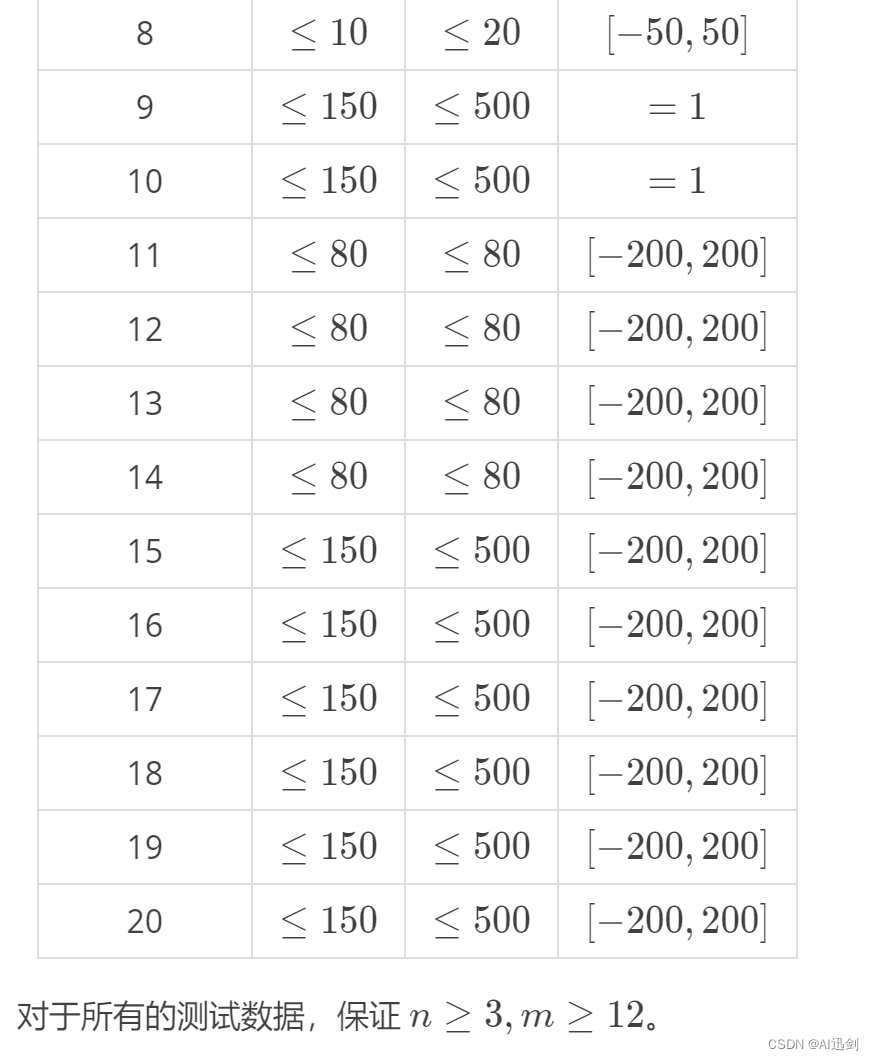
解析与代码







#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
#define MAXN 150
#define MAXM 500
#define INF 0x3fffffff
int a[MAXN+10][MAXM+10],n,m,blk[MAXM+10][2],f[2][10][MAXN+10][MAXN+10],s[MAXN+10][MAXM+10],tmp[MAXN+10][MAXN+10],ans=-INF;
void Read(int &x){
static char c;
bool f(0);
while(c=getchar(),c!=EOF){
if(c=='-')
f=1;
else if(c>='0'&&c<='9'){
x=c-'0';
while(c=getchar(),c>='0'&&c<='9')
x=x*10+c-'0';
ungetc(c,stdin);
if(f)
x=-x;
return;
}
}
}
void read(){
Read(n),Read(m);
int i,j;
for(i=1;i<=n;i++)
for(j=1;j<=m;j++){
Read(a[i][j]);
s[i][j]=s[i-1][j]+a[i][j];
}
}
void dp(){
int i,j,k;
memset(f[1],0xb0,sizeof f[1]);
for(i=1;i<=n;i++)
for(j=i;j<=n;j++)
f[1][1][i][j]=s[j][1]-s[i-1][1];
blk[1][0]=blk[1][1]=-INF;
for(k=2;k<=m;k++){
memset(f[k&1],0xb0,sizeof f[k&1]);
//N的第一部分
for(i=1;i<=n;i++)
for(j=i;j<=n;j++)
f[k&1][1][i][j]=max(s[j][k]-s[i-1][k],f[(k&1)^1][1][i][j]+s[j][k]-s[i-1][k]);
//N的第二部分
for(i=1;i<=n;i++){
tmp[i][n+1]=-INF;
for(j=n;j>=i;j--)
tmp[i][j]=max(tmp[i][j+1],f[(k&1)^1][1][i][j]);
}
for(i=1;i<=n;i++)
for(j=i;j<=n;j++){
f[k&1][2][i][j]=max(f[k&1][2][i][j],tmp[i][j+1]+s[j][k]-s[i-1][k]);
tmp[i][j]=-INF;
}
for(i=1;i<=n;i++)
for(j=i;j<=n;j++)
tmp[j+1][j+1]=max(tmp[j+1][j+1],f[(k&1)^1][2][i][j]);
for(i=1;i<=n;i++)
for(j=i+1;j<=n;j++)
tmp[i][j]=max(tmp[i][j],tmp[i][j-1]);
for(i=1;i<=n;i++)
for(j=i;j<=n;j++)
f[k&1][2][i][j]=max(f[k&1][2][i][j],tmp[i][j]+s[j][k]-s[i-1][k]);
for(i=1;i<=n;i++)
for(j=i;j<=n;j++)
tmp[i][j]=f[(k&1)^1][2][i][j];
for(j=1;j<=n;j++)
for(i=1;i<j;i++)
tmp[i+1][j]=max(tmp[i+1][j],tmp[i][j]);
for(i=1;i<=n;i++)
for(j=i;j<n;j++)
tmp[i][j+1]=max(tmp[i][j+1],tmp[i][j]);
for(i=1;i<=n;i++)
for(j=i;j<=n;j++)
f[k&1][2][i][j]=max(f[k&1][2][i][j],tmp[i][j]+s[j][k]-s[i-1][k]);
//N的第三部分
for(i=1;i<=n;i++)
for(j=i;j<=n;j++)
tmp[i][j]=f[(k&1)^1][2][i][j];
for(j=1;j<=n;j++)
for(i=j;i>1;i--)
tmp[i-1][j]=max(tmp[i-1][j],tmp[i][j]);
for(i=1;i<=n;i++)
for(j=i+1;j<=n;j++)
f[k&1][3][i][j]=max(f[k&1][3][i][j],max(tmp[i+1][j],f[(k&1)^1][3][i][j])+s[j][k]-s[i-1][k]);
//NO之间空白
blk[k][0]=blk[k-1][0];
for(i=1;i<=n;i++)
for(j=i;j<=n;j++)
blk[k][0]=max(blk[k][0],f[(k&1)^1][3][i][j]);
//O的第一部分
for(i=1;i<=n;i++)
for(j=i+2;j<=n;j++)
f[k&1][4][i][j]=blk[k-1][0]+s[j][k]-s[i-1][k];
//O的第二部分
for(i=1;i<=n;i++)
for(j=i+2;j<=n;j++)
f[k&1][5][i][j]=max(f[(k&1)^1][4][i][j],f[(k&1)^1][5][i][j])+a[i][k]+a[j][k];
//O的第三部分
for(i=1;i<=n;i++)
for(j=i+2;j<=n;j++)
f[k&1][6][i][j]=f[(k&1)^1][5][i][j]+s[j][k]-s[i-1][k];
//OI之间空白
blk[k][1]=blk[k-1][1];
for(i=1;i<=n;i++)
for(j=i;j<=n;j++)
blk[k][1]=max(blk[k][1],f[(k&1)^1][6][i][j]);
//I的第一部分
for(i=1;i<=n;i++)
for(j=i+2;j<=n;j++)
f[k&1][7][i][j]=max(blk[k-1][1],f[(k&1)^1][7][i][j])+a[i][k]+a[j][k];
//I的第二部分
for(i=1;i<=n;i++)
for(j=i+2;j<=n;j++)
f[k&1][8][i][j]=max(f[(k&1)^1][7][i][j],f[(k&1)^1][8][i][j])+s[j][k]-s[i-1][k];
//I的第三部分
for(i=1;i<=n;i++)
for(j=i+2;j<=n;j++){
f[k&1][9][i][j]=max(f[(k&1)^1][8][i][j],f[(k&1)^1][9][i][j])+a[i][k]+a[j][k];
ans=max(ans,f[k&1][9][i][j]);
}
}
}
int main()
{
read();
dp();
printf("%d\n",ans);
} 谢谢观看,希望对您有帮助![]()