文章目录
- 栈求解迷宫路径
- 1. 求解迷宫思想和难点
- 2. 定义迷宫
- 3. 定义方向结构体和数组
- 4. 迷宫路径穷举
- 5. 代码总测试
栈求解迷宫路径
本文分为两部分,第一部分让大家整体了解栈求解迷宫路径的整体思路和算法实现,第二部分仔细分析迷宫求解过程。小白门看不懂第一部分没关系,可以直接跳到下一部分,从定义迷宫开始往后看。
1. 求解迷宫思想和难点
求解迷宫路径整体思路就是穷举所有路径。从点出发,按某一方向探索,沿途在经过的位置设下标记。若能走通即某处可以到达。若该点所有方向均没有通路,则原返回,直到有路可走。如此循环直到到达终点,或无路可走返回起点。求解过程会用一个栈path存储迷宫路径上的所有有效坐标。
求解开始时,path栈首先存储起点坐标,此时栈顶就是起点坐标。内部循环,不断根据栈顶坐标(也就是当前坐标)和迷宫图得到下一步行走方向。
- 有路可走则将下一个坐标入栈作为当前坐标,进入下一个循环。
- 如果无路可走则出栈返回前一个结点,换方向尝试
求解迷宫穷举路径的难点就在于,如何在原路返回前一个点查找路径时不会重复的到达某点,形成死循环?
- 方案一是另外设置一标志数组 flag[n],其所有元素都初始化为0,一旦到达了某点(ij)之后,将对应flag]置1,下次再试探该位置时,因为已经置1了,就不能再选它了;缺点时有些浪费空间了撒
- 方案二是当到达某点
(i,j)后将对应maze[i][j]置-1,其他未到达过的点其值只能是1或0,可与未到达过的点区别开来。这里采用方案二实现算法。
整体了解完迷宫求解算法,下面便是重点分析了
2. 定义迷宫

如上图,对于长M,宽N的迷宫,需要在迷宫周围围上墙。所以定义的迷宫,我们用二级指针maze来表示迷宫,对应的为 mazeSample[M + 2][N + 2],整个迷宫图内部0标识通路,1表示围墙。
//定义迷宫数组的长宽M,N
const int M = 8;
const int N = 8;
//定义并初始化迷宫二维数组
int mazeSample[M + 2][N + 2] =
{
{1,1,1,1,1,1,1,1,1,1},
{1,0,0,1,0,0,0,1,0,1},
{1,0,0,1,0,0,0,1,0,1},
{1,0,0,0,0,1,1,0,0,1},
{1,0,1,1,1,0,0,0,0,1},
{1,0,0,0,1,0,0,0,0,1},
{1,0,1,0,0,0,1,0,0,1},
{1,0,1,1,1,0,1,1,0,1},
{1,1,0,0,0,0,0,0,0,1},
{1,1,1,1,1,1,1,1,1,1}
};
int** maze = (int**)malloc(sizeof(int*) * (M+2));
for (int i = 0; i < M+2; i++)
{
maze[i] = (int*)malloc(sizeof(int) * (N+2));
}
for (int i = 0; i < M+2; i++)
{
for (int j = 0; j < N+2; j++)
{
maze[i][j] = mazeSample[i][j];
}
}
//输出迷宫
for (int i = 0; i < M+2; i++)
{
for (int j = 0; j < N+2; j++)
{
cout << maze[i][j]<<" ";
}
cout << endl;
}

3. 定义方向结构体和数组
定义direct数组,数组元素为Direction结构体。Direction结构体存储两个整型变量,incX和intY分别表示该方向xy方向的增量。
当前坐标cur为:(x,y)
cur下一步移动的方向为:direct[v]
下一步的坐标next为:(x+direct[v].incX,y+direct[v].incY)
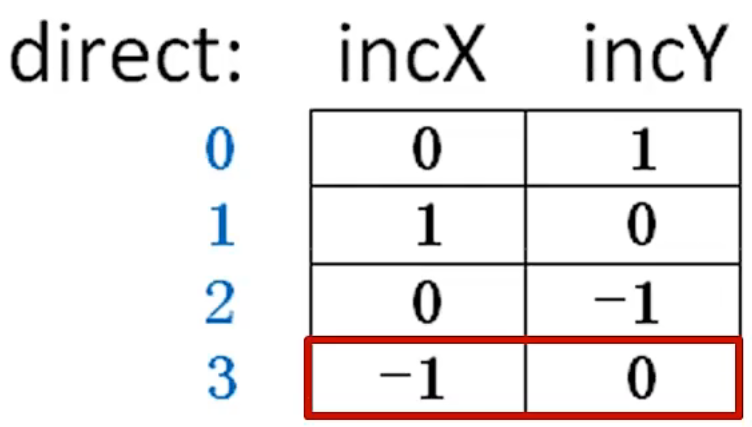
上图中数组从上往下分别对应下右上左四个方向
//定义方向结构体
struct Direction
{
//incX和intY分别表示该方向xy方向的增量
int incX, incY;
};
//共四个方向,定义存储四个结构体的数组
Direction direct[4] = { {0,1},{1,0},{0,-1},{-1,0} };
//定义点坐标
struct pointer{
int x;
int y;
};
4. 迷宫路径穷举
路径存储在pointer类型的storage栈中。
迷宫路径穷举函数findPath的实现思路是:将起点压入栈storage中,不断根据getDirection函数寻找下一个合适的坐标,并将坐标压入栈中,再将其迷宫对应数值设为-1,防止重复穷举路径。如果没有合适坐标,说明当前是死胡同,则出栈,在前一个坐标寻找新路径。具体如下:
//根据当前结点获得下一步方向,返回整数temp,对应direct[temp]即为方向。若返回值则说明无路可走为
int getDirection(int** maze, pointer cur)
{
int index = 0;
while (index < 4)
{
//判断迷宫中direct[index]对应的方向是否可以走,可以则返回index作为下一步方向标识
if (cur.x + direct[index].incX<N+1
&& cur.y + direct[index].incY<M+1
&&maze[cur.x + direct[index].incX][cur.y + direct[index].incY] == 0)return index;
index++;
}
return 4;
}
//求解迷宫的函数,如果迷宫有解,就返回true。如果没解就返回false
bool findPath(int** maze, stack<pointer>& s)
{
pointer cur;
cur.x = 1;
cur.y = 1;//cur就是起点
maze[cur.x][cur.y] = -1;//将到过的位置设置为-1,防止重复穷举
s.push( cur);
while (!s.empty())
{
pointer top = s.top();
if (top.x == 8 && top.y == 8)
{
return true;//判断是否是终点,是则成功并返回true
}
int direction = getDirection(maze,top);//根据栈顶拿到下一步方向direction
if (direction == 4)//direction == 4说明无路可走
{
s.pop();//无路可走出栈,根据前一个结点找新路径
}
else
{
top.x += direct[direction].incX;
top.y += direct[direction].incY;//根据方向更新当前坐标
maze[top.x][top.y] = -1;//将到过的位置设置为-1,防止重复穷举
s.push(top);
}
}
return false;
}
5. 代码总测试
输出路径对应的坐标(逆序,栈先进后出)

#include<iostream>
#include<Stack>
using namespace std;
//定义方向结构体
struct Direction
{
int incX, incY;
};
//定义存储四个结构体的数组,每个元素对应一个方向
Direction direct[4] = { {0,-1},{0,1},{-1,0},{1,0} };
//定义迷宫数组的长宽M,N
const int M = 8;
const int N = 8;
//迷宫中坐标
struct pointer
{
int x, y;//表示迷宫中位置的横纵坐标
};
//根据当前结点获得下一步方向,返回整数temp,对应direct[temp]即为方向。若返回值则说明无路可走为
int getDirection(int** maze, pointer cur)
{
int index = 0;
while (index < 4)
{
//判断迷宫中direct[index]对应的方向是否可以走,可以则返回index作为下一步方向标识
if (cur.x + direct[index].incX<N+1
&& cur.y + direct[index].incY<M+1
&&maze[cur.x + direct[index].incX][cur.y + direct[index].incY] == 0)return index;
index++;
}
return 4;
}
//求解迷宫的函数,如果迷宫有解,就返回true。如果没解就返回false
bool findPath(int** maze, stack<pointer>& s)
{
pointer cur;
cur.x = 1;
cur.y = 1;//cur就是起点
maze[cur.x][cur.y] = -1;//将到过的位置设置为-1,防止重复穷举
s.push( cur);
while (!s.empty())
{
pointer top = s.top();
if (top.x == 8 && top.y == 8)
{
return true;//判断是否是终点,是则成功并返回true
}
int direction = getDirection(maze,top);//根据栈顶拿到下一步方向direction
if (direction == 4)//direction == 4说明无路可走
{
s.pop();
}
else
{
top.x += direct[direction].incX;
top.y += direct[direction].incY;//根据方向更新当前坐标
maze[top.x][top.y] = -1;//将到过的位置设置为-1,防止重复穷举
s.push(top);
}
}
return false;
}
int main()
{
//定义并初始化迷宫二维数组
int mazeSample[M + 2][N + 2] =
{
{1,1,1,1,1,1,1,1,1,1},
{1,0,0,1,0,0,0,1,0,1},
{1,0,0,1,0,0,0,1,0,1},
{1,0,0,0,0,1,1,0,0,1},
{1,0,1,1,1,0,0,0,0,1},
{1,0,0,0,1,0,0,0,0,1},
{1,0,1,0,0,0,1,0,0,1},
{1,0,1,1,1,0,1,1,0,1},
{1,1,0,0,0,0,0,0,0,1},
{1,1,1,1,1,1,1,1,1,1}
};
int** maze = (int**)malloc(sizeof(int*) * (M+2));
for (int i = 0; i < M+2; i++)
{
maze[i] = (int*)malloc(sizeof(int) * (N+2));
}
for (int i = 0; i < M+2; i++)
{
for (int j = 0; j < N+2; j++)
{
maze[i][j] = mazeSample[i][j];
}
}
for (int i = 0; i < M+2; i++)
{
for (int j = 0; j < N+2; j++)
{
cout << maze[i][j]<<" ";
}
cout << endl;
}
stack<pointer> storage;
findPath(maze, storage);
cout << endl;
int num = 0;
while (!storage.empty())
{
pointer p = storage.top();
cout << "(" << p.x << "," << p.y << ")";
num++;
if (num % 4==0)cout << endl;
storage.pop();
}
}



![[附源码]Python计算机毕业设计SSM基于web动物园网站(程序+LW)](https://img-blog.csdnimg.cn/289ea437fe7341798cee0d6015a274c3.png)