提及机器学习框架与研究和工业的相关性。现在很少有项目不使用Google TensorFlow或Meta PyTorch，在于它们的可扩展性和灵活性。也就是说，花时间从头开始编码机器学习算法似乎违反直觉，即没有任何基本框架。然而，事实并非如此。自己对算法进行编码可以清晰而扎实地理解算法的工作原理以及模型真正在做什么。

      在本系列中，我们将学习如何仅使用普通和现代C++编写必须知道的深度学习算法，例如卷积、反向传播、激活函数、优化器、深度神经网络等。

        我们将通过学习一些现代 C++ 语言功能和相关编程细节来编码深度学习和机器学习模型，开始我们的故事之旅。

        查看其他故事：

1 — Coding 2D convolutions in C++

2 — Cost Functions using Lambdas

3 — Implementing Gradient Descent

4 — Activation Functions

...更多内容即将推出。

我无法创造的，我不明白。— 理查德·费曼

二、新式C++、 和 标头<algorithm><numeric>

        C++曾经是一种古老的语言，在过去十年中发生了翻天覆地的变化。主要变化之一是对函数式编程的支持。但是，还引入了其他几项改进，帮助我们开发更好、更快、更安全的机器学习代码。

        为了我们在这里的任务，C++ 和 标头中包含一组方便的通用例程。作为一个说明性的例子，我们可以通过以下方式获得两个向量的内积：<numeric><algorithm>

#include <numeric>
#include <iostream>

int main()
{
    std::vector<double> X {1., 2., 3., 4., 5., 6.};
    std::vector<double> Y {1., 1., 0., 1., 0., 1.};
 
    auto result = std::inner_product(X.begin(), X.end(), Y.begin(), 0.0);
    std::cout << "Inner product of X and Y is " << result << '\n';
    return 0;
}

并使用如下函数：accumulatereduce

std::vector<double> V {1., 2., 3., 4., 5.};

double sum = std::accumulate(V.begin(), V.end(), 0.0);

std::cout << "Summation of V is " << sum << '\n';

double product = std::accumulate(V.begin(), V.end(), 1.0, std::multiplies<double>());

std::cout << "Productory of V is " << product << '\n';

double reduction = std::reduce(V.begin(), V.end(), 1.0, std::multiplies<double>());

std::cout << "Reduction of V is " << reduction << '\n';

标头是大量有用的例程，例如,, , , ,等。让我们看一个说明性的例子：algorithmstd::transformstd::for_eachstd::countstd::uniquestd::sort

#include <algorithm>
#include <iostream>

double square(double x) {return x * x;}

int main() 
{
    std::vector<double> X {1., 2., 3., 4., 5., 6.};
    std::vector<double> Y(X.size(), 0);
 
    std::transform(X.begin(), X.end(), Y.begin(), square);
    std::for_each(Y.begin(), Y.end(), [](double y){std::cout << y << " ";});
    std::cout << "\n";
    
    return 0;
}

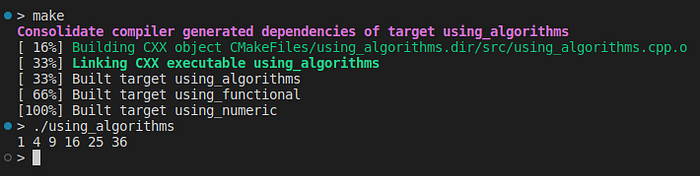
事实证明，在现代C++中，我们可以使用 、、 等函数，将函子、lambda 甚至香草函数作为参数传递，而不是显式使用 or 循环。forwhilestd::transformstd::for_eachstd::generate_n

上面的示例可以在 GitHub 上的此存储库中找到。

顺便说一下，是一个lambda。现在让我们谈谈函数式编程和lambda。[](double v){...}

三、函数式编程

        C++是一种多范式编程语言，这意味着我们可以使用它来创建使用不同“样式”的程序，例如OOP，过程式和最近的功能。

        对函数式编程的C++支持始于标头：<functional>

#include <algorithm> // std::for_each 
#include <functional> // std::less, std::less_equal, std::greater, std::greater_equal
#include <iostream> // std::cout

int main() 
{

    std::vector<std::function<bool(double, double)>> comparators 
    {
        std::less<double>(), 
        std::less_equal<double>(), 
        std::greater<double>(), 
        std::greater_equal<double>()
    };

    double x = 10.;
    double y = 10.;
    auto compare = [&x, &y](const std::function<bool(double, double)> &comparator)
    {
            bool b = comparator(x, y);
            std::cout << (b?"TRUE": "FALSE") << "\n";
    };

    std::for_each(comparators.begin(), comparators.end(), compare);

    return 0;
}

在这里，我们使用、、、和作为多态调用的示例，而不使用指针。std::functionstd::lessstd::less_equalstd::greaterstd::greater_equal

正如我们已经讨论过的，C++ 11 包括语言核心的更改以支持函数式编程。到目前为止，我们已经看到了其中之一：

auto compare = [&x, &y](const std::function<bool(double, double)> &comparator)
{
    bool b = comparator(x, y);
    std::cout << (b?"TRUE": "FALSE") << "\n";
};

此代码定义一个 lambda，一个 lambda 定义一个函数对象，即可调用对象。

请注意 ，这不是 lambda 名称，而是 lambda 分配到的变量的名称。事实上，lambda 是匿名对象。compare

此 lambda 由 3 个子句组成：捕获列表 （ ）、参数列表 （） 和正文（大括号之间的代码）。[&x, &y]const std::function<boll(double, double)> &comparator{...}

参数列表和 body 子句的工作方式与任何常规函数类似。捕获子句指定可在 lambda 主体中寻址的外部变量集。

Lambda 非常有用。我们可以像旧式函子一样声明和传递它们。例如，我们可以定义一个 L2 正则化 lambda：

auto L2 = [](const std::vector<double> &V)
{
    double p = 0.01;
    return std::inner_product(V.begin(), V.end(), V.begin(), 0.0) * p;
};

并将其作为参数传递回我们的层：

auto layer = new Layer::Dense();
layer.set_regularization(L2)

默认情况下，lambda 不会引起副作用，即它们不能更改外部内存空间中对象的状态。但是，如果需要，我们可以定义一个 lambda。考虑以下动量实现：mutable

#include <algorithm>
#include <iostream>

using vector = std::vector<double>;

int main() 
{

    auto momentum_optimizer = [V = vector()](const vector &gradient) mutable 
    {
        if (V.empty()) V.resize(gradient.size(), 0.);
        std::transform(V.begin(), V.end(), gradient.begin(), V.begin(), [](double v, double dx) 
        {
            double beta = 0.7;
            return v = beta * v + dx; 
        });
        return V;
    };

    auto print = [](double d) { std::cout << d << " "; };

    const vector current_grads {1., 0., 1., 1., 0., 1.};
    for (int i = 0; i < 3; ++i) 
    {
        vector weight_update = momentum_optimizer(current_grads);
        std::for_each(weight_update.begin(), weight_update.end(), print);
        std::cout << "\n";
    }

    return 0;
}

        每次调用都会产生不同的值，即使我们传递的值与参数相同。发生这种情况是因为我们使用关键字 .momentum_optimizer(current_grads)mutable

        对于我们现在的目的，函数式编程范式特别有价值。通过使用功能特性，我们将编写更少但更健壮的代码，更快地执行更复杂的任务。

四、矩阵和线性代数库

        好吧，当我说“纯C++”时，这并不完全正确。我们将使用可靠的线性代数库来实现我们的算法。

        矩阵和张量是机器学习算法的构建块。C++中没有内置矩阵实现（也不应该有）。幸运的是，有几个成熟且优秀的线性代数库可用，例如 Eigen 和 Armadillo。

        多年来，我一直在使用Eigen。Eigen（在Mozilla公共许可证2.0下）是仅标头的，不依赖于任何第三方库。因此，我将使用本征作为这个故事及以后的线性代数后端。

五、常见矩阵运算

最重要的矩阵运算是逐矩阵乘法：

#include <iostream>
#include <Eigen/Dense>

int main(int, char **) 
{
    Eigen::MatrixXd A(2, 2);
    A(0, 0) = 2.;
    A(1, 0) = -2.;
    A(0, 1) = 3.;
    A(1, 1) = 1.;

    Eigen::MatrixXd B(2, 3);
    B(0, 0) = 1.;
    B(1, 0) = 1.;
    B(0, 1) = 2.;
    B(1, 1) = 2.;
    B(0, 2) = -1.;
    B(1, 2) = 1.;

    auto C = A * B;

    std::cout << "A:\n" << A << std::endl;
    std::cout << "B:\n" << B << std::endl;
    std::cout << "C:\n" << C << std::endl;

    return 0;
}

        通常称为 ，此操作的计算复杂度为 O（N³）。由于广泛用于机器学习，我们的算法受到矩阵大小的强烈影响。mulmatmulmat

让我们谈谈另一种类型的逐矩阵乘法。有时，我们只需要系数矩阵乘法：

auto D = B.cwiseProduct(C);
std::cout << "coefficient-wise multiplication is:\n" << D << std::endl;

当然，在系数乘法中，参数的维度必须匹配。以同样的方式，我们可以添加或减去矩阵：

auto E = B + C;
std::cout << "The sum of B & C is:\n" << E << std::endl;

最后，让我们讨论三个非常重要的矩阵运算：、 和 ：transposeinversedeterminant

std::cout << "The transpose of B is:\n" << B.transpose() << std::endl;
std::cout << "The A inverse is:\n" << A.inverse() << std::endl;
std::cout << "The determinant of A is:\n" << A.determinant() << std::endl;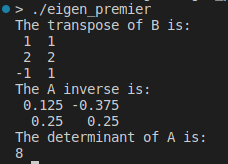

逆向、转置和行列式是实现我们的模型的基础。另一个关键点是将函数应用于矩阵的每个元素：

auto my_func = [](double x){return x * x;};
std::cout << A.unaryExpr(my_func) << std::endl;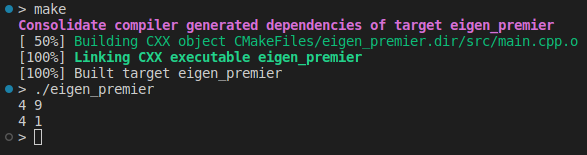

上面的例子可以在这里找到。

六、关于矢量化的一句话

        现代编译器和计算机体系结构提供了称为矢量化的增强功能。简而言之，矢量化允许使用多个寄存器并行执行独立的算术运算。例如，以下 for 循环：

for (int i = 0; i < 1024; i++) 
{
    A[i] = A[i] + B[i];
}

        以静默方式替换为矢量化版本：

for（i=0; i < 512; i += 2） 
{ A[i] =
 A[i] + B[i];
A[i + 1] = A[i + 1] + B[i + 1 ];
}

        由编译器。诀窍是指令与指令同时运行。这是可能的，因为两条指令彼此独立，并且底层硬件具有重复的资源，即两个执行单元。A[i + 1] = A[i + 1] + B[i + 1]A[i] = A[i] + B[i]

        如果硬件有四个执行单元，编译器将按以下方式展开循环：

for（i=0; i < 256; i += 4） 
{ A[i] =
 A[i] + B[i] ;
A[i + 1] = A[i + 1] + B[i + 1]; 
 A[i + 2] = A[i + 2] + B[i + 2]; 
 A[i + 3] = A[i + 3] + B[i +  3];
}

        与原始版本相比，此矢量化版本使程序运行速度提高了 4 倍。值得注意的是，这种性能提升不会影响原始程序的行为。

        尽管矢量化是由编译器、操作系统和硬件在木头下执行的，但我们在编码时必须注意允许矢量化：

• 启用编译程序所需的矢量化标志
• 在循环开始之前，必须知道循环边界，动态或静态
• 循环体指令不应引用以前的状态。例如，诸如此类的事情可能会阻止矢量化，因为在某些情况下，编译器无法安全地确定在当前指令调用期间是否有效。A[i] = A[i — 1] + B[i]A[i-1]
• 循环体应由简单和直线代码组成。 还允许函数调用和先前矢量化的函数。但复杂的逻辑、子例程、嵌套循环和函数调用通常会阻止矢量化工作。inline

在某些情况下，遵循这些规则并不容易。考虑到复杂性和代码大小，有时很难说编译器何时对代码的特定部分进行了矢量化处理。

根据经验，代码越精简和直接，就越容易被矢量化。因此，使用 、、 和 STL 容器的标准功能表示更有可能被矢量化的代码。<numeric>algorithmfunctional

七、机器学习中的矢量化

        矢量化在机器学习中起着重要作用。例如，批次通常以矢量化方式处理，使具有大批次的火车比使用小批次（或不批处理）的火车运行得更快。

        由于我们的矩阵代数库详尽地使用了矢量化，因此我们通常将行数据聚合成批次，以便更快地执行操作。请考虑以下示例：

        与其在六个向量和一个向量中的每一个之间执行 6 个内积以获得 6 个输出 ， 等等，我们可以堆叠输入向量以挂载一个包含六行的矩阵并使用单个乘法运行一次。XiVY0Y1MmulmatY = M*V

        输出是一个向量。我们最终可以解绑它的元素以获得所需的 6 个输出值。Y

八、结论和下一步

        这是一个关于如何使用现代C++编写深度学习算法的介绍性演讲。我们涵盖了高性能机器学习程序开发中非常重要的方面，例如函数式编程、代数演算和矢量化。

        这里没有涉及现实世界 ML 项目的一些相关编程主题，例如 GPU 编程或分布式训练。我们将在以后的故事中讨论这些主题。

在下一个故事中，我们将学习如何编写2D卷积代码，这是深度学习中最基本的操作。

九、引用

C++参考资料

特征线性代数库

C++中的 Lambda 表达式

英特尔矢量化要点