一、说明

初学者文本：此文本需要入门级编程背景和对机器学习的基本了解。张量是在深度学习算法中表示数据的主要方式。它们广泛用于在算法执行期间实现输入、输出、参数和内部状态。

在这个故事中，我们将学习如何使用特征张量 API 来开发我们的C++算法。具体来说，我们将讨论：

什么是张量
如何在C++中定义张量
如何计算张量运算
张量约简和卷积

在本文的最后，我们将实现 Softmax 作为将张量应用于深度学习算法的说明性示例。

。

二、什么是张量？

张量是类似网格的数据结构，它概括了任意数量的轴的向量和矩阵的概念。在机器学习中，我们通常使用“维度”这个词而不是“轴”。张量不同维度的数量也称为张量秩：

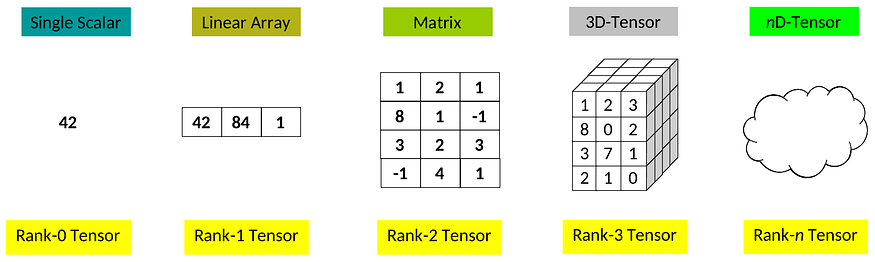
不同秩张量

在实践中，我们使用张量来表示算法中的数据，并用它们执行算术运算。

我们可以用张量执行的更简单的操作是所谓的元素级操作：给定两个具有相同维度的操作数张量，该操作会产生一个具有相同维度的新张量，其中每个系数的值是从操作数中各个元素的二进制评估中获得的：

系数乘法

上面的例子是两个 2 秩张量的系数乘积的图示。此操作对任何两个张量仍然有效，因为它们具有相同的维度。

像矩阵一样，我们可以使用张量执行其他更复杂的操作，例如矩阵类积、卷积、收缩、约简和无数的几何运算。在这个故事中，我们将学习如何使用特征张量 API 来执行其中一些张量操作，重点介绍对深度学习算法实现最重要的操作。

三、如何在C++中声明和使用张量

众所周知，本征是一个广泛用于矩阵计算的线性代数库。除了众所周知的对矩阵的支持之外，Eigen 还有一个（不支持的）张量模块。

虽然 Eigen Tensor API 表示不受支持，但它实际上得到了 Google TensorFlow 框架开发人员的良好支持。

我们可以使用特征轻松定义张量：

#include <iostream>

#include <unsupported/Eigen/CXX11/Tensor>

int main(int, char **)
{

    Eigen::Tensor<int, 3> my_tensor(2, 3, 4);
    my_tensor.setConstant(42);

    std::cout << "my_tensor:\n\n" 
              << my_tensor << "\n\n";

    std::cout << "tensor size is " << my_tensor.size() << "\n\n"; 

    return 0;
}

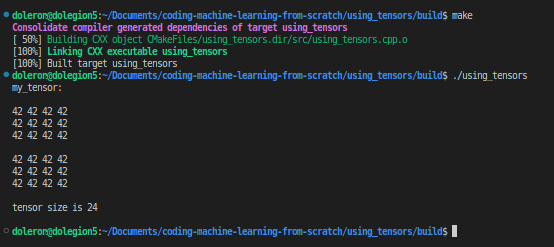
该行

Eigen::Tensor<int, 3> my_tensor(2, 3, 4);

创建一个张量对象并分配存储整数所需的内存。在此示例中，是一个 3 秩张量，其中第一维的大小为 2，第二维的大小为 3，最后一维的大小为 4。我们可以表示如下：2x3x4my_tensormy_tensor

如果需要，我们可以设置张量数据：

my_tensor.setValues({{{1, 2, 3, 4}, {5, 6, 7, 8}}});

std::cout << "my_tensor:\n\n" << my_tensor << "\n\n";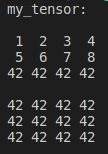

或改用随机值。例如，我们可以做：

Eigen::Tensor<float, 2> kernel(3, 3);
kernel.setRandom();
std::cout << "kernel:\n\n" << kernel << "\n\n";

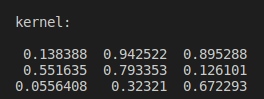
并在以后使用此内核来执行卷积。我们将很快在这个故事中介绍卷积。首先，让我们学习如何使用TensorMaps。

四、使用 Eigen：：TensorMap 创建张量视图

有时，我们分配了一些数据，只想使用张量来操作它。类似于但是，它不是分配新数据，而只是作为参数传递的数据的视图。检查以下示例：Eigen::TensorMapEigen::Tensor

//an vector with size 12
std::vector<float> storage(4*3);

// filling vector from 1 to 12
std::iota(storage.begin(), storage.end(), 1.);

for (float v: storage) std::cout << v << ','; 
std::cout << "\n\n";

// setting a tensor view with 4 rows and 3 columns
Eigen::TensorMap<Eigen::Tensor<float, 2>> my_tensor_view(storage.data(), 4, 3);

std::cout << "my_tensor_view before update:\n\n" << my_tensor_view << "\n\n";

// updating the vector
storage[4] = -1.;

std::cout << "my_tensor_view after update:\n\n" << my_tensor_view << "\n\n";

// updating the tensor
my_tensor_view(2, 1) = -8;

std::cout << "vector after two updates:\n\n";
for (float v: storage) std::cout << v << ','; 
std::cout << "\n\n";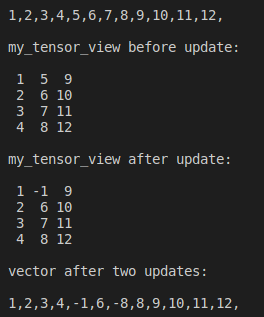

在这个例子中，很容易看出（默认情况下）特征张量 API 中的张量是 col-major。col-major和row-major是指网格数据如何存储在线性容器中的方式（查看维基百科上的这篇文章）：

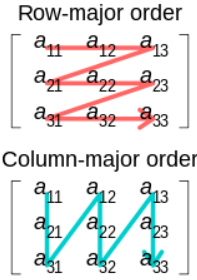
源

虽然我们可以使用行大张量，但不建议这样做：

目前仅完全支持默认列主布局，因此目前不建议尝试使用行主布局。

Eigen::TensorMap非常有用，因为我们可以使用它来节省内存，这对于深度学习算法等高要求的应用程序至关重要。

五、执行一元和二进制操作

特征张量 API 定义了常见的算术重载运算符，这使得对张量进行编程非常直观和直接。例如，我们可以加减张量：

Eigen::Tensor<float, 2> A(2, 3), B(2, 3);
A.setRandom();
B.setRandom();

Eigen::Tensor<float, 2> C = 2.f*A + B.exp();

std::cout << "A is\n\n"<< A << "\n\n";
std::cout << "B is\n\n"<< B << "\n\n";
std::cout << "C is\n\n"<< C << "\n\n";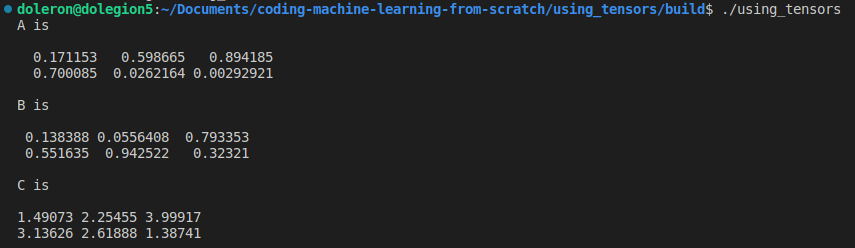

特征张量 API 还有其他几个元素级函数，如、和。此外，我们可以按如下方式使用：.exp()sqrt()log()abs()unaryExpr(fun)

auto cosine = [](float v) {return cos(v);};
Eigen::Tensor<float, 2> D = A.unaryExpr(cosine);
std::cout << "D is\n\n"<< D << "\n\n";

同样，我们可以使用：binaryExpr

auto fun = [](float a, float b) {return 2.*a + b;};
Eigen::Tensor<float, 2> E = A.binaryExpr(B, fun);
std::cout << "E is\n\n"<< E << "\n\n";

六、惰性求值和 auto 关键字

开发Eigen Tensor API的Google工程师遵循了与Eigen库顶部相同的策略。这些策略之一，也可能是最重要的策略，是如何延迟计算表达式的方式。

惰性求值策略包括延迟表达式的实际求值，以便将多个链式表达式组合到一个优化的等效表达式中。因此，优化的代码不是逐步计算多个单独的表达式，而是只计算一个表达式，旨在利用最终的整体性能。

例如，如果和是张量，则表达式实际上并不计算 A 和 B 的总和。实际上，该表达式会产生一个知道如何计算的特殊对象。仅当将此特殊对象分配给实际张量时，才会执行实际操作。换句话说，在下面的语句中：ABA + BA + BA + B

auto C = A + B;

C不是实际结果，而只是一个知道如何计算的计算对象（确实是一个对象）。只有当分配给张量对象（类型、、等的对象）时，才会对其进行评估以提供正确的张量值：A + BEigen::TensorCwiseBinaryOpA + BCEigen::TensorEigen::TensorMapEigen::TensorRef

Eigen::Tensor<...> T = C;
std::cout << "T is " << T << "\n\n";

当然，这对于像这样的小型操作没有意义。但是，此行为对于长操作链非常有用，在这些操作链中，可以在实际评估之前优化计算。在简历中，作为一般准则，而不是编写这样的代码：A + B

Eigen::Tensor<...> A = ...;
Eigen::Tensor<...> B = ...;
Eigen::Tensor<...> C = B * 0.5f;
Eigen::Tensor<...> D = A + C;
Eigen::Tensor<...> E = D.sqrt();

我们应该编写这样的代码：

Eigen::Tensor<...> A = ...;
Eigen::Tensor<...> B = ...;
auto C = B * 0.5f;
auto D = A + C;
Eigen::Tensor<...> E = D.sqrt();

不同之处在于，在前者中，实际上是对象，而在后面的代码中，它们只是惰性计算操作。CDEigen::Tensor

在恢复中，最好使用惰性计算来评估长操作链，因为该链将在内部进行优化，最终导致更快的执行。

七、几何运算

几何运算会产生具有不同维度的张量，有时还会产生大小。这些操作的示例包括：、、、和。reshapepadshufflestridebroadcast

值得注意的是，特征张量 API 没有操作。不过，我们可以使用以下方法进行模拟：transposetransposeshuffle

auto transpose(const Eigen::Tensor<float, 2> &tensor) {
    Eigen::array<int, 2> dims({1, 0});
    return tensor.shuffle(dims);
}

Eigen::Tensor<float, 2> a_tensor(3, 4);
a_tensor.setRandom();

std::cout << "a_tensor is\n\n"<< a_tensor << "\n\n";
std::cout << "a_tensor transpose is\n\n"<< transpose(a_tensor) << "\n\n";

稍后，当我们讨论使用张量的示例时，我们将看到一些几何运算的示例。softmax

八、规约（reduce）

归约是一种特殊操作情况，它会导致张量的维数低于原始张量。减少的直观案例是：sum()maximum()

Eigen::Tensor<float, 3> X(5, 2, 3);
X.setRandom();

std::cout << "X is\n\n"<< X << "\n\n";

std::cout << "X.sum(): " << X.sum() << "\n\n";
std::cout << "X.maximum(): " << X.maximum() << "\n\n";

在上面的示例中，我们缩小了所有尺寸一次。我们还可以沿特定轴执行缩减。例如：

Eigen::array<int, 2> dims({1, 2});

std::cout << "X.sum(dims): " << X.sum(dims) << "\n\n";
std::cout << "X.maximum(dims): " << X.maximum(dims) << "\n\n";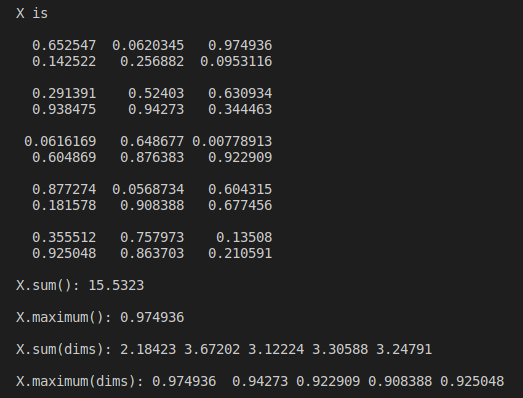

特征张量 API 具有一组预构建的归约操作，例如、、、等。如果任何预构建的操作不适合特定实现，我们可以使用提供自定义函子作为参数。prodanyallmeanreduce(dims, reducer)reducer

九、张量卷积

在前面的一个故事中，我们学习了如何仅使用普通C++和特征矩阵来实现 2D 卷积。事实上，这是必要的，因为在本征矩阵中没有内置的矩阵卷积。幸运的是，特征张量 API 有一个方便的函数来对特征张量对象执行卷积：

Eigen::Tensor<float, 4> input(1, 6, 6, 3);
input.setRandom();

Eigen::Tensor<float, 2> kernel(3, 3);
kernel.setRandom();

Eigen::Tensor<float, 4> output(1, 4, 4, 3);

Eigen::array<int, 2> dims({1, 2});
output = input.convolve(kernel, dims);

std::cout << "input:\n\n" << input << "\n\n";
std::cout << "kernel:\n\n" << kernel << "\n\n";
std::cout << "output:\n\n" << output << "\n\n";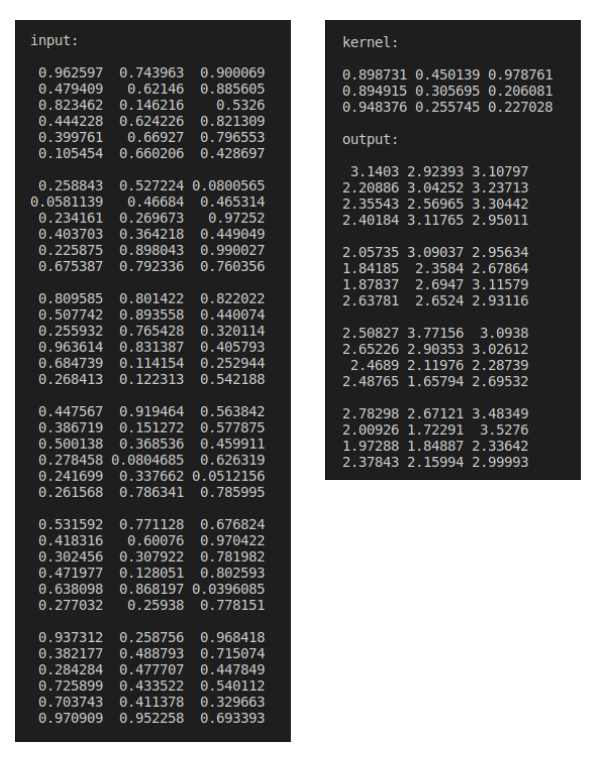

请注意，我们可以通过控制卷积中幻灯片的尺寸来执行 2D、3D、4D 等卷积。

十、带张量的软最大值

在编程深度学习模型时，我们使用张量而不是矩阵。事实证明，矩阵可以表示一个或最多二维网格，同时我们有更高维度的数据多通道图像或批量寄存器来处理。这就是张量发挥作用的地方。

让我们考虑以下示例，其中我们有两批寄存器，每批有 4 个寄存器，每个寄存器有 3 个值：

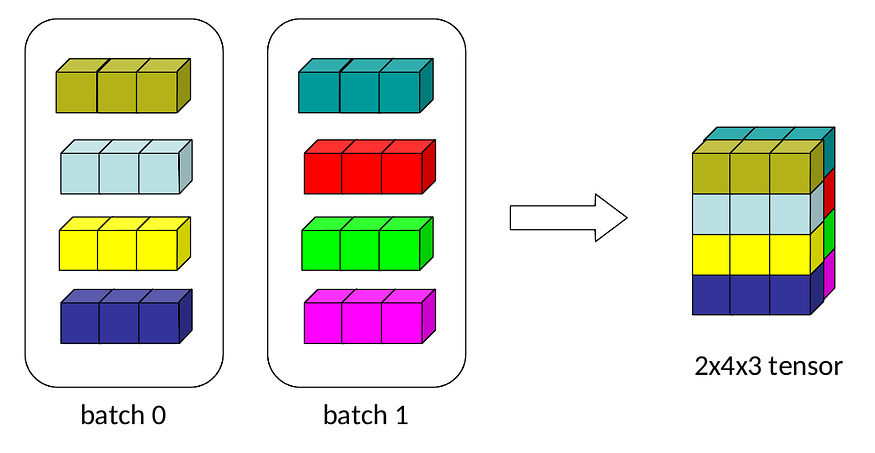
我们可以按如下方式表示这些数据：

Eigen::Tensor<float, 3> input(2, 4, 3);
input.setValues({
    {{0.1, 1., -2.},{10., 2., 5.},{5., -5., 0.},{2., 3., 2.}},
    {{100., 1000., -500.},{3., 3., 3.},{-1, 1., -1.},{-11., -0.2, -.1}}
});

std::cout << "input:\n\n" << input << "\n\n";

现在，让我们应用于此数据：softmax

Eigen::Tensor<float, 3> output = softmax(input);
std::cout << "output:\n\n" << output << "\n\n";

Softmax是一种流行的激活功能。我们在上一个故事中介绍了它的实现。现在，让我们介绍一下实现：Eigen::MatrixEigen::Tensor

#include <unsupported/Eigen/CXX11/Tensor>

auto softmax(const Eigen::Tensor<float, 3> &z)
{

    auto dimensions = z.dimensions();

    int batches = dimensions.at(0);
    int instances_per_batch = dimensions.at(1);
    int instance_length = dimensions.at(2);

    Eigen::array<int, 1> depth_dim({2});
    auto z_max = z.maximum(depth_dim);

    Eigen::array<int, 3> reshape_dim({batches, instances_per_batch, 1});
    auto max_reshaped = z_max.reshape(reshape_dim);

    Eigen::array<int, 3> bcast({1, 1, instance_length});
    auto max_values = max_reshaped.broadcast(bcast);

    auto diff = z - max_values;

    auto expo = diff.exp();
    auto expo_sums = expo.sum(depth_dim);
    auto sums_reshaped = expo_sums.reshape(reshape_dim);
    auto sums = sums_reshaped.broadcast(bcast);
    auto result = expo / sums;

    return result;
}

此代码输出：

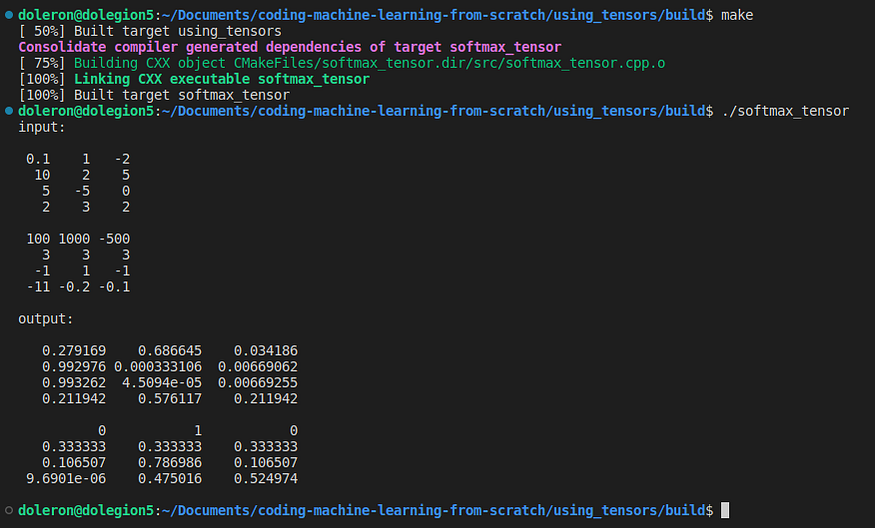
我们不会在这里详细介绍 Softmax。如果您需要查看Softmax算法，请不要犹豫，在Medium上再次阅读之前的故事。现在，我们只专注于了解如何使用特征张量来编码我们的深度学习模型。

首先要注意的是，该函数实际上并没有计算参数的softmax值。实际上，只挂载一个可以计算softmax的复杂对象。softmax(z)zsoftmax(z)

仅当的结果分配给类似张量的对象时，才会评估实际值。例如，在这里：softmax(z)

Eigen::Tensor<float, 3> output = softmax(input);

在这一行之前，一切都只是softmax的计算图，希望得到优化。发生这种情况只是因为我们在的正文中使用了关键字。因此，特征张量 API 可以优化使用更少操作的整个计算，从而改善处理和内存使用。autosoftmax(z)softmax(z)

在结束这个故事之前，我想指出和呼吁：tensor.reshape(dims)tensor.broadcast(bcast)

Eigen::array<int, 3> reshape_dim({batches, instances_per_batch, 1});
auto max_reshaped = z_max.reshape(reshape_dim);

Eigen::array<int, 3> bcast({1, 1, instance_length});
auto max_values = max_reshaped.broadcast(bcast);

reshape(dims)是一种特殊的几何运算，它生成另一个张量，其大小与原始张量相同，但尺寸不同。重塑不会在张量内部更改数据的顺序。例如：

Eigen::Tensor<float, 2> X(2, 3);
X.setValues({{1,2,3},{4,5,6}});

std::cout << "X is\n\n"<< X << "\n\n";

std::cout << "Size of X is "<< X.size() << "\n\n";

Eigen::array<int, 3> new_dims({3,1,2});
Eigen::Tensor<float, 3> Y = X.reshape(new_dims);

std::cout << "Y is\n\n"<< Y << "\n\n";

std::cout << "Size of Y is "<< Y.size() << "\n\n";

Note that, in this example, the size of X and Y is either 6 although they have very different geometry.

tensor.broadcast(bcast) repeats the tensor as many times as provided in the parameter for each dimension. For example:bcast

Eigen::Tensor<float, 2> Z(1,3);
Z.setValues({{1,2,3}});
Eigen::array<int, 2> bcast({4, 2});
Eigen::Tensor<float, 2> W = Z.broadcast(bcast);

std::cout << "Z is\n\n"<< Z << "\n\n";
std::cout << "W is\n\n"<< W << "\n\n";

不同的，不会改变张量秩（即维数），而只会增加维数的大小。reshapebroadcast

十一、局限性

特征张量 API 文档引用了一些我们可以意识到的限制：

GPU 支持经过测试并针对浮点类型进行了优化。即使我们可以声明，在使用 GPU 时也不鼓励使用非浮点张量。Eigen::Tensor<int,...> tensor;
默认布局（col-major）是唯一实际支持的布局。至少现在我们不应该使用行专业。
最大尺寸数为 250。只有在使用 C++11 兼容的编译器时才能实现此大小。