题面

题目描述

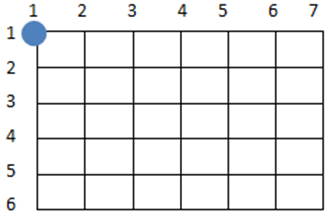
在一张n×m 的棋盘上（如 6 行 7 列）的最左上角(1,1) 的位置有一个卒。该卒只能向下或者向右走，且卒采取的策略是先向下，下边走到头就向右，请问从(1,1) 点走到 (n,m) 点可以怎样走，输出这些走法。

输入

两个整数n，m 代表棋盘大小（3≤n≤8,3≤m≤8）

输出

卒的行走路线。

样例

输入

复制

3 3

输出

复制

1:1,1->2,1->3,1->3,2->3,3
2:1,1->2,1->2,2->3,2->3,3
3:1,1->2,1->2,2->2,3->3,3
4:1,1->1,2->2,2->3,2->3,3
5:1,1->1,2->2,2->2,3->3,3
6:1,1->1,2->1,3->2,3->3,3

 链接

先深搜到终点输出在return回去

解法一：函数包含三个参数X，Y，K 

#include <bits/stdc++.h>
using namespace std;
int n , m , c = 0 , r[20][3];
int fx[3] = {0 , 1 , 0} , fy[3] = {0 , 0 , 1};
void print(int k){
	c++;
	printf("%d:" , c);
	for ( int i = 1 ; i < k ; i++ )
		printf("%d,%d->" ,  r[i][1] , r[i][2]);
	printf("%d,%d" , n , m);
	printf("\n");
}
void dfs( int x , int y , int k){
	r[k][1] = x;
	r[k][2] = y;
	if(x == n && y == m){
		print(k);
		return;
	}
	int tx , ty;
	for ( int i = 1 ; i <= 2 ; i++ ){
		tx = x + fx[i];
		ty = y + fy[i];
		if(tx >= 1 && tx <= n && ty >= 1 && ty <= m )
			dfs(tx , ty , k+1);
	}
}
int main(){
	scanf("%d%d" , &n , &m);
	dfs(1,1,1);
	return 0;
}

解法二：直接用r数组里存的元素

#include <bits/stdc++.h>
using namespace std;
int n , m , c = 0 , r[20][3];
int fx[3] = {0 , 1 , 0} , fy[3] = {0 , 0 , 1};
void print(int k){
	c++;
	printf("%d:" , c);
	for ( int i = 1 ; i < k ; i++ )
		printf("%d,%d->" ,  r[i][1] , r[i][2]);
	printf("%d,%d" , n , m);
	printf("\n");
}
void dfs(int k){
	int tx , ty;
	for ( int i = 1 ; i <= 2 ; i++ ){
		tx = r[k-1][1] + fx[i];
		ty = r[k-1][2] + fy[i];
		if(tx >= 1 && tx <= n && ty >= 1 && ty <= m ){
			r[k][1] = tx;
			r[k][2] = ty;
			if(tx == n && ty == m) print(k);
			else dfs(k+1);
		}
	}
}
int main(){
	scanf("%d%d" , &n , &m);
	r[1][1] = 1;
	r[1][2] = 1;
	dfs(2);
	return 0;
}